线段树
洛谷上有两道线段树模板(指模板1,模板2)都是区间维护的,也就是说,都离不开lasytag的维护,为了提高效率,故使用了lasytag,这里看一下题
【模板】线段树 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 k k k。
- 求出某区间每一个数的和。
输入格式
第一行包含两个整数 n , m n, m n,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 m m m 行每行包含 3 3 3 或 4 4 4 个整数,表示一个操作,具体如下:
1 x y k:将区间 [ x , y ] [x, y] [x,y] 内每个数加上 k k k。2 x y:输出区间 [ x , y ] [x, y] [x,y] 内每个数的和。
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
样例输出 #1
11
8
20
提示
对于 30 % 30\% 30% 的数据: n ≤ 8 n \le 8 n≤8, m ≤ 10 m \le 10 m≤10。
对于 70 % 70\% 70% 的数据: n ≤ 10 3 n \le {10}^3 n≤103, m ≤ 10 4 m \le {10}^4 m≤104。
对于 100 % 100\% 100% 的数据: 1 ≤ n , m ≤ 10 5 1 \le n, m \le {10}^5 1≤n,m≤105。
保证任意时刻数列中所有元素的绝对值之和 ≤ 10 18 \le {10}^{18} ≤1018。
【样例解释】
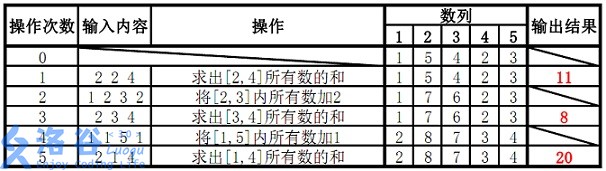
分析1.1
操作很少,只有:
- 区间加
- 区间求和
我们用数组存储线段树每个节点的状态即可,看代码:
代码1
#include <bits/stdc++.h>
using namespace std;
const int M = 1e5+10;
#define int long long
int a[M];
struct segment {
#define lc(p) (p<<1)
#define rc(p) ((p<<1)|1)int tag[M << 2], sum[M << 2];void f(int o, int l, int r, int k) {tag[o] += k;sum[o] += k * (r - l + 1);}void push_up(int x) {sum[x] = sum[lc(x)] + sum[rc(x)];}void push_down(int o, int l, int r) {int mid = l + r >> 1;f(lc(o), l, mid, tag[o]);f(rc(o), mid + 1, r, tag[o]);tag[o] = 0;}void build(int o, int l, int r) {if (l == r) { sum[o] = a[l]; return; }int mid = l + r >> 1;build(lc(o), l, mid);build(rc(o), mid + 1, r);push_up(o);}int query(int ql, int qr, int o, int l, int r) {if (l>qr or r<ql) return 0;if (ql <= l and r <= qr) return sum[o];int ans = 0;int mid = l + r >> 1;push_down(o, l, r);ans += query(ql, qr, lc(o), l, mid);ans+=query(ql,qr,rc(o),mid+1,r);return ans;}void update(int ql,int qr,int o,int l,int r,int k){if (l>qr or r<ql) return;if(ql<=l and r<=qr) {f(o,l,r,k);return;}push_down(o,l,r);int mid = l + r >> 1;update(ql, qr, lc(o), l, mid,k);update(ql,qr,rc(o),mid+1,r,k);push_up(o);}
}t1;
signed main() {int n,m;cin >> n>>m;for (int i = 1; i <= n; i++) cin >> a[i];t1.build(1,1,n);for (int i=1;i<=m;i++){int x,y,k;cin>>x;if (x==1){cin>>x>>y>>k;t1.update(x,y,1,1,n,k);}else{cin>>x>>y;cout<<t1.query(x,y,1,1,n)<<endl;}}return 0;
}分析1.2
我们只需要理解segment结构体
- sum[i]表示线段树第i个节点对应的区间和
- tag[i]就是节点i的懒标记
所以我们需要一个函数来标记节点,并修改此节点的和
void f(int o, int l, int r, int k) {tag[o] += k;sum[o] += k * (r - l + 1);}
f函数可以做到,它可以保存标记,并区间修改
当然标记需要下传,修改子节点后,父节点也要改变:
void push_up(int x) {sum[x] = sum[lc(x)] + sum[rc(x)];}
push_up可以重新求父节点的值
void push_down(int o, int l, int r) {int mid = l + r >> 1;f(lc(o), l, mid, tag[o]);f(rc(o), mid + 1, r, tag[o]);tag[o] = 0;}
push_down可以下传标记
而查询与更新只要递归查询,合并答案即可
【模板】线段树 2
题目描述
如题,已知一个数列,你需要进行下面三种操作:
- 将某区间每一个数乘上 x x x;
- 将某区间每一个数加上 x x x;
- 求出某区间每一个数的和。
输入格式
第一行包含三个整数 n , q , m n,q,m n,q,m,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 q q q 行每行包含若干个整数,表示一个操作,具体如下:
操作 1 1 1: 格式:1 x y k 含义:将区间 [ x , y ] [x,y] [x,y] 内每个数乘上 k k k
操作 2 2 2: 格式:2 x y k 含义:将区间 [ x , y ] [x,y] [x,y] 内每个数加上 k k k
操作 3 3 3: 格式:3 x y 含义:输出区间 [ x , y ] [x,y] [x,y] 内每个数的和对 m m m 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 3 3 3 的结果。
样例 #1
样例输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
样例输出 #1
17
2
提示
【数据范围】
对于 30 % 30\% 30% 的数据: n ≤ 8 n \le 8 n≤8, q ≤ 10 q \le 10 q≤10。
对于 70 % 70\% 70% 的数据:$n \le 10^3 , , ,q \le 10^4$。
对于 100 % 100\% 100% 的数据: 1 ≤ n ≤ 1 0 5 1 \le n \le 10^5 1≤n≤105, 1 ≤ q ≤ 1 0 5 1 \le q \le 10^5 1≤q≤105。
除样例外, m = 571373 m = 571373 m=571373。
(数据已经过加强 _)
样例说明:
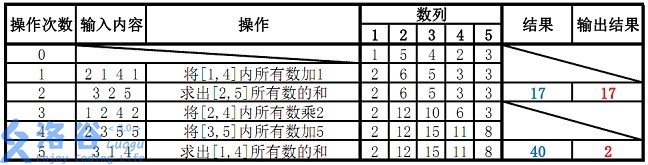
故输出应为 17 17 17、 2 2 2( 40 m o d 38 = 2 40 \bmod 38 = 2 40mod38=2)。
分析2
多了个乘法,再开数组代码逻辑会乱一点,但开个结构体即可:
struct node{int sum,mul,add;
};
不难想到,sum为区间和,mul为乘法懒标记,add为加法懒标记,对于一个区间x,可以存在子节点y,y应该接受懒标记:
y s u m = ( y s u m ∗ x m u l ) + x a d d ∗ ( y r − y l + 1 ) y_{sum}=(y_{sum}*x_{mul})+x_{add}*(y_r-y_l+1) ysum=(ysum∗xmul)+xadd∗(yr−yl+1)
修改y的懒标记:
y m u l = y m u l ∗ x m u l y_{mul}=y_{mul}*x_{mul} ymul=ymul∗xmul
y a d d = y a d d ∗ x m u l + x a d d y_{add}=y_{add}*x_{mul}+x_{add} yadd=yadd∗xmul+xadd
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define rc(x) ((x<<1)|1)
#define lc(x) (x<<1)
const int M = 1e6;
const int N=1e18;
int a[M],n,m,mod;
void read(){cin>>n;cin>>m>>mod;for (int i=1;i<=n;i++) cin>>a[i];
}
struct node{int sum,mul,add;
};
struct segment{node seg[M<<2];void push_up(int x){seg[x].sum=seg[lc(x)].sum+seg[rc(x)].sum;}void build(int o,int l,int r){seg[o].mul=1;seg[o].add=0;if (l==r){seg[o].sum=a[l];return;}int mid=(l+r)>>1;build(lc(o),l,mid);build(rc(o),mid+1,r);push_up(o);}void f(int o,int l,int r,int add,int mul){seg[o].mul=(seg[o].mul*mul)%mod;seg[o].add=(seg[o].add*mul)%mod;seg[o].add=(seg[o].add+add)%mod;seg[o].sum=(seg[o].sum*mul)%mod;seg[o].sum=(seg[o].sum+(r-l+1)*add)%mod;}void push_down(int o,int l,int r){int mid=(l+r)>>1;f(lc(o),l,mid,seg[o].add,seg[o].mul);f(rc(o),mid+1,r,seg[o].add,seg[o].mul);seg[o].add=0;seg[o].mul=1;}void update(int ql,int qr,int add,int mul,int o=1,int l=1,int r=n){if (ql<=l and r<=qr) {f(o,l,r,add,mul);return;}int mid=(l+r)>>1;push_down(o,l,r);if(ql<=mid) update(ql,qr,add,mul,lc(o),l,mid);if(qr>=1+mid)update(ql,qr,add,mul,rc(o),mid+1,r);push_up(o);}int query(int ql,int qr,int o=1,int l=1,int r=n){if (ql<=l and r<=qr) return seg[o].sum;int mid=(l+r)>>1,ans=0;push_down(o,l,r);if (ql<=mid) ans=(ans+query(ql,qr,lc(o),l,mid))%mod;if (mid+1<=qr) ans=(ans+query(ql,qr,rc(o),mid+1,r))%mod;push_up(o);return ans;}
}T1;
void solve(){int opt,x,y,k;cin>>opt>>x>>y;switch(opt){case 1:{cin>>k;T1.update(x,y,0,k);break;}case 2:{cin>>k;T1.update(x,y,k,1);break;}default:cout<<T1.query(x,y)<<endl;}
}
signed main(){ios::sync_with_stdio(false);read();T1.build(1,1,n);while(m--) solve();return 0;
}
与线段树1大致相同,不再过多赘述



分支)















