回归分析是统计学的核心。它其实是一个广义的概念,指那些用一个或多个预测变量来预测响应变量的方法。通常,回归分析可以用来挑选与响应变量相关的解释变量,可以描述两者的关系,也可以生成一个等式,通过解释变量来预测响应变量。
下面介绍如何用R函数拟合OLS回归模型、评价拟合优度、检验假设条件以及选择模型,为了能够恰当地解释OLS模型的系数,数据必须满足以下统计假设↓
正态性:对于固定的自变量值,因变量值成正态分布。
独立性:Yi值之间相互独立。
线性:因变量与自变量之间为线性相关。
同方差性:因变量的方差不随自变量的水平不同而变化。也可称作不变方差,但是说同方差性感觉上更犀利。
如果违背了以上假设,统计显著性检验结果和所得的置信区间就很可能不精确了。而现在机器学习中的回归都完全忽略了这一点,它认为现在的数据都是大数据了,其实,很多时候我们得到的不是所谓的大数据。
在R中,拟合线性模型最基本的函数就是lm(),格式为:
fit 其中,formula指要拟合的模型形式,data是一个数据框,包含了用于拟合模型的数据。结果对象存储在一个列表中,包含了所拟合模型的大量信息。
表达式(formula)形式如下↓
Y ~ X1 + X2 + ... + Xk
~ 左边为响应变量,右边为各个预测变量,预测变量之间用 + 符号分隔。
拟合模型后,将这些函数应用于lm()返回的对象,可以得到更多额外的模型信息。
summary():展示拟合模型的详细结果coefficients():列出拟合模型的模型参数(截距项和斜率)confint():提供模型参数的置信区间(默认95%)fitted():列出拟合模型的预测值residuals():列出拟合模型的残差值anova():生成一个拟合模型的方差分析表,或者比较两个或更多拟合模型的方差分析表vcov():列出模型参数的协方差矩阵AIC():输出赤池信息统计量plot():生成评价拟合模型的诊断图predict():用拟合模型对新的数据集预测响应变量值当回归模型包含一个因变量和一个自变量时,我们称为简单线性回归。
当只有一个预测变量,但同时包含变量的幂时,我们称为多项式回归。
当有不止一个预测变量时,则称为多元线性回归。
先从一个简单的线性回归例子开始,然后逐步展示多项式回归和多元线性回归↓
【简单线性回归】
数据准备,数据还是模拟电商的交易数据。
setwd("E:/R/基础/data")library(xlsx)df = read.xlsx("模拟相关数据.xlsx",1,encoding = "UTF-8")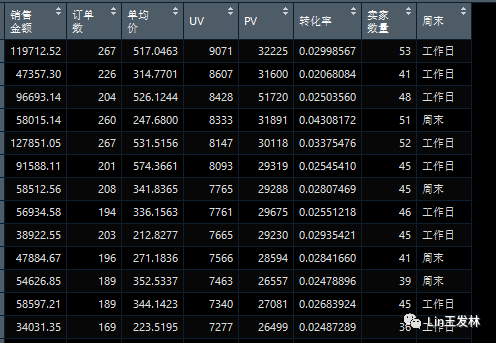
fit summary(fit)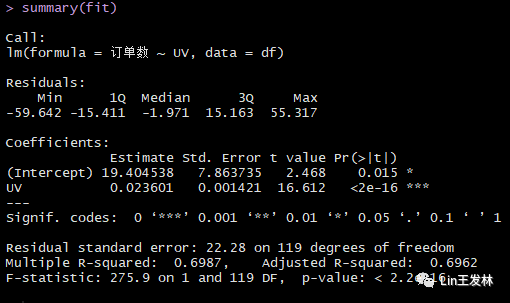
通过输出结果,可以得到预测等式:每日订单数=19.4+0.0236*每日UV数,相当于,每增加42个UV数,就能带来一个新的订单。因为没有用户登录就不可能有订单,所以没必要给截距项一个物理解释,它仅仅是一个常量调整项;在Pr(>|t|)栏,可以看到回归系数显著不为0(p<0.001);R平方项(0.6987)表明模型可以解释69.87%的方差,它也是实际和预测值之间相关系数的平方;
拟合模型的预测值
fitted(fit)
拟合模型的残差值
residuals(fit)
plot(df$UV,df$订单数, xlab="每日UV数", ylab="每日订单数")abline(fit,col='red',lwd=2)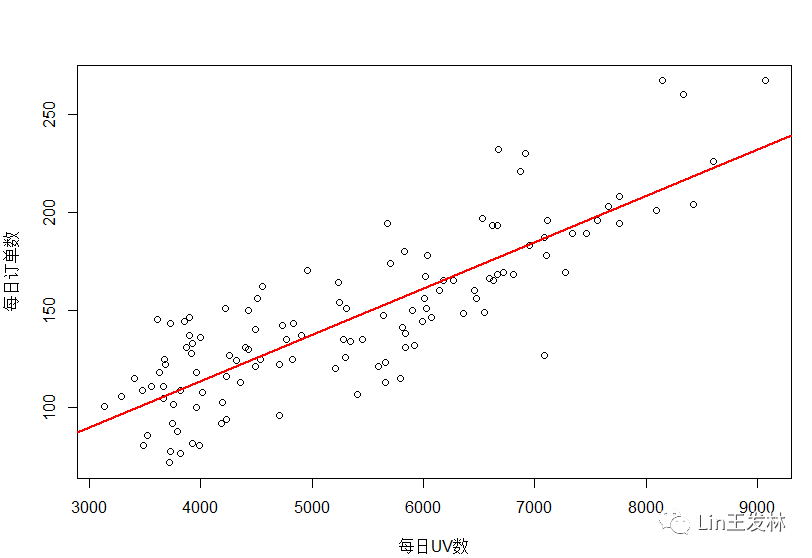
【多项式回归】
fit2 data=df)I(UV^3) 表示向预测等式添加一个UV的立方项。先试了一下平方项,发现3次项拟合效果更好。
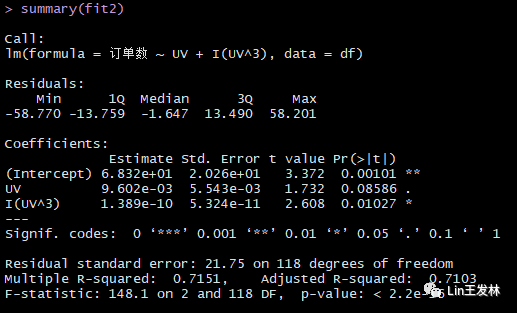
新的预测等式为:每日订单数=68.32+9.602e-03*每日UV数+1.389e-10*每日UV数的平方。
plot(df$UV,df$订单数, xlab="每日UV数", ylab="每日订单数")lines(df$UV,fitted(fit2),col='#0AC941',lwd=2)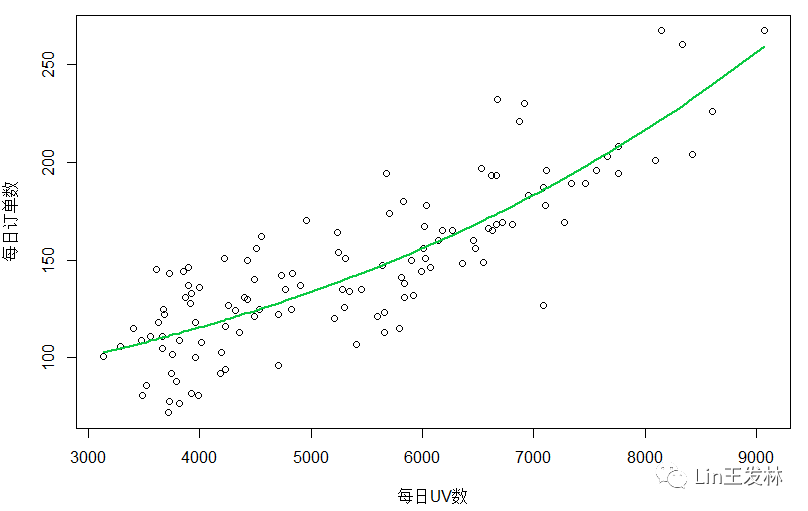
【多元线性回归】
当预测变量不止一个时,简单线性回归就变成了多元线性回归,分析也稍微复杂些。多元回归分析中,第一步最好检查一下变量间的相关性。cor()函数提供了二变量之间的相关系数,car包中scatterplotMatrix()函数则会生成散点图矩阵。scatterplotMatrix() 函数默认在非对角线区域绘制变量间的散点图,并添加平滑和线性拟合曲线。对角线区域绘制每个变量的密度图和轴须图。
df1 cor(df1)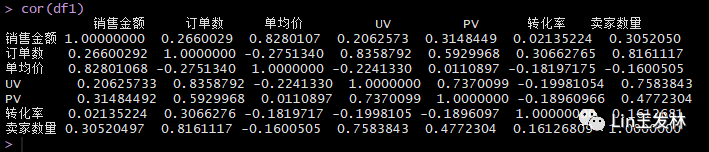
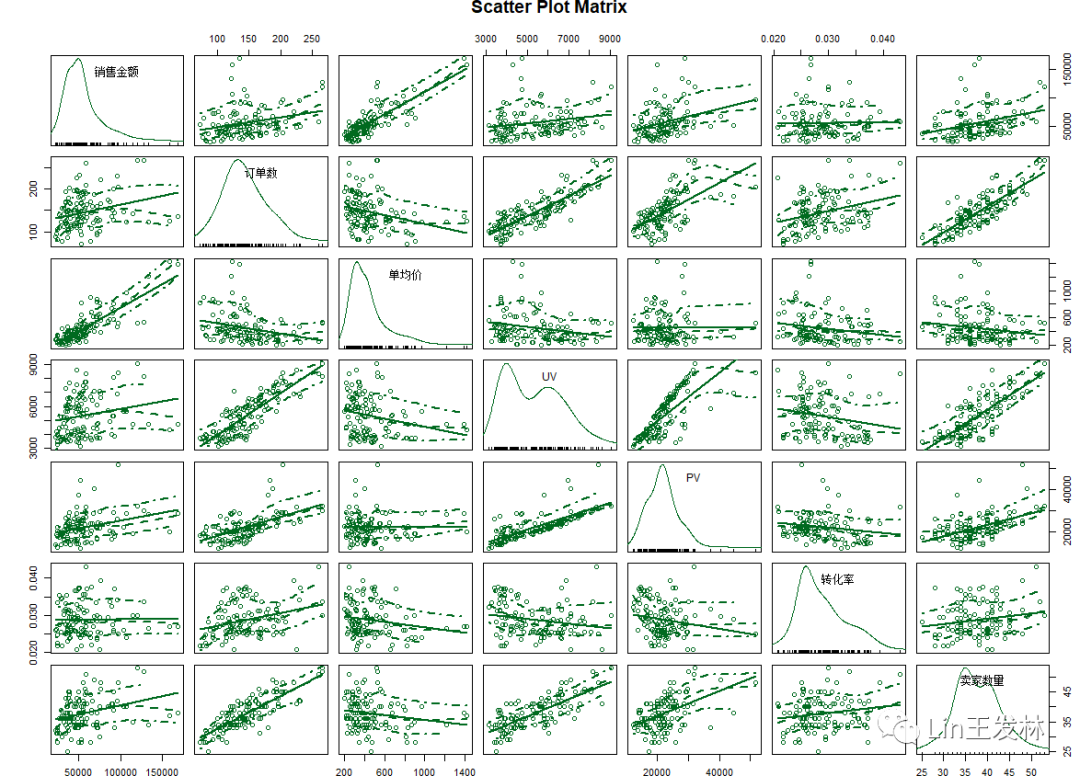
使用lm()函数拟合多元线性回归模型
fit data=df)summary(fit)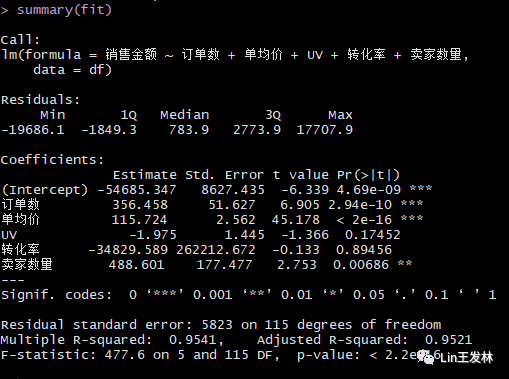
可以看到,影响销售金额的主要因素是订单数、单均价和卖家数量。而这里显示UV和转化率对销售金额影响不显著,这明显是不符合常理的。而UV和转化率对订单数影响很显著,然后通过订单数影响销售金额。
fit1 data=df)summary(fit1)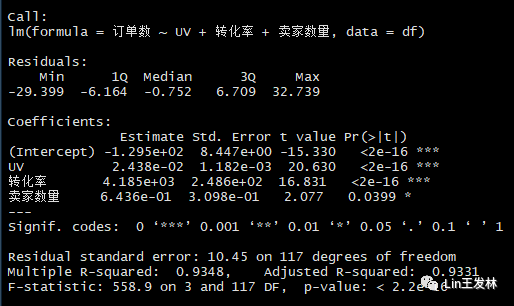
结果是这样↓
每增加一笔订单,金额增加356元;
单均价增加1元,金额增加116元;
卖家数量增加1家,金额增加489元。
卖家数量增加很难,就要想办法增加订单数和单均价,而订单数与UV和转化率关系很大,UV数每增加1000个,订单数可以增加24个,金额增加8544万元;而转化率每增加0.1%,订单数增加418笔。
所以拉新、留存很重要,运营也很重要。

End

之间(Integer. valueOf()方法))
)

)
:轻轻松松学SQL)



)





:初识Java内存模型)




