前言

这篇博客很久之前就想做了，一直在拖是因为觉得自己对知识点理解还没有足够的透彻。但是每当去复盘基本概念的时候又很难理清逻辑，所以觉得即便现在半吊子水平，但是也想通过博客记录一下自己肤浅的学习心得，权当是为自己巩固和梳理一遍知识点。

这篇博客主要借鉴了UCB的Pieter Abbeel大佬在youtube上的教学视频的思路，感兴趣的小伙伴可以移步这里 (国内的小伙伴可能需要借助一些魔法工具了hhh)，这个系列视频非常简短，只有六个视频，但是包含了大量的概念和理论推导，非常适合新手入门，和了解这个领域的一些基本概念，当你理清了这些基本概念再去看论文，就可以识别出来别人论文中一些新奇的概念是否来自于那些古老而优雅的数学推导了。

强化学习的本质

基本的神经网络学习目标是$max{\sum }_{i=0}^{\infty }P(y_i|x_i,\theta )$，其中$x_i$是输入的sample，$y_i$是对应的输出，NN的目标是学一个最优的参数$\theta$使得输入最优地映射为输出。

而强化学习的目标则解释为让智能体学会去做出一系列最优的决策，或者说让智能体学习到一个最优的策略，这个策略可以获得最大的折扣回报的期望。
$$Goal:\underset{\pi }{\max }E[\sum _{t=0}^H{\gamma }^t\cdot R(S_t,A_t,S_{t+1})|\pi ]\text{\hspace{1em}(1)}$$
其中，$\gamma$是折扣率，数值越大代表在计算折扣回报的时候越在意当前的动作对未来的影响。大写的$S,A$分别代表状态集合和动作集合。$\pi$代表策略函数。需要牢记上面的这个是期望折扣回报。

因为下面还要介绍一个概念叫做最优价值函数（Optimal Value Function，$V^{\ast }$），我们会发现强化学习中的这些新概念都是具有递进关系的，前面的那个期望折扣回报似乎是一个比较广泛的概念，它并没有限定在什么样的初始状态下开始进行序列决策，但是我们在进行游戏，或者在进行某一项任务的时候总是有一个初始状态的，所以对于我们来说，研究如何使用一个最优的策略函数去最大化给定初始状态的期望折扣回报更有意义，因此最优价值函数被定义为：expected sum of discounted rewards when starting from state $s$ and acting optimally:
$$V^{\ast }(s)=\underset{\pi }{\max }E[\sum _{t=0}^H{\gamma }^t\cdot R(S_t,A_t,S_{t+1})|\pi ,s_0=s]\text{\hspace{1em}(2)}$$
P.S.：这个函数的自变量是只有初始状态$s$。$\max$是为了acting optimally。

Value Iteration/价值迭代

“现在假设我们的状态空间是有限的，我们应该如何计算每种状态的最优价值函数呢？”

这是原始频的讲解中在这里提出的一个问题，但是在这之前我认为还缺少一个问题：

我们为什么要算每种状态的最优价值函数呢?

那显然是因为计算最优价值函数对我们是有帮助的，这个函数值代表的是某种状态下的期望折扣回报，所以在我们进行游戏或者某项任务的时候如果提前知道了这个环境中哪个状态的期望折扣回报最大或者比较大，那么我们在做动作的时候就可以倾向于让这些状态发生。比如下图的这种游戏：

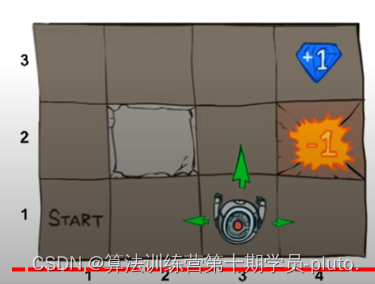
我们让机器人做动作，去吃到右上角的钻石。机器人位于不同的方格就是不同的状态，这个游戏中显然状态空间是有限的，那么如果我们知道机器人位于每个方格时的最优价值函数，那么我们就可以在做动作的时候让机器人尽量往数值大的方格上走。

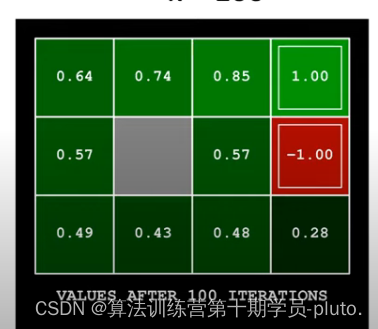
最终得到的最优价值函数可以用这个表格的方式展现出来，当我们处于不同的状态时，接下来应该向哪里走就显而易见了。

接下来，那我们就只需要看一下：

如何计算每种状态的最优价值函数呢？

第一个方法就是价值迭代法，公式如下：
$$V_{k+1}(s)=\underset{a}{\max }\sum _{s^{\prime }}P(s^{\prime }|s,a)(R(s,a,s^{\prime })+\gamma V_k(s^{\prime }))\text{\hspace{1em}(3)}$$
这里的公式大家可能会发现跟前面的公式有所出入，其实只是把期望给拆开了，这个公式里的求和符号替换之前的$E$，之前的求和符号隐含在迭代$\gamma V_k(s^{\prime })$之中。函数$V$的下标$k$就代表走了多少个时间步。当$k=0$的时候给定初始状态$s$，但是你一步也走不了，自然是没有reward的，所以$V_0(s)=0$。这样我们只要知道reward知道transition model也就是那个$P(s^{\prime }|s,a)$，我们就可以从$k=0$开始逐渐去求$k\to \infty$的时候价值函数的值，最终会收敛到最优价值函数的值。

所以对于一个有限状态空间和动作的强化学习任务我们可以使用下面这个伪代码展示的流程去解：

Start with V0(s)=0 for all s.For k=1,...,H:For all state s in S:Vk(s) <- max Equation (3)phai_k(s) <- argmax Equation (3)

通过价值迭代我们可以获得最终的最优价值函数以及每个状态相应的最优动作。需要注意的是这里的${\pi }^{\ast }(s)$针对每个状态s都是一个固定的动作，所以对于状态空间的探索是有限的。这种情况在探索小的状态空间的时候是没有问题的，因为总共穷举出来的轨迹也是有限的。

对上面这句话的一个直觉的解释：这里的轨迹就是从初始状态开始一直到最终游戏结束这个过程中智能体所做的所有动作，经历的所有状态和所有的rewards合并到一起就是一条轨迹，我们所说的智能体在学习，其实是让它在每条轨迹中学习到新的信息，一条轨迹对于智能体的训练来说是一个sample，更多的sample自然可以让智能体探索到更广泛的空间，学到的东西理论上也越多，而不会仅仅局限于某一种环境中。

讲述到这里其实价值迭代还差一步就是

为什么这个价值迭代一定会converge?

首先我们知道:
$V^{\ast }(s)=$expected sum of rewards accumulated starting from state $s$, acting optimally for $\infty$ steps.
$V_H(s)=$expected sum of rewards accumulated starting from state $s$, acting optimally for $H$ steps.
然后我们用下面的公式可以表示H之后收集的折扣奖励：
$r^{H+1}R(s_{H+1})+r^{H+2}R(s_{H+2})+...<=r^{H+1}{R}_{max}+r^{H+2}{R}_{max}+...=\frac{r_{H+1}}{1-r}{R}_{max}$

所以当$H\to \infty$的时候上面这个式子趋近于0，所以H之后时间步的累积折扣奖励趋近于0，那么$V_H(s)\to V^{\ast }(s)$。

总结

价值迭代法用于小范围state的策略探索。

Q-Value Iteration

前面讲到的最优价值函数的自变量只有一个状态，然后从这个状态开始acting optimally收集的折扣奖励作为最优价值。但是如果我们从状态s开始想尝试所有的动作，而不仅仅是尝试最优的动作（针对状态s作出的动作），这里我们就要把针对状态s作出的动作a假设为所有可能的动作，相当于我们对于每个状态不再只有一个最优价值函数，而是在该状态下每个动作都有一个价值函数，我们都可以求。

Q-value定义为：expected utility starting from s, taking action a, and (thereafter) acting optimally.

$$Q^{\ast }(s,a)=\sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{\max }{Q}^{\ast }(s^{\prime },a^{\prime })]\text{\hspace{1em}(4)}$$

相比于Optimal Value Function，Q-value可以通过相对更多的信息，比如给定一个状态及其q价值，那我们可以直接判断出那个动作下的q价值是最大的，直接作出动作。但是从价值函数是看不出来当前状态做哪个动作是最大的，你需要遍历所有的状态。

那么解决Q-value和证明其收敛性与之前的价值迭代是一样的这里不再给出具体的证明。
$$Q_{k+1}^{\ast }(s,a)\leftarrow \sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{\max }{Q}_k^{\ast }(s^{\prime },a^{\prime })]\text{\hspace{1em}(5)}$$

策略迭代法

前面说到价值迭代法在做游戏的时候想要从初始状态s产生一系列最优的动作的话需要遍历所有的状态，求出其最优价值函数。

为了进一步简化价值迭代法，我们又引入了q-value迭代法，q-value中引入了针对当前状态s所作的动作a作为额外的自变量，这样我们在给定状态s的时候，就可以从q(s,a)中找到最大的那个动作a作为最优策略。

这两个方法本质上是相同的，都是需要遍历所有的动作才能找到最大的那个价值，所以policy iteration提出是为了用迭代去替代遍历。

Policy iteration分为policy evaluation和policy improvement两步。其中evaluation步骤，我们用价值迭代得到当前策略下的价值函数，去评估当前的policy质量（policy evaluation）：
$$V_k^{\pi }(s)\leftarrow \sum _{s^{\prime }}P(s^{\prime }|s,\pi (s))[R(s,\pi (s),s^{\prime })+\gamma V_{k-1}^{\pi }(s^{\prime })]\text{\hspace{1em}(6)}$$
直到其收敛。

通过这个不太准确的“最优价值函数”，我们对policy进行更新 (policy improvement)：
$${\pi }_{k+1}(s)\leftarrow \underset{a}{\mathrm{argmax}}\sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma V^{{\pi }_k}(s^{\prime })]\text{\hspace{1em}(7)}$$
这个迭代是一定会收敛的，因为只要我们的迭代次数足够多，实际上每种策略我们都可以经历一遍，也就是说最终肯定会有${\pi }_{k+1}(s)={\pi }_{k}sforallstates$.

所以对于任意的s，我们都可以有：
$$V^{{\pi }_k}(s)=\underset{a}{\max }\sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma V^{{\pi }_k}(s^{\prime })]\text{\hspace{1em}(8)}$$
这就意味着收敛时的V正是最优价值函数。

总结

总结来说，价值迭代是在迭代迭代最优价值函数的时候就对所有的动作轨迹进行尝试，直接找到最准确的对于当前状态的最优价值函数。

而策略迭代则是每一次用不太准确的最优价值函数去更新策略，一步一步的逼近真正的最优价值函数，从而得到最优策略。

两者并没有本质的区别。

Model-free $\to$ Q-learning

之前介绍的两种方法价值迭代和策略迭代都属于model-based的方法，因为在他们的公式中都有$P(s^{\prime }|s,a)$这一项，这个转换模型在真实的任务中我们通常是未知的，不可以求解的。

此外，前面的两种方法还受限于小尺度的状态空间和动作空间。

因此我们现在多数用的还是model-free的方法。
回忆q-value的迭代中，我们使用的是下面这个公式
$$Q_{k+1}^{\ast }(s,a)\leftarrow \sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{\max }{Q}_k^{\ast }(s^{\prime },a^{\prime })]\text{\hspace{1em}(9)}$$
也可以写作，
$$Q_{k+1}^{\ast }(s,a)\leftarrow E_{s^{\prime }-P(s^{\prime }|s,a)}[R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{\max }{Q}_k^{\ast }(s^{\prime },a^{\prime })]\text{\hspace{1em}(10)}$$
这是在求一个期望，所以model-free的方法就是利用sample作为期望的估计以摆脱transition model的限制。

上面就是tabular的q-value的伪代码，简单来讲就是对每个状态都随机sample一个动作(采用$\delta$-greedy策略，也就概率发生随机采样和选取当前q-value下最优的动作)。

这里视频作者乘其为off-policy learning，我想就是这里的sample action是跟策略无关的sample，作者提到该方法可以可靠地收敛到最优的q-value，这个在理论上有原论文中两页纸的证明，视频中并没有进行讲解，我想暂时我也看不懂所以这边就当作结论线记下来。

此外，我们注意这段伪代码中的这个target其实比较熟悉，它其实就是我们之前提到过的用于更新价值网络的那个TD target，更新后的q-value就是为了更接近这个target。

但是上面这种方法只是解决了转换模型的限制，并没有适应更大的状态空间，因为它还是记录了所有状态下不同动作的q-value，所以它叫做tabular q-learning.

那么为了不用表格去存储q-value，有研究提出了parameterized Q function: $Q_{\theta }(s,a)$，也就是用参数$\theta$去"存储"所有的q值。
那么这里我们就从直接迭代优化q-value转变到了迭代优化参数$\theta$，但是注意的是这里的target我们仍然用的TD target：
$$target(s^{\prime })=R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{\max }{Q}_{{\theta }_k}(s^{\prime },a^{\prime })\text{\hspace{1em}(10)}$$
参数更新：
$${\theta }_{k+1}\leftarrow {\theta }_k-\alpha {\nabla }_{\theta }[\frac{1}{2}(Q_{\theta }(s,a)-target(s^{\prime }){)}^2]{|}_{\theta ={\theta }_k}\text{\hspace{1em}(11)}$$
上面这种方法其实就是DQN

这个图给了一个double DQN的伪代码，其基本原理其实跟前面的tabular Q-learning是一样的，只不过这里引入了经验回放和double Q network的机制。

经验回放

引入这个机制的原因其实我们可以通过对比之前tabular q-learning的伪代码的区别发现：之前的tabular模式下，每一次对Q-value的迭代是更新了所有的状态下的q值的。但是我们提出DQN就是为了解决大尺度状态空间下无法存储所有的Q-value的问题，所以自然我们不可能让所有的状态都参与到Q网络的参数更新中。

所有我们在迭代的时候会存储一些之前遇到过的transitions，就是图中的这个括号里的这些信息，它包括了从一个状态采取了一个动作然后切换到了下一个状态以及得到的奖励是多少，然后后面参数更新的时候使用一些之前的transitions。我们把之前经历的这些transitions称为经验。

还需要注意的一点是，这里用的是随机采样的一些经验去更新，而不是用前面连续几次的经验。这是因为连续的经验可能高度相关，我们要打破经验之间的关联性，避免数据过拟合某些经验，当然这只是其中一个原因。还有一个原因是作者认为之前的经验也存在价值，比如t=3时候的经验对于t=10的时候也是有价值的。

Double Q Network

而引入double q network的目的，在论文中解释为，为了避免q网络过渡估计的问题。
我们看上图的TD target的计算公式会发现其中的用的$Q^{-}$网络是比$Q$网络要“慢半拍”的。
因为如果某一条经验是有噪声的，就是不太好的经验导致Q网络更新了，那这个TD target中用Q网络得到的最优动作a显然是不太靠谱的，所以用两个Q网络，其中一个网络慢于另一个更新就可以一定程度上避免这种情况发生。

总结

关于q-learning比较有经典且代表性的算法就是DDQN。DDQN主要是学习一个Q网络，它的输入是当前状态和动作，输出是从当前状态开始，采取动作a之后的每一步都是optimal action的情况下所获得的折扣回报的期望，这个也是q-value的意义。网络的成本函数是缩小q-value和TD target之间的距离。

那么在训练结束后，我们就得到了最终的q function，那么在给定状态s之后，我们就可以计算那个q(s,a)是最大的从而找到针对当前状态的最优动作。

策略梯度算法

DQN通常被认为具有较高的数据效率但是训练不够稳定，并且最终确定动作用得是$\mathrm{argmax}$，这只能操作与离散的动作，对于连续的动作求极值很难。

因此研究人员想用一个简单的网络针对当下的状态直接输出动作，这个网络就叫做策略网络。
所以这个网络的输入就是当前状态，输出就是动作概率分布。

接下来我们来明确这个网络的成本函数：
假设让$\tau$代表一个state-action序列$s_0,u_0,...,s_H,u_H$
$R(\tau )={\sum }_{t=0}^{H}R(s_t,u_t)$这个代表这个序列的奖励总和，我们称之为一条轨迹的奖励总和。
然后我们引入策略网络的目标函数：
$U(\theta )=E({\sum }_{t=0}^{H}R(s_t,u_t);{\pi }_{\theta })$
其中${\pi }_{\theta }$代表策略网络，比如$u_0={\pi }_{\theta }(s_0)$，给定一个状态$s_0$产生一个动作$u_0$。
所以上面这个公式的含义就是在当前的策略网络参数下所有可能出现的轨迹的奖励总和的期望，也可以写成下面这个形式：
$U(\theta )={\sum }_{\tau }P(\tau ;\theta )R(\tau )$，其中$P(\tau ;\theta )$就是在当前的策略网络下出现轨迹$\tau$的概率。所以策略网络反映的动作概率分布产生的最优轨迹概率越高则我们的目标函数就会越大，所以我们期望更新参数$\theta$以最大化目标函数。

采用梯度算法更新参数：

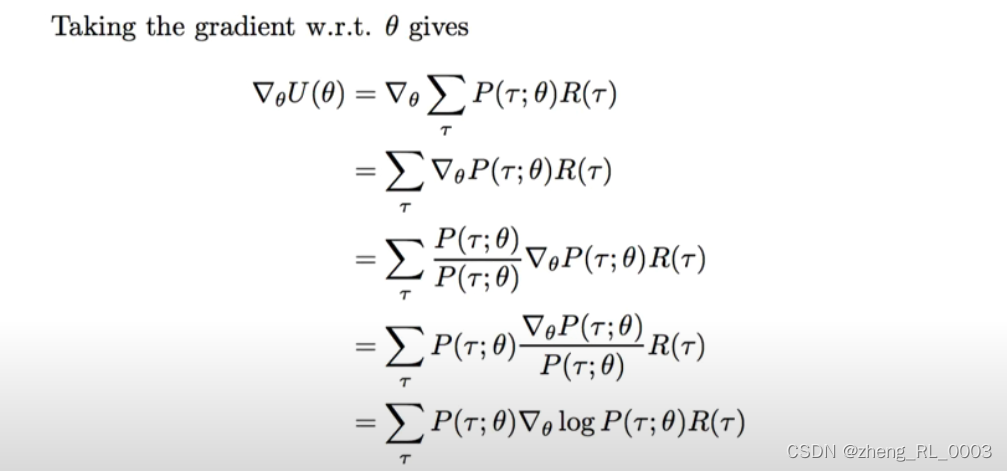
从最后的这个求梯度的公式来看，显然遍历所有的轨迹是不现实的，因此通常的做法是采用经验估计的方法去近似这个梯度，如下图所示，也就是随机挑选m条轨迹求平均。

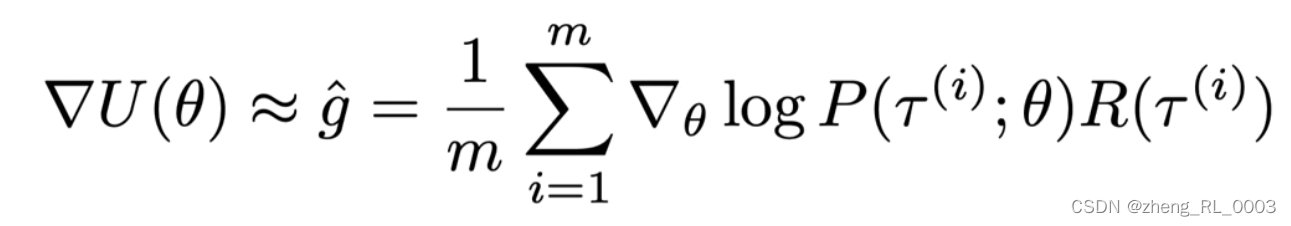
因为我们是最大化目标函数$U(\theta )$，所以使用梯度上升。那么这里的奖励R如果是大于0的，就相当于我们在提升一条带有好的奖励的轨迹，如果reward是小于0的，那么相当于把负的reward的轨迹的概率给降低。这是对这个策略梯度公式的直觉上的理解。

进一步的我们把梯度公式中的log部分拆开：

会发现最终梯度的计算跟transition model没有关系，因为我们是对参数求导而transition model与策略网络的参数无关，所以它的导数是0. 至此，我们明白了策略梯度算法为何属于model-free的方法。

error correct in the paper “Deep Progressive Reinforcement Learning for Skeleton-based Action Recognition”

这里我们把这个梯度带回我们目标函数的梯度公式中会发现会发现这个策略梯度公式跟上次汇报提到的策略梯度的形式很像，如下图是上次汇报中提到的那篇文章所用的策略梯度公式，我们忽略符号上的不一致，会发现差别其实只是在这篇论文中他在做经验估计的时候只用了一条轨迹，而我们前面推导的策略梯度是用了多条随机轨迹去做策略梯度的经验估计，所以它这里的公式12其实有一点问题，加号应该改成减号，正如它文字中所说的，它定义的loss function是带了负号的策略梯度，所以在参数更新公式中应该是梯度下降，这样才与通常策略梯度算法中的梯度上升是匹配的：

Baseline substraction and actor-critic

总结一下，策略网络以给定状态为输入，输出一个动作概率分布，训练的目标是找的一组参数$\theta$让这组参数下可以获得的不同轨迹的奖励总和的期望最大，就是让这组参数下最优轨迹的概率最大。而前面介绍的策略梯度理论上已经可以用来更新网络参数，使其实现预定的目标。但是后面还有了actor-critic的结构，也就是在策略网络的基础上引入了一个价值网络。

所以这一小节，我会推导从naive的策略梯度如何到了actor-critic，这里通过了一系列比较有意思的数学推导得到了最终的结果，但是在视频中并没有进行严格的推导，所以我这里也是讲解比较intuition层面的推导逻辑。

前面的这个策略梯度有两个问题，这个梯度是sample了一条轨迹或者几条轨迹算出来的，而不是一个期望，所以会引入noise，导致这样计算的梯度方差可能比较大，也就是说它计算的不准。
第二个问题是，前面我们在intuition的层面上对策略梯度进行的解释是：增加reward大于0的轨迹的概率，减小reward小于0的轨迹的概率。这样就引入一个问题，很有可能某些任务上我的reward是没有负值的，所以这样的策略梯度对于好的轨迹的提升或者对于坏的轨迹的抑制作用就不是很明显。所以能不能我对轨迹的奖励设置一个baseline，然后我去增加大于这个baseline的轨迹的概率，然后抑制小于这个baseline的轨迹的概率，所以如下图所示我们可以得到了新的策略梯度。对于第一个问题，从直觉上理解，我们让原始的reward减去了一个baseline b相当于减小了奖励的大小，一定程度上限制了梯度的方差。（当然这里应该有更严格的数学证明，但是视频中暂时没有讲。）

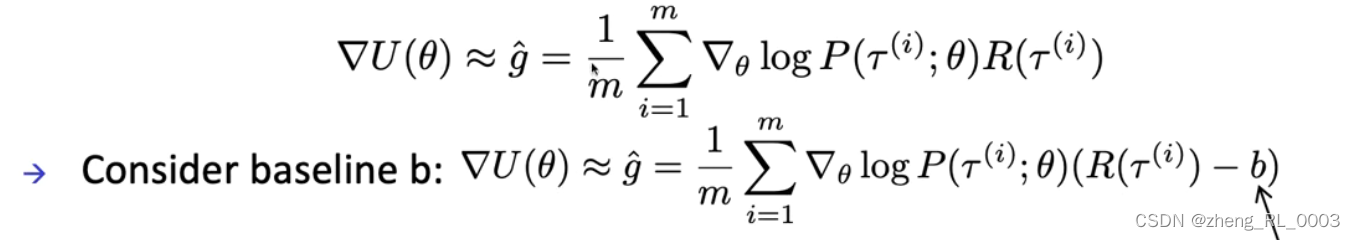
后面还有一步操作是移除与当前动作$u_t$无关的奖励项，这进一步缩小了奖励值所以进一步降低了梯度估计的方差。

然后我们发现下面这个公式的第一项有点像Q-value，差了个折扣率，那我们就加上折扣率，让它就边为q-value，这样括号里的值又减小了一些，那梯度估计的方差也可以变小一些。至于括号里的第二项，就更加明显了，这个就是value function价值函数。

总结一下，从基本的策略梯度到actor-critic主要经历了baseline的引入，引入baseline是为了让平均线以上的轨迹出现的概率更高同时抑制平均线一下的轨迹出现概率，避免出现奖励值只有大于0的情况下，基本的策略梯度会对所有轨迹都进行概率提升导致优秀的轨迹出现的不明显。此外，引入baseline还可以降低sample-based的策略梯度估计的方差。

引入baseline那么我们就要对baseline进行估计，这里的baseline不能与动作有关，所以baseline仅依赖与状态$s_t$，所以我们用价值函数充当baseline，然后把策略梯度括号里的这第一项进一步的用Q-value替代。所以我们需要一个额外的价值网络去估计价值函数，所以整个的带有价值网络的网络更新流程可以简述为下图。图中主要表示了价值网络的参数我们是通过TD target进行更新的，后面这一项是为了让更新前后的参数不要相差特别多。而策略网络的参数我们就通过前面推导的策略梯度进行更新。

TRPO