本文转自: 离散卷积与自相关----------信号处理系列 http://www.cnblogs.com/einyboy/archive/2012/12/30/2839633.html
一、 定义
离散信号f(n),g(n)的定义如下:

N-----为信号f(n)的长度
s(n)----为卷积结果序列,长度为len(f(n))+len(g(n))-1
以3个元素的信号为例:
f(n) = [1 2 3]; g(n) = [2 3 1];
s(0) = f(0)g(0-0) + f(1)g(0-1)+f(2)g(0-2) = 1*2 + 2*0 + 3*0 =2
s(1) = f(0)g(1-0) + f(1)g(1-1) + f(2)g(1-2) = 1*3 + 2*2 + 3*0 = 7
s(2) = f(0)g(2-0) + f(1)g(2-1) + f(2)g(2-2) =1*1 + 2*3 + 3*2=13
s(3) = f(0)g(3-0) + f(1)g(3-1) + f(2)g(3-2) =1*0 + 2*1 + 3*3=11
s(4) = f(0)g(4-0) + f(1)g(4-1) + f(2)g(4-2) =1*0 + 2*0 + 3*1=3
最终结果为:
s(n) = [2 7 13 11 3]
上述计算图示如下:
在数学里我们知道f(-x)的图像是f(x)对y轴的反转
g(-m)就是把g(m)的序列反转,g(n-m)的意义是把g(-m)平移的n点:

如上图g(m)在信号处理中通常叫做滤波器或掩码,卷积相当于掩码g(m)反转后在信号f(n)上平移求和。Matlab计算卷积的函数为conv,
>> A = [1 2 3];
B = [2,3,1];
convD = conv(A,B)
convD =
2 7 13 11 3
相应的二维卷积定义如下:
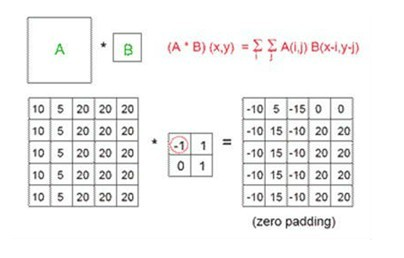
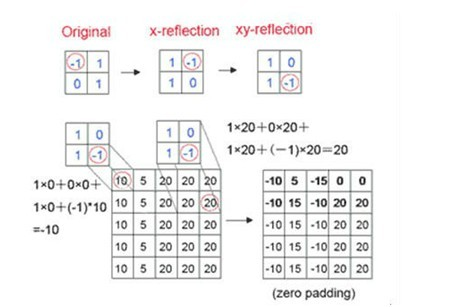


)
















