● 本文适合高二下学期、高三一轮复习的同学阅读。先看视频再看文字，看视频时注意利用暂停，想清楚每一步变形的依据。

01

曲边梯形的面积、微积分基本定理的内容

视频讲解

1、曲边梯形的概念及面积求法

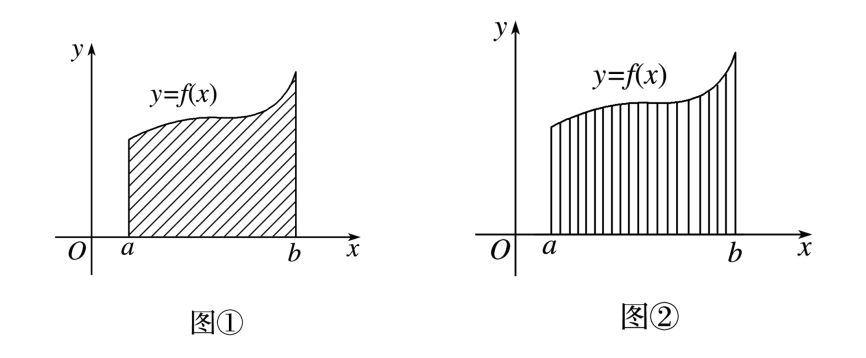
(1)曲边梯形：由直线x＝a，x＝b(a≠b)，y＝0和曲线y＝f(x)所围成的图形称为曲边梯形(如图①所示).

(2)求曲边梯形面积的方法：

把区间[a，b]分成许多小区间，进而把曲边梯形拆分为一些小曲边梯形.对每个小曲边梯形“以直代曲”，即用矩形的面积近似代替小曲边梯形的面积，得到每个小曲边梯形面积的近似值，对这些近似值求和，就得到曲边梯形面积的近似值(如图②所示).

(3)求曲边梯形面积的步骤：①分割；②近似代替；③求和；④取极限.。

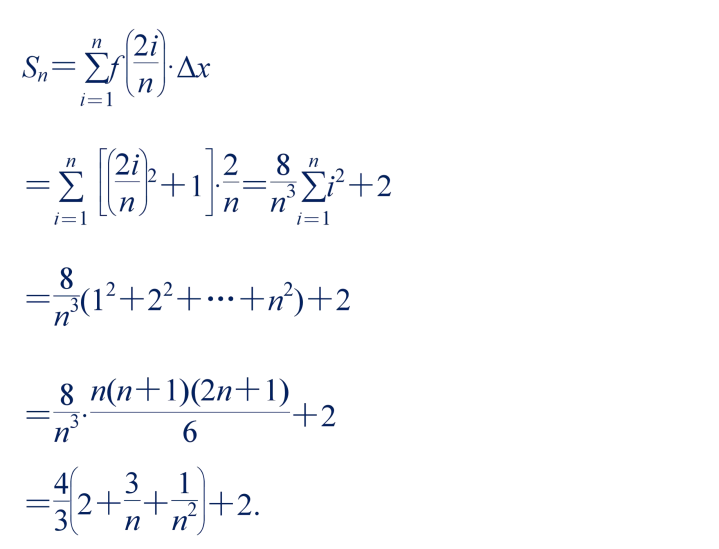
2、定积分的概念

3、定积分的几何意义

4、定积分的计算性质

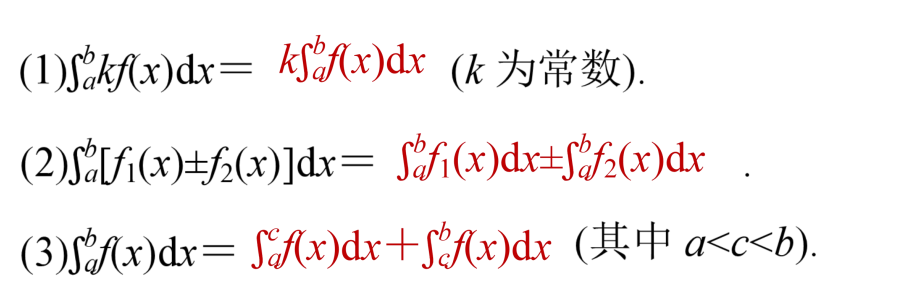
5、微积分基本定理

6、常用原函数与被积函数关系式

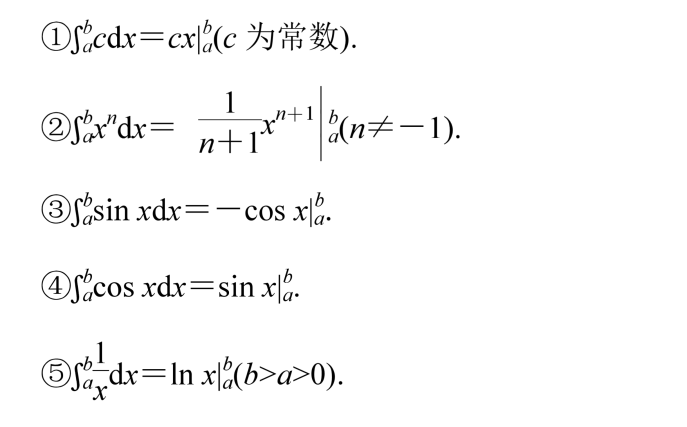
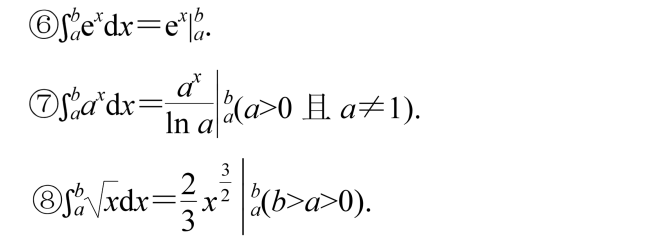
02

微积分基本定理运用、求封闭图形面积

视频讲解

7、根据积分几何意义求图形面积

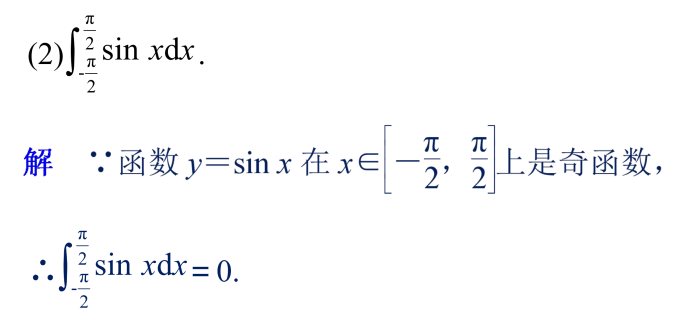
8、根据积分基本定理计算定积分

(1)当被积函数为两个函数的乘积或乘方形式时一般要转化为和的形式，便于求得原函数F(x).

(2)由微积分基本定理求定积分的步骤

第一步：求被积函数f(x)的一个原函数F(x)；

第二步：计算函数的增量F(b)－F(a).

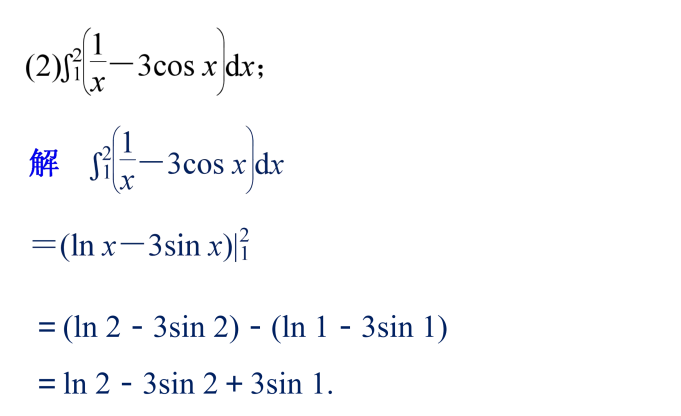
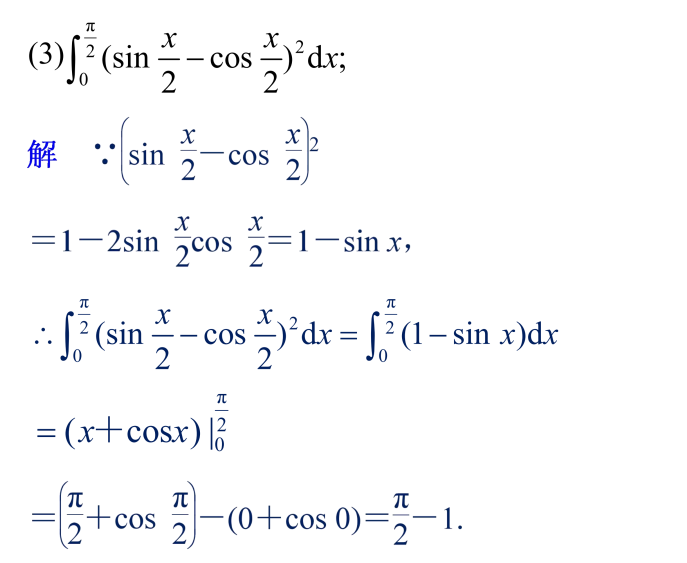
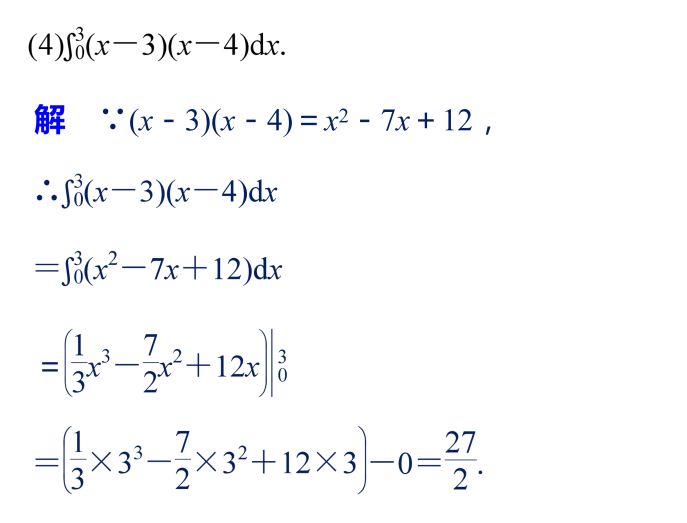
分段函数定积分的求法

(1)利用定积分的性质，转化为各区间上定积分的和计算。

(2)当被积函数含有绝对值时，常常去掉绝对值号，转化为分段函数的定积分再计算。

9、利用定积分求函数图像围成的图形面积

求由曲线围成的面积，要根据图形，确定积分上、下限，用定积分来表示面积，然后计算定积分即可。

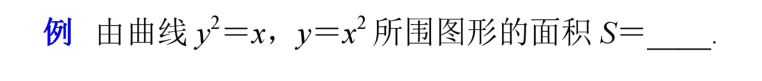
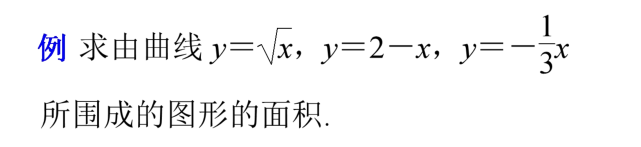
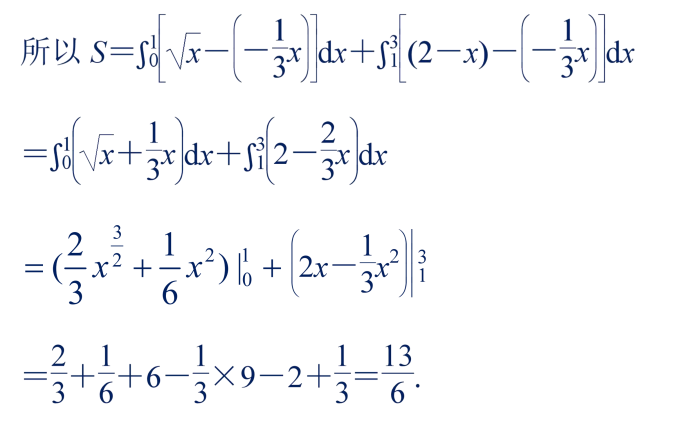
两条或两条以上的曲线围成的图形，一定要确定图形范围，通过解方程组求出交点的坐标，定出积分上、下限，若积分变量选x运算较烦琐，则积分变量可选y，同时要更换积分上、下限。

03

积分与积分基本定理的可视化解读

(本文图片与视频来自于网络，仅供学习交流用，若有侵权，请联系删除。)

人生有缘才相遇 扫码相识更有趣

微信号 :rong19711107 

公众号：周老师松果数学

● 扫码联系我

zlssgsx