前阵子,日剧“轮到你了”终于大结局了,虽然结局有点一言难尽,但黑岛和二阶堂两个学霸之间的爱情,还是很甜呢呐!两个学霸之间的默契的斐波那契数列也被许多网友认为是凶手行凶的依据。到底这数列有啥神奇之处,又该如何使用代码实现呢?一起往下看吧! 斐波那契数列,又称黄金分割数列,指的是这样一个数列:1,1,2,3,5,8,13,21,34,55…… 我们不难发现从第三项开始,每一项都等于前两项之和。以递归的方法定义就是F0=0,F1=1,Fn=Fn-1+Fn(n>=2,n∈N*)。(为了与数组下标的概念对应,F0为第0项)。通过上面的解释,相信你对斐波那契数列有一定的了解了吧,那我们来看看今天的题目吧。今天的题目就是:当你输入一个整数n后,输出斐波那契数列的第n项(从0开始,第0项为0,n<=39)。脑袋里有什么想法了么?没有的话来看看下面的三种解法吧。
斐波那契数列,又称黄金分割数列,指的是这样一个数列:1,1,2,3,5,8,13,21,34,55…… 我们不难发现从第三项开始,每一项都等于前两项之和。以递归的方法定义就是F0=0,F1=1,Fn=Fn-1+Fn(n>=2,n∈N*)。(为了与数组下标的概念对应,F0为第0项)。通过上面的解释,相信你对斐波那契数列有一定的了解了吧,那我们来看看今天的题目吧。今天的题目就是:当你输入一个整数n后,输出斐波那契数列的第n项(从0开始,第0项为0,n<=39)。脑袋里有什么想法了么?没有的话来看看下面的三种解法吧。 一、递归解法斐波那契数列具有天然的递归性,根据数学上的定义,可以得出其递推公式为:Fn=Fn-1+Fn-2(n>=2,n∈N*),基础情况为 F0=1,F1=1。对于递归解法,我们可以把问题转化为规模缩小了的同类问题的子问题,找出明确的不需要继续进行递归的条件(即基本情况base case),在本题中的基本情况为F0=0,F1=1, 当递归至基本情况后,无需继续递归,最后把子问题的解汇聚成大问题的解。
一、递归解法斐波那契数列具有天然的递归性,根据数学上的定义,可以得出其递推公式为:Fn=Fn-1+Fn-2(n>=2,n∈N*),基础情况为 F0=1,F1=1。对于递归解法,我们可以把问题转化为规模缩小了的同类问题的子问题,找出明确的不需要继续进行递归的条件(即基本情况base case),在本题中的基本情况为F0=0,F1=1, 当递归至基本情况后,无需继续递归,最后把子问题的解汇聚成大问题的解。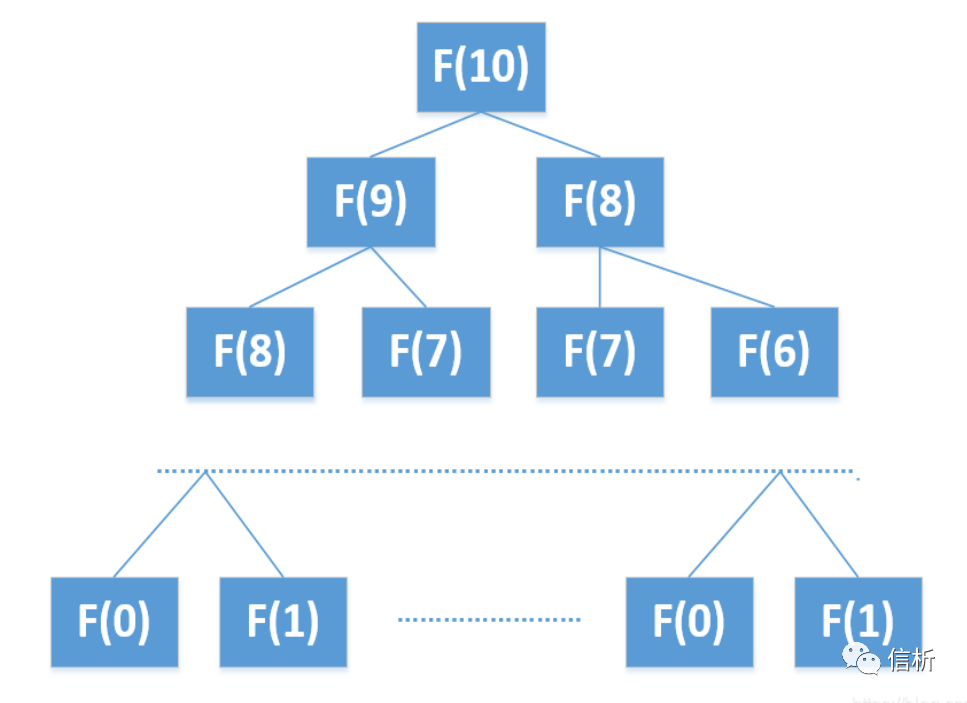 可画递归树解决递归问题
可画递归树解决递归问题 二、动态分析由于暴力递归存在大量的重复运算,降低了算法的性能。所以我们可以用动态规划方法,把运算结果存储起来,从第0项推导至第n项,避免重复运算。我们可以先思考其暴力递归的解法,把暴力递归的过程抽象成状态转移方程,确定可变参数,从基本情况(base case)开始推理,通过状态转移方程,得出最优解,从而减少冗余运算。
二、动态分析由于暴力递归存在大量的重复运算,降低了算法的性能。所以我们可以用动态规划方法,把运算结果存储起来,从第0项推导至第n项,避免重复运算。我们可以先思考其暴力递归的解法,把暴力递归的过程抽象成状态转移方程,确定可变参数,从基本情况(base case)开始推理,通过状态转移方程,得出最优解,从而减少冗余运算。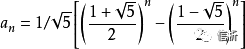
 斐波那契数列来自实现生活,有着诸多的变种问题,例如自然界中向日葵花蕊的排列线条顺时针排列线条数为21,逆时针排列线条数为34,是两个相邻的斐波那契数;树木也是以斐波那契数列的方式生长;而黄金比例也经常被用于艺术和建筑的设计,规划和建造许多建筑物,如教堂,寺庙,祭坛,住房以及创造宗教艺术品。(但其实, 斐波那契数列在“轮到你了”就真的只是个数列。)
斐波那契数列来自实现生活,有着诸多的变种问题,例如自然界中向日葵花蕊的排列线条顺时针排列线条数为21,逆时针排列线条数为34,是两个相邻的斐波那契数;树木也是以斐波那契数列的方式生长;而黄金比例也经常被用于艺术和建筑的设计,规划和建造许多建筑物,如教堂,寺庙,祭坛,住房以及创造宗教艺术品。(但其实, 斐波那契数列在“轮到你了”就真的只是个数列。) 后续我们还会持续更新一些有意思的算法基础题目,有兴趣的可以持续关注一下~ 信析团队持续招新,有兴趣了解的小可爱可以来科技楼232详谈哦(*╹▽╹*)
后续我们还会持续更新一些有意思的算法基础题目,有兴趣的可以持续关注一下~ 信析团队持续招新,有兴趣了解的小可爱可以来科技楼232详谈哦(*╹▽╹*) 祝祖国生日快乐! !
祝祖国生日快乐! !
 斐波那契数列,又称黄金分割数列,指的是这样一个数列:1,1,2,3,5,8,13,21,34,55…… 我们不难发现从第三项开始,每一项都等于前两项之和。以递归的方法定义就是F0=0,F1=1,Fn=Fn-1+Fn(n>=2,n∈N*)。(为了与数组下标的概念对应,F0为第0项)。通过上面的解释,相信你对斐波那契数列有一定的了解了吧,那我们来看看今天的题目吧。今天的题目就是:当你输入一个整数n后,输出斐波那契数列的第n项(从0开始,第0项为0,n<=39)。脑袋里有什么想法了么?没有的话来看看下面的三种解法吧。
斐波那契数列,又称黄金分割数列,指的是这样一个数列:1,1,2,3,5,8,13,21,34,55…… 我们不难发现从第三项开始,每一项都等于前两项之和。以递归的方法定义就是F0=0,F1=1,Fn=Fn-1+Fn(n>=2,n∈N*)。(为了与数组下标的概念对应,F0为第0项)。通过上面的解释,相信你对斐波那契数列有一定的了解了吧,那我们来看看今天的题目吧。今天的题目就是:当你输入一个整数n后,输出斐波那契数列的第n项(从0开始,第0项为0,n<=39)。脑袋里有什么想法了么?没有的话来看看下面的三种解法吧。 一、递归解法斐波那契数列具有天然的递归性,根据数学上的定义,可以得出其递推公式为:Fn=Fn-1+Fn-2(n>=2,n∈N*),基础情况为 F0=1,F1=1。对于递归解法,我们可以把问题转化为规模缩小了的同类问题的子问题,找出明确的不需要继续进行递归的条件(即基本情况base case),在本题中的基本情况为F0=0,F1=1, 当递归至基本情况后,无需继续递归,最后把子问题的解汇聚成大问题的解。
一、递归解法斐波那契数列具有天然的递归性,根据数学上的定义,可以得出其递推公式为:Fn=Fn-1+Fn-2(n>=2,n∈N*),基础情况为 F0=1,F1=1。对于递归解法,我们可以把问题转化为规模缩小了的同类问题的子问题,找出明确的不需要继续进行递归的条件(即基本情况base case),在本题中的基本情况为F0=0,F1=1, 当递归至基本情况后,无需继续递归,最后把子问题的解汇聚成大问题的解。 可画递归树解决递归问题
可画递归树解决递归问题public class Solution { public int Fibonacci(int n) { //base case if (n==0){ return 0; } if(n==1){ return 1; } return Fibonacci(n-1)+Fibonacci(n-2); }}①子问题个数,即递归树中节点的总数,而二叉树节点总数为指数级别,所以子问题个数为 O(2^n);而解决一个子问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2)f(n−1)+f(n−2) 一个加法操作,所以时间为O(1)。故我们可以得到这个算法的时间复杂度为 O(2^n),指数级别。
②而在递归过程中,需要在存储递归过程中的运算结果,最大空间为树的高度h(即n),而时间复杂度:O(2^n),故空间复杂度:O(h) 即O(n)。问题分析:观察递归树,很明显发现了算法低效的原因:存在大量重复计算,运算的规模与n的大小成指数关系,因此这个暴力递归算法虽然简洁明了,但运行效率低下。 二、动态分析由于暴力递归存在大量的重复运算,降低了算法的性能。所以我们可以用动态规划方法,把运算结果存储起来,从第0项推导至第n项,避免重复运算。我们可以先思考其暴力递归的解法,把暴力递归的过程抽象成状态转移方程,确定可变参数,从基本情况(base case)开始推理,通过状态转移方程,得出最优解,从而减少冗余运算。
二、动态分析由于暴力递归存在大量的重复运算,降低了算法的性能。所以我们可以用动态规划方法,把运算结果存储起来,从第0项推导至第n项,避免重复运算。我们可以先思考其暴力递归的解法,把暴力递归的过程抽象成状态转移方程,确定可变参数,从基本情况(base case)开始推理,通过状态转移方程,得出最优解,从而减少冗余运算。public class Solution { public int Fibonacci(int n) { //基本情况 if (n==0){ return 0; } if (n<=1){ return 1; } int dp[]=new int[n+1]; dp[0]=0; dp[1]=1; for(int i=2;i //状态转移方程 dp[i]=dp[i-1]+dp[i-2]; } return dp[n]; }}细心的你会发现,根据斐波那契数列的状态转移方程,当前状态只和之前的两个状态有关,其实并不需要那么长的一个 DP 数组来存储所有的状态,只要想办法存储之前的两个状态就行了。所以可以进一步优化,把空间复杂度降为 O(1)。
三、斐波那契数列通项公式 对于这道题目,我们还可以通过斐波那契数列通项公式求解,但这个数学方法仅限于标准的斐波那契数列问题求解,无法应对斐波那契数列的变种问题。公式如下: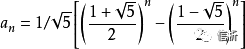
public class Solution { public int Fibonacci(int n) { Long fib = Math.round((Math.pow((1 + Math.sqrt(5)) / 2, n) - Math.pow((1 - Math.sqrt(5)) / 2, n)) / Math.sqrt(5)); return fib.intValue(); }} 斐波那契数列来自实现生活,有着诸多的变种问题,例如自然界中向日葵花蕊的排列线条顺时针排列线条数为21,逆时针排列线条数为34,是两个相邻的斐波那契数;树木也是以斐波那契数列的方式生长;而黄金比例也经常被用于艺术和建筑的设计,规划和建造许多建筑物,如教堂,寺庙,祭坛,住房以及创造宗教艺术品。(但其实, 斐波那契数列在“轮到你了”就真的只是个数列。)
斐波那契数列来自实现生活,有着诸多的变种问题,例如自然界中向日葵花蕊的排列线条顺时针排列线条数为21,逆时针排列线条数为34,是两个相邻的斐波那契数;树木也是以斐波那契数列的方式生长;而黄金比例也经常被用于艺术和建筑的设计,规划和建造许多建筑物,如教堂,寺庙,祭坛,住房以及创造宗教艺术品。(但其实, 斐波那契数列在“轮到你了”就真的只是个数列。)更多精彩内容:
(点击即可阅读)
用两个栈实现队列用队列实现栈持续更新中..... 后续我们还会持续更新一些有意思的算法基础题目,有兴趣的可以持续关注一下~ 信析团队持续招新,有兴趣了解的小可爱可以来科技楼232详谈哦(*╹▽╹*)
后续我们还会持续更新一些有意思的算法基础题目,有兴趣的可以持续关注一下~ 信析团队持续招新,有兴趣了解的小可爱可以来科技楼232详谈哦(*╹▽╹*) 祝祖国生日快乐! !
祝祖国生日快乐! !
--点赞与评论树)
)


)

)





)

![【共读Primer】55.[6.4]函数重载--重载与作用域 Page210](http://pic.xiahunao.cn/【共读Primer】55.[6.4]函数重载--重载与作用域 Page210)
用法及代码示例)
 —— 程序的签名打包并在手机上运行)

