
1 引言
在工程实践中,一个工程项目往往由若干个子项目组成。这些子项目间往往有两种关系:
(1) 先后关系,即必须在某个项完成后才能开始实施另一个子项目。
(2) 子项目间无关系,即两个子项目可以同时进行,互不影响。
例如:在工厂里产品的生产线上,一个产品由若干个零部件组成。零部件生产时,也存在这两种关系:
(1)先后关系,即一个部件必须在完成后才能生产另一个部件;
(2)部件间无先后关系,即这两个部件可以同时生产。
那么如何合理的分配资源才能保证工程能够按时完成呢?将任务作为图的顶点,将任务之间的依赖关系作为图的边,这样就可以将实际问题抽象为数据结构图论中的典型问题——图的拓扑排序。
2 重要概念
有向无环图(Directed Acyclic Graph, DAG)是有向图的一种,字面意思的理解就是图中没有环。常常被用来表示事件之间的驱动依赖关系,管理任务之间的调度。AOV网:在每一个工程中,可以将工程分为若干个子工程,这些子工程称为活动。如果用图中的顶点表示活动,以有向图的弧表示活动之间的优先关系,这样的有向图称为AOV网,即顶点表示活动的网。在AOV网中,如果从顶点vi到顶点j之间存在一条路径,则顶点vi是顶点vj的前驱,顶点vj是顶点vi的后继。活动中的制约关系可以通过AOV网中的表示。 在AOV网中,不允许出现环,如果出现环就表示某个活动是自己的先决条件。因此需要对AOV网判断是否存在环,可以利用有向图的拓扑排序进行判断。拓扑序列:设G=(V,E)是一个具有n个顶点的有向图,V中的顶点序列v1,v2,…,vn,满足若从顶点vi到vj有一条路径,则在顶点序列中顶点vi必在vj之前,则我们称这样的顶点序列为一个拓扑序列。拓扑排序:拓扑排序是对一个有向图构造拓扑序列的过程。
3 拓扑排序
拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
(1)每个顶点出现且只出现一次。
(2)若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
注:有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
4 入度表法
入度表法是根据顶点的入度来判断是否存在依赖关系。若顶点入度不为0。则必然此顶点的事件有前驱依赖事件,因此每次选取入度为0的顶点输出,则符合拓扑排序的性质。
4.1 算法流程
(1)从图中选择一个入度为0的顶点,输出该顶点。
(2)从图中删除该节点及其所有出边(即与之邻接的所有顶点入度-1)
(3)反复执行这两个步骤,直至所有节点都输出,即整个拓扑排序完成;或者直至剩下的图中再没有入度为0的节点,这就说明此图中有回路,不可能进行拓扑排序。
4.2 实例图解
例如:图4.2.1所示的有向无环图,采用入度表的方法获取拓扑排序过程。
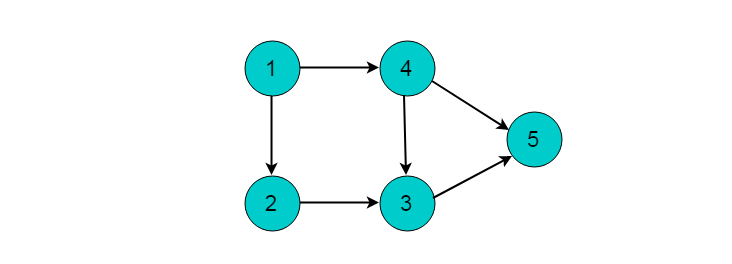
(1)选择图中入度为0的顶点1,输出顶点1。删除顶点1,并删除以顶点1为尾的边。删除后图为:
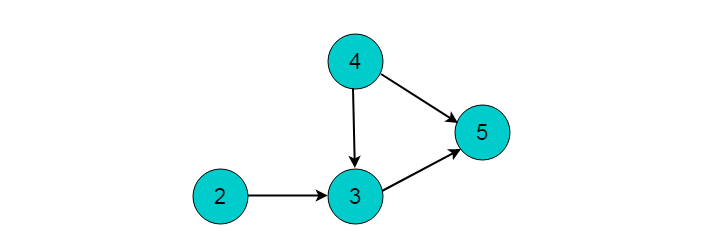
(2)继续选择入度为0的顶点。现在,图中入度为0的顶点有2和4,这里我们选择顶点2,输出顶点2。删除顶点2,并删除以顶点2为尾的边。删除后图为:
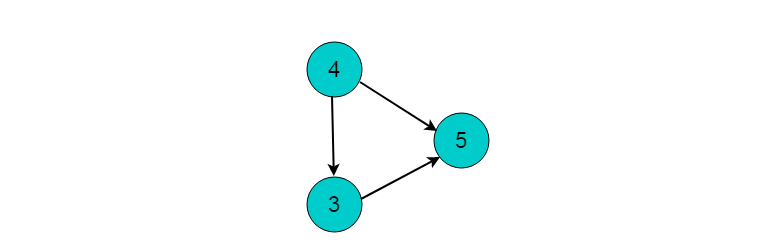
(3)选择入度为0的顶点4,输出顶点4.删除顶点4,并删除以顶点4为尾的边。删除后图为:
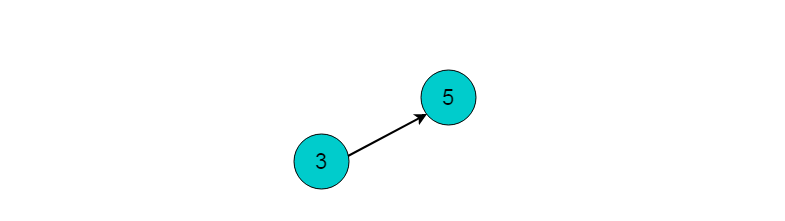
(4)选择入度为0的顶点3,输出顶点3.删除顶点3,并删除以顶点3为尾的边。删除后图为:

(5)最后剩余顶点5,输出顶点5,拓扑排序过程结束。最终的输出结果为:
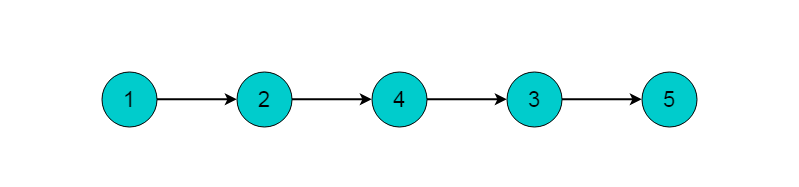
4.3 性能分析
算法时间复杂度分析:统计所有节点入度的时间复杂性为(VE);接下来删边花费的时间也是(VE),总花费时间为O(VE)。若使用队列保存入度为0的顶点,则可以将这个算法复杂度将为O(V+E)。
5 DFS方法
深度优先搜索过程中,当到达出度为0的顶点时,需要进行回退。在执行回退时记录出度为0的顶点,将其入栈。则最终出栈顺序的逆序即为拓扑排序序列。
5.1 算法流程
(1)对图执行深度优先搜索。
(2)在执行深度优先搜索时,若某个顶点不能继续前进,即顶点的出度为0,则将此顶点入栈。
(3)最后得到栈中顺序的逆序即为拓扑排序顺序。
5.2 实例图解
例如图5.2.1所示的有向无环图,采用DFS的方法获取拓扑排序过程。
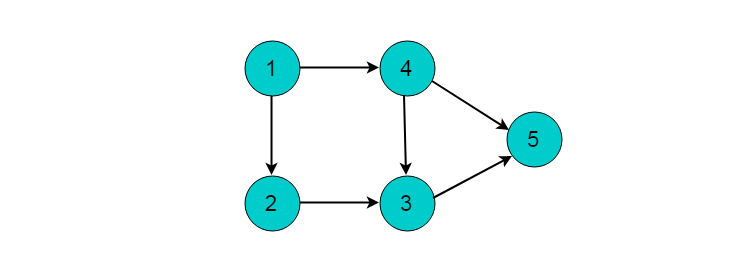
(1)选择起点为顶点1,,开始执行深度优先搜索。顺序为1->2->3->5。
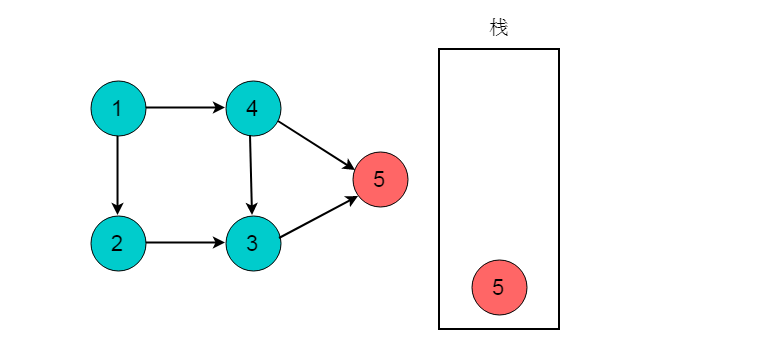
(2)深度优先搜索到达顶点5时,顶点5出度为0。将顶点5入栈。
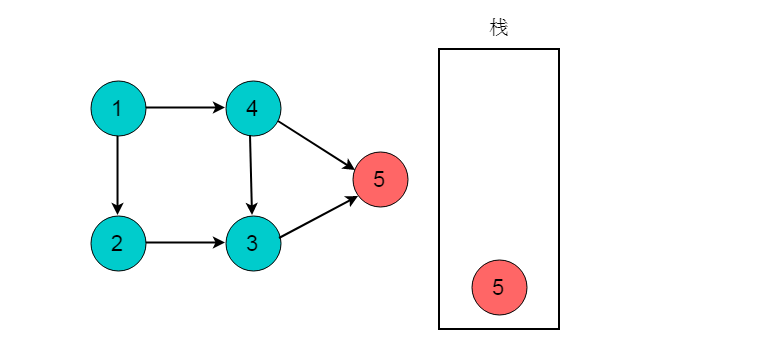
(3)深度优先搜索执行回退,回退至顶点3。此时顶点3的出度为0,将顶点3入栈。
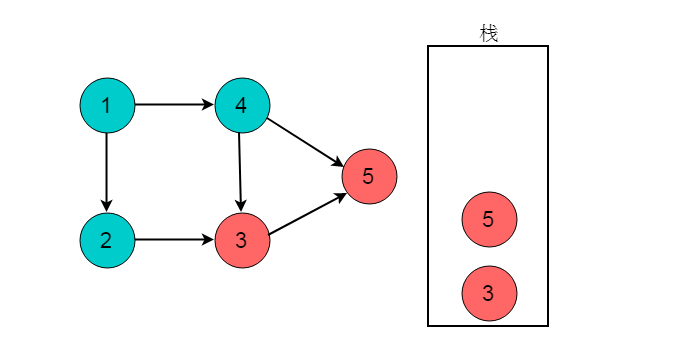
(4)回退至顶点2,顶点2出度为0,顶点2入栈。
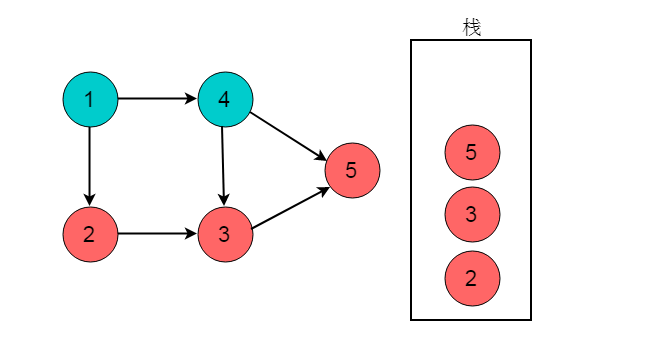
(5)回退至顶点1,顶点1可以前进位置为顶点4,顺序为1->4。

(6)顶点4出度为0,顶点4入栈。
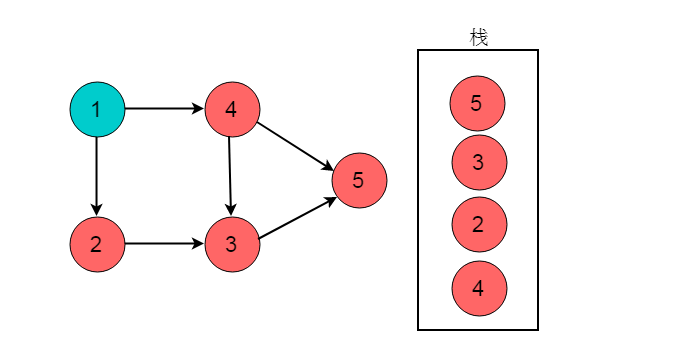
(7)回退至顶点1,顶点1出度为0,顶点1入栈。
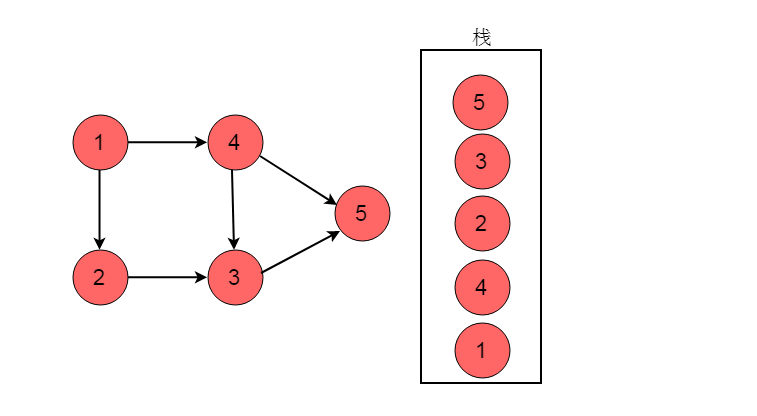
(8)栈的逆序为1->4->2->3->5。此顺序为拓扑排序结果。
5.3 性能分析
时间复杂度分析:首先深度优先搜索的时间复杂度为O(V+E),而每次只需将完成访问的顶点存入数组中,需要O(1),因而总复杂度为O(V+E)。
推荐阅读
拜托,面试官别问我「布隆」了
有点难度,几道和「滑动窗口」有关的算法面试题
数据结构与算法:三十张图弄懂「图的两种遍历方式」
昨天,终于拿到了腾讯 offer
几道和「二叉树」有关的算法面试题
几道和散列(哈希)表有关的面试题
一道看完答案你会觉得很沙雕的「动态规划算法题」
几道和「堆栈、队列」有关的面试算法题
链表算法面试问题?看我就够了!
我就知道你在看!)

)
无法打开qtcreator)






)

 —— HTML语言的语法解析)
)


)


