Solution
和后面两道题难度差距太大了吧！！
显然就只是个小模拟，注意判0就行了。
Code
#include<bits/stdc++.h> using namespace std;char s[100005];int main() {freopen("expression.in", "r", stdin);freopen("expression.out", "w", stdout);scanf("%s", s);int flag = 0, len = strlen(s);for(int i = 0; i < len; i ++) {int t = s[i];if(t >= '0' && t <= '9') {if(flag) {printf("%c", t);flag = 0;if(s[i + 1] != '-' && s[i + 1] != '+' && i + 1 < len) {if(s[i + 1] != '0') printf("+");else {while(s[i + 1] == '0') {printf("+0"); i ++;}if(s[i + 1] >= '0' && s[i + 1] <= '9')printf("+");}}} else {printf("%c", t);}} else {if(t == '-') flag = 1;printf("%c", t);}}return 0; }
Solution
思维难度很大啊，需要把所有的情况理清楚，代码就不难写了。
性质1：如果有超过1条特殊边与树边形成奇环，则满足条件的边不可能是特殊边（肯定不可能被所有奇环包含）
性质2：如果一条特殊边与另一条特殊边形成环，这种环没有任何用处
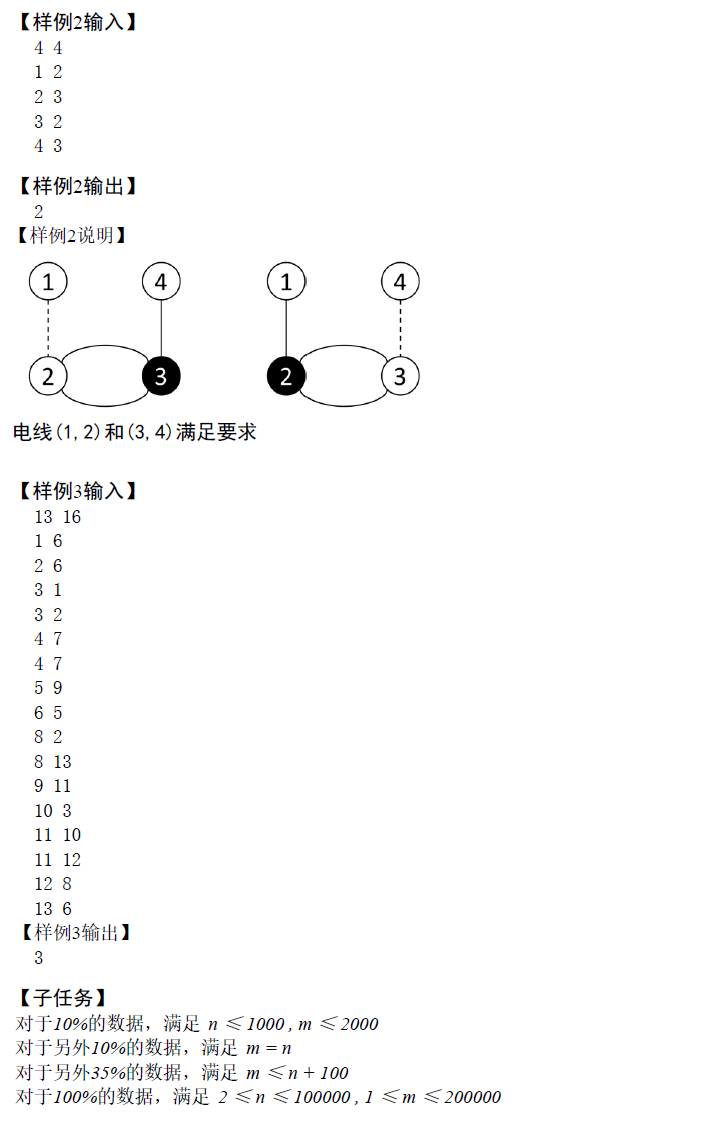
情况1：两个与树边形成奇环的边 一定产生一个偶环(2,3,4,5) 但偶环上的边不可能被所有奇环
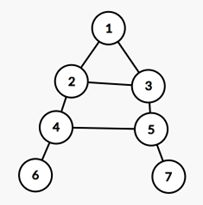
情况2：两个偶环 本来他们的边就全部不满足条件 不用考虑多生成的新偶环(2,4,7,5)
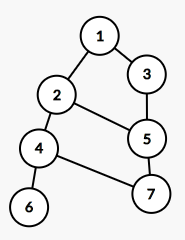
情况3：一个奇环+一个偶环 生成一个奇环(2,5,7,6,4) 这个奇环的树边本来就在原奇环上 无需考虑
建一棵DFS树，则特殊边就全部为返祖边 用odd [u]对结点u统计奇环,even[u]统计偶环 设一条返祖边为 u-> v 若它形成奇环，则odd[u]++,odd[v]--. 则u的子树所有结点的odd之和，即为u -> fa这条边被多少奇环包含 （差分前缀和的思想）（树上差分）
唯一非树边会有贡献的情况就是有且仅有一个奇环，此时一定只有一条非树边在奇环内 提供贡献
Code
#include<bits/stdc++.h> #define RG register using namespace std;int n, m; struct Node {int u, v, nex;Node(int u = 0, int v = 0, int nex = 0) :u(u), v(v), nex(nex) { } } Edge[400005];int h[100005], stot = 1; void add(int u, int v) {Edge[++stot] = Node(u, v, h[u]);h[u] = stot; }int fae[100005], vis[100005], vise[400005], odd[100005], even[100005], cnto, cnte, dep[100005]; void dfs(int u) {vis[u] = 1;for(int i = h[u]; i; i = Edge[i].nex) {int v = Edge[i].v;if(vise[i]) continue;vise[i] = vise[i ^ 1] = 1;if(vis[v]) {if((dep[v] & 1) == (dep[u] & 1)) {odd[u] ++;odd[v] --;cnto ++;} else {even[u] ++;even[v] --;cnte ++;}} else {fae[v] = i;dep[v] = dep[u] + 1;dfs(v);}} }void dfs2(int u) {for(int i = h[u]; i; i = Edge[i].nex) {int v = Edge[i].v;if(fae[v] == i) {dfs2(v);odd[u] += odd[v];even[u] += even[v];}} }int main() {freopen("voltage.in", "r", stdin);freopen("voltage.out", "w", stdout);scanf("%d%d", &n, &m);for(int i = 1; i <= m; i ++) {int u, v;scanf("%d%d", &u, &v);add(u, v); add(v, u);}dfs(1); dfs2(1);int ans = 0;for(int i = 1; i <= n; i ++)if(fae[i] != 0 && odd[i] == cnto && !even[i])ans ++;if(cnto == 1) ans ++;printf("%d\n", ans);return 0; }
