小a与黄金街道(欧拉函数)/**模运算规则总结*/

 

链接：https://ac.nowcoder.com/acm/contest/317/D
来源：牛客网

• 题目描述
  小a和小b来到了一条布满了黄金的街道上。它们想要带几块黄金回去，然而这里的城管担心他们拿走的太多，于是要求小a和小b通过做一个游戏来决定最后得到的黄金的数量。
  游戏规则是这样的：假设道路长度为n米(左端点为0，右端点为n)，同时给出一个数k(下面会提到k的用法)设小a初始时的黄金数量为A，小b初始时的黄金数量为B小a从1出发走向n−1，小b从n−1出发走向1，两人的速度均为1m/s
  假设某一时刻(必须为整数)小a的位置为x,小b的位置为y,若gcd(n,x)=1且gcd(n,y)=1，那么小a的黄金数量会变为A∗k^x(kg),小b的黄金数量,B会变为B∗k^y(kg)当小a到达n−1时游戏结束,小a想知道在游戏结束时A+B的值,答案对10⁹+7取模
• 输入描述:
  一行四个整数n,k,A,B
• 输出描述:
  输出一个整数表示答案
• 示例1
  输入
  4 2 1 1
  输出
  32
• 示例2
  输入
  5 1 1 1
  输出
  2
• 备注:3⩽n⩽10⁸,1⩽A,B,k⩽10¹³

示例1说明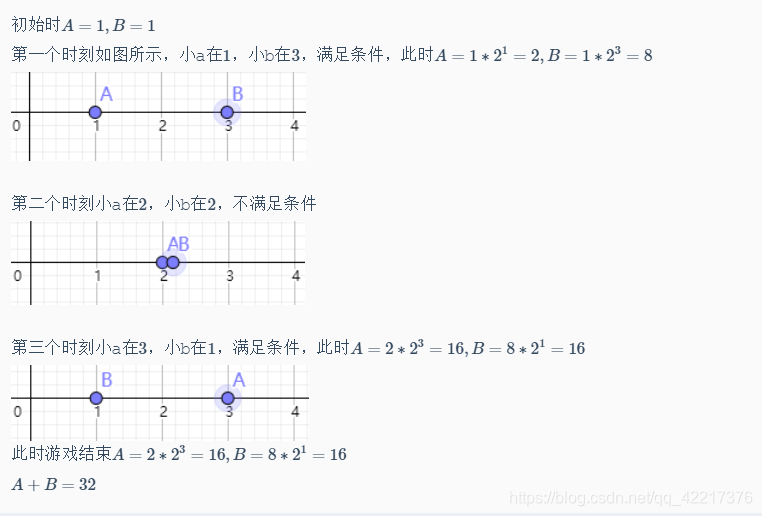

官方题解

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector> 
#define pi 3.1415926
#define mod 1000000007
using namespace std;//typedef pair<int,int> Node;
typedef long long  LL;
const int Max_n=10005;
int prime[Max_n],is_prime[Max_n];
int j;void GetPrime(){for(int i=2;i<=Max_n;i++) is_prime[i]=1;for(int i=2;i<=sqrt(Max_n);i++){if(is_prime[i]){for(int j=i*i;j<=Max_n;j+=i)is_prime[j]=0;}}j=1;for(int i=2;i<=Max_n;i++)if(is_prime[i])prime[j++]=i;
}
//欧拉函数
LL phi(LL n){LL ans=1;for(int i=1;i<j;i++){if(n%prime[i]==0){//存在素因子int num=0;//当前素因子的个数while(n%prime[i]==0){num++;n/=prime[i];}for(int k=1;k<num;k++) ans=(ans*prime[i])%mod;ans=(ans*(prime[i]-1))%mod;//此处和上面注意这里是prime[i]if(n==1) break;}}if(n>1) ans=n-1;//n是素数return ans;
}LL Qpow(LL a,LL b){LL ans=1;LL res=a%mod;while(b){if(b&1) ans=(ans*res)%mod;res=(res*res)%mod;b>>=1;}return ans;
}
int main(){GetPrime();//这里不要忘记LL n,k,a,b;scanf("%lld%lld%lld%lld",&n,&k,&a,&b);LL ans=((a+b)%mod*Qpow(k,n*phi(n)/2));//模运算规则((a^b)%p)=((a%p)^b)%p printf("%lld",ans%mod);return 0;
}

• 模运算规则
  (a±b)%p=(a%p±b%p)%p
  (a * b)%p=(a%p * b%p)%p
  a^b%p=(a%p)^b%p