树


树的表示方式有
- 树形图表示法:逻辑结构描述直观
- 嵌套集合表示法(文氏图表示法)
- 凹入表示法
- 广义表表示法
二叉树
二叉树是另一种重要的树形结构,是度为2的有序树,它的特点是每个结点至多有两棵子树。
二叉树的递归定义
二叉树是n(n≥0)个结点的有限集。它或者是空集(n=0),或者同时满足以下两个条件:
(1) 有且仅有一个根结点;
(2) 其余的结点分成两棵互不相交的左子树和右子树。
二叉树的特点
如果二叉树的根结点只有一棵子树,必须明确区分它是左子树还是右子树,因为两者将构成不同形态的二叉树。
注意:二叉树不是树的特例。它们是两种不同的数据结构。
二叉树举例
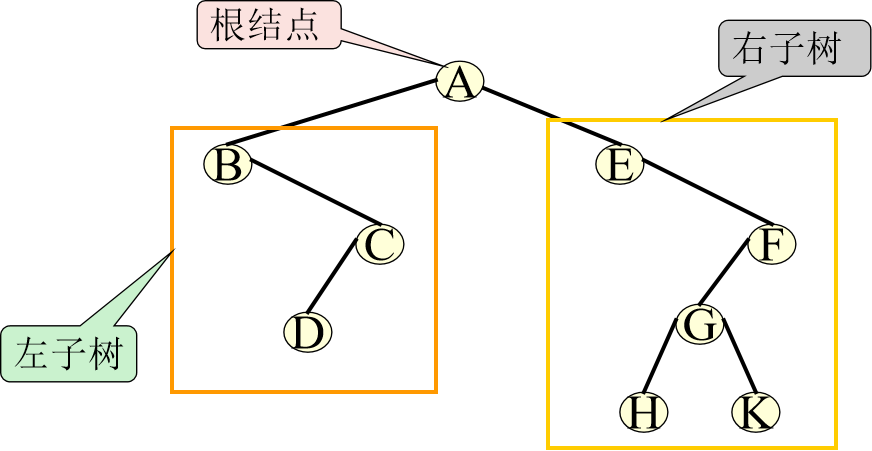
二叉树的性质
性质1:在二叉树的第i层上至多有2i-1 个结点。 (i≥1)

性质2:深度为 k 的二叉树上至多含 2k-1 个结点(k≥1)
证明:

性质3:对任何一棵二叉树,若它含有n0个叶子结点、n2个度为2的结点,则必存在关系式:n0= n2+1。
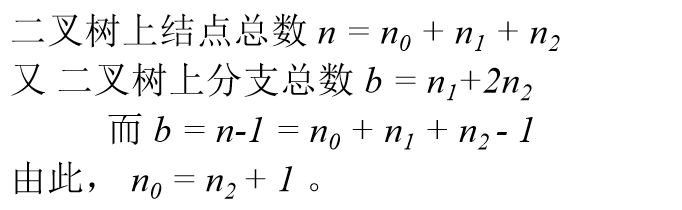
即 叶子结点数=度2结点 + 1
性质4:具有n个结点的完全二叉树的深度为 [log2n] +1 下取整
证明:

性质5:
若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号,则对完全二叉树中任意一个编号为 i 的结点:
(1) 若 i=1,则该结点是二叉树的根,无双亲, 否则,编号为 i/2 的结点为其双亲结点;
(2) 若 2i>n,则该结点无左孩子,否则,编号为 2i 的结点为其左孩子结点;
(3) 若 2i+1>n,则该结点无右孩子结点, 否则,编号为2i+1 的结点为其右孩子结点。
两类特殊的二叉树:
满二叉树
指的是深度为k且含有2k - 1个结点的二叉树。
特点:
(1)每一层上结点数都达到最大
(2)度为1的结点n1=0,树叶都在最下一层。
满二叉树结点层序编号方法:
从根结点起从上到下逐层(层内从左到右)对二叉树的结点进行连续编号。
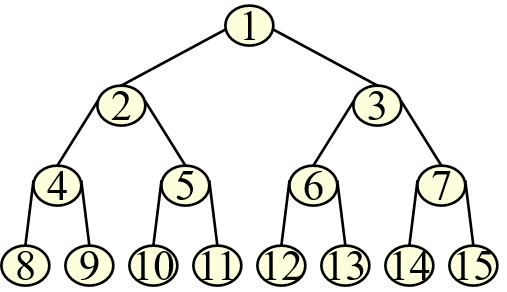
完全二叉树
树中所含的 n 个结点和满二叉树中编号为 1 至 n 的结点一一对应。
完全二叉树的特点:
1、满二叉树是完全二叉树,完全二叉树不一定是满二叉树;
2、在完全二叉树中,若某个结点没有左孩子,则它一定没有右孩子,即该结点必是叶结点。
二叉树的存储结构:
1.顺序存储结构
用一组地址连续的存储单元,以层序顺序存放二叉树的数据元素,结点的相对位置蕴含着结点之间的关系。
如完全二叉树
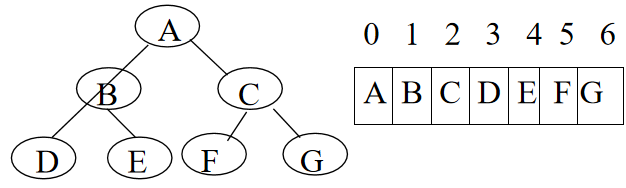
非完全二叉树,存储时必须将相应的位置空出来,使存放的结果符合完全二叉树的形状。
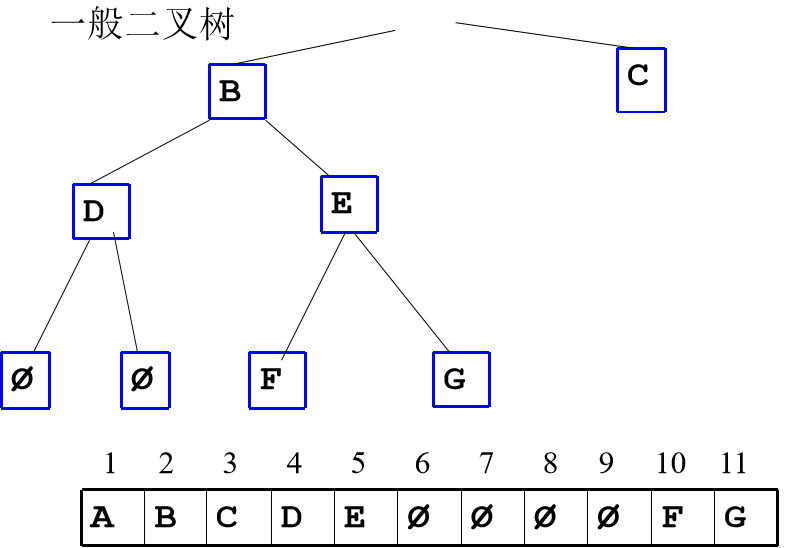
所以,二叉树顺序存储结构仅适用于完全二叉树。
若存储非完全二叉树时有可能对存储空间造成极大的浪费:
在最坏的情况下,一个深度为K且只有K个结点的右单支树需要2K-1个结点存储空间。
二叉树的链式存储结构
根据二叉树的非线性结构的特点,常用链式存储方式来表示二叉树。
二叉树的链式存储结构有3种,它们是二叉链表、三叉链表和线索链表。
二叉链表存储结构
把每个结点分成三个域:一个域存放结点本身的信息,另外两个是指针域,分别存放左、右孩子的地址。每个结点的结构表示为:
![]()
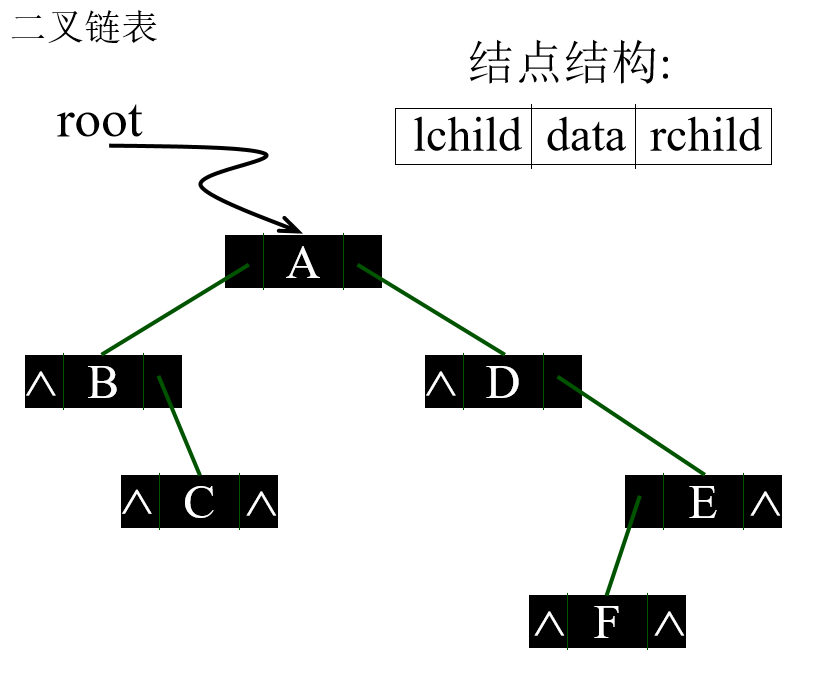
二叉链表的C 语言类型描述如下:
typedef char TElemType; typedef struct Node { TElemType data;struct Node *lchild, *rchild; } BiTNode, *BiTree;

三叉链表(带双亲指针的二叉链表)
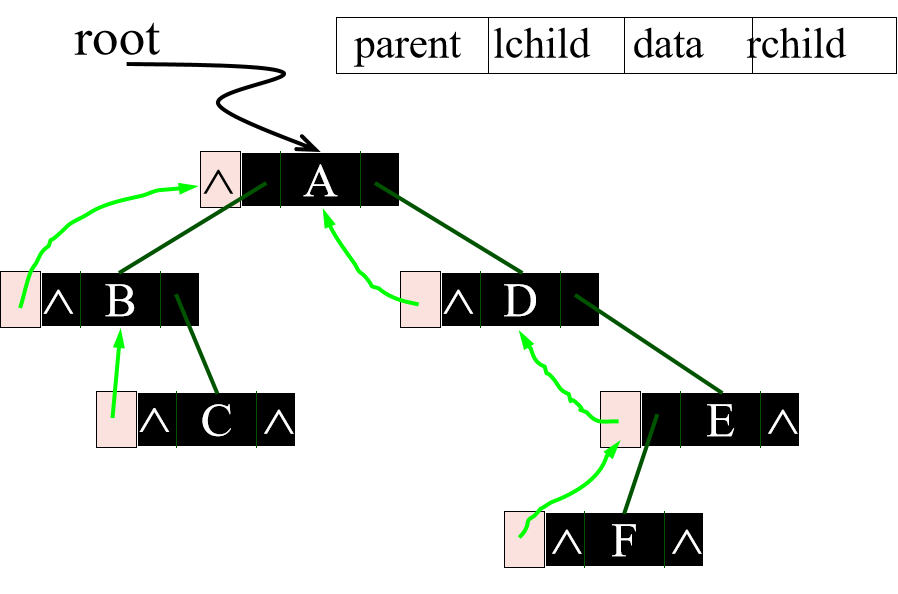





)



)




)


数组填充的实现)
)
