程序员编程艺术:第二章、字符串是否包含及相关问题扩展
作者:July,yansha。
时间:二零一一年四月二十三日。
致谢:老梦,nossiac,Hession,Oliver,luuillu,雨翔,啊菜,及微软100题实现小组所有成员。
微博:http://weibo.com/julyweibo。
出处:http://blog.csdn.net/v_JULY_v。
-------------------------------------------
目录
曲之前奏
第一节、一道俩个字符串是否包含的问题
1.1、O(n*m)的轮询方法
1.2、O(mlogm)+O(nlogn)+O(m+n)的排序方法
1.3、O(n+m)的计数排序方法
第二节
2.1、O(n+m)的hashtable的方法
2.2、O(n+m)的数组存储方法
第三节、O(n)到O(n+m)的素数方法
第四节、字符串是否包含问题的继续补充
4.1、Bit-map
4.2、移位操作
第五节、字符串相关问题扩展
5.1、字符串匹配问题
5.2、在字符串中查找子串
扩展:在一个字符串中找到第一个只出现一次的字符
5.3、字符串转换为整数
5.4、字符串拷贝
前奏
前一章,请见这:程序员面试题狂想曲:第一章、左旋转字符串。本章里出现的所有代码及所有思路的实现,在此之前,整个网上都是没有的。
文中的思路,聪明点点的都能想到,巧的思路,大师也已奉献了。如果你有更好的思路,欢迎提供。如果你对此狂想曲系列有任何建议,欢迎微博上交流或来信指导。任何人,有任何问题,欢迎随时不吝指正。
如果此狂想曲系列对你有所帮助,我会非常之高兴,并将让我有了永久坚持写下去的动力。谢谢。
第一节、一道俩个字符串是否包含的问题
1.0、题目描述:
假设这有一个各种字母组成的字符串,假设这还有另外一个字符串,而且这个字符串里的字母数相对少一些。从算法是讲,什么方法能最快的查出所有小字符串里的字母在大字符串里都有?
比如,如果是下面两个字符串:
String 1: ABCDEFGHLMNOPQRS
String 2: DCGSRQPOM
答案是true,所有在string2里的字母string1也都有。
如果是下面两个字符串:
String 1: ABCDEFGHLMNOPQRS
String 2: DCGSRQPOZ
答案是false,因为第二个字符串里的Z字母不在第一个字符串里。
点评:
1、题目描述虽长,但题意简单明了,就是给定一长一短的俩个字符串A,B,假设A长B短,现在,要你判断B是否包含在字符串A中,即B?(-A。
2、题意虽简单,但实现起来并不轻松,且当如果面试官步步紧逼,一个一个否决你能想到的方法,要你给出更好、最好的方案时,你恐怕就要伤不少脑筋了。
ok,在继续往下阅读之前,您最好先想个几分钟,看你能想到的最好方案是什么,是否与本文最后实现的方法一致。
1.1、O(n*m)的轮询方法
判断string2中的字符是否在string1中?:
String 1: ABCDEFGHLMNOPQRS
String 2: DCGSRQPOM
判断一个字符串是否在另一个字符串中,最直观也是最简单的思路是,针对第二个字符串string2中每一个字符,一一与第一个字符串string1中每个字符依次轮询比较,看它是否在第一个字符串string1中。
假设n是字符串string1的长度,m是字符串string2的长度,那么此算法,需要O(n*m)次操作,拿上面的例子来说,最坏的情况下将会有16*8 = 128次操作。
我们不难写出以下代码:
#include <iostream> using namespace std; int compare(string str1,string str2) { for (int i=0; i<str2.length(); i++) { for (int j=0; j<str1.length(); j++) //O(n*m) { if (str2[i] == str1[j]) //一一比较 { break; } } if (j==str1.length()) { cout << "false" << endl; return 0; } } cout << "true" << endl; return 1; } int main() { string str1="ABCDEFGHLMNOPQRS"; string str2="DCGSRQPOM"; compare(str1,str2); return 0; }
上述代码的时间复杂度为O(n*m),显然,时间开销太大,我们需要找到一种更好的办法。
1.2、O(mlogm)+O(nlogn)+O(m+n)的排序方法
一个稍微好一点的方案是先对这两个字符串的字母进行排序,然后同时对两个字串依次轮询。两个字串的排序需要(常规情况)O(m log m) + O(n log n)次操作,之后的线性扫描需要O(m+n)次操作。
同样拿上面的字串做例子,将会需要16*4 + 8*3 = 88加上对两个字串线性扫描的16 + 8 = 24的操作。(随着字串长度的增长,你会发现这个算法的效果会越来越好)
关于采用何种排序方法,我们采用最常用的快速排序,下面的快速排序的代码用的是以前写的,比较好懂,并且,我执意不用库函数的qsort代码。唯一的问题是,此前写的代码是针对整数进行排序的,不过,难不倒我们,稍微改一下参数,即可,如下:
//copyright@ 2011 July && yansha //July,updated,2011.04.23. #include <iostream> #include <string> using namespace std; //以前的注释,还让它保留着 int partition(string &str,int lo,int hi) { int key = str[hi]; //以最后一个元素,data[hi]为主元 int i = lo - 1; for(int j = lo; j < hi; j++) ///注,j从p指向的是r-1,不是r。 { if(str[j] <= key) { i++; swap(str[i], str[j]); } } swap(str[i+1], str[hi]); //不能改为swap(&data[i+1],&key) return i + 1; } //递归调用上述partition过程,完成排序。 void quicksort(string &str, int lo, int hi) { if (lo < hi) { int k = partition(str, lo, hi); quicksort(str, lo, k - 1); quicksort(str, k + 1, hi); } } //比较,上述排序O(m log m) + O(n log n),加上下面的O(m+n), //时间复杂度总计为:O(mlogm)+O(nlogn)+O(m+n)。 void compare(string str1,string str2) { int posOne = 0; int posTwo = 0; while (posTwo < str2.length() && posOne < str1.length()) { while (str1[posOne] < str2[posTwo] && posOne < str1.length() - 1) posOne++; //如果和str2相等,那就不能动。只有比str2小,才能动。 if (str1[posOne] != str2[posTwo]) break; //posOne++; //归并的时候,str1[str1Pos] == str[str2Pos]的时候,只能str2Pos++,str1Pos不可以自增。 //多谢helloword指正。 posTwo++; } if (posTwo == str2.length()) cout << "true" << endl; else cout << "false" << endl; } int main() { string str1 = "ABCDEFGHLMNOPQRS"; string str2 = "DCGDSRQPOM"; //之前上面加了那句posOne++之所以有bug,是因为,@helloword: //因为str1如果也只有一个D,一旦posOne++,就到了下一个不是'D'的字符上去了, //而str2有俩D,posTwo++后,下一个字符还是'D',就不等了,出现误判。 quicksort(str1, 0, str1.length() - 1); quicksort(str2, 0, str2.length() - 1); //先排序 compare(str1, str2); //后线性扫描 return 0; }
1.3、O(n+m)的计数排序方法
此方案与上述思路相比,就是在排序的时候采用线性时间的计数排序方法,排序O(n+m),线性扫描O(n+m),总计时间复杂度为:O(n+m)+O(n+m)=O(n+m)。
代码如下:
#include <iostream> #include <string> using namespace std; // 计数排序,O(n+m) void CounterSort(string str, string &help_str) { // 辅助计数数组 int help[26] = {0}; // help[index]存放了等于index + 'A'的元素个数 for (int i = 0; i < str.length(); i++) { int index = str[i] - 'A'; help[index]++; } // 求出每个元素对应的最终位置 for (int j = 1; j < 26; j++) help[j] += help[j-1]; // 把每个元素放到其对应的最终位置 for (int k = str.length() - 1; k >= 0; k--) { int index = str[k] - 'A'; int pos = help[index] - 1; help_str[pos] = str[k]; help[index]--; } } //线性扫描O(n+m) void Compare(string long_str,string short_str) { int pos_long = 0; int pos_short = 0; while (pos_short < short_str.length() && pos_long < long_str.length()) { // 如果pos_long递增直到long_str[pos_long] >= short_str[pos_short] while (long_str[pos_long] < short_str[pos_short] && pos_long < long_str.length () - 1) pos_long++; // 如果short_str有连续重复的字符,pos_short递增 while (short_str[pos_short] == short_str[pos_short+1]) pos_short++; if (long_str[pos_long] != short_str[pos_short]) break; pos_long++; pos_short++; } if (pos_short == short_str.length()) cout << "true" << endl; else cout << "false" << endl; } int main() { string strOne = "ABCDAK"; string strTwo = "A"; string long_str = strOne; string short_str = strTwo; // 对字符串进行计数排序 CounterSort(strOne, long_str); CounterSort(strTwo, short_str); // 比较排序好的字符串 Compare(long_str, short_str); return 0; }
不过上述方法,空间复杂度为O(n+m),即消耗了一定的空间。有没有在线性时间,且空间复杂度较小的方案列?
第二节、寻求线性时间的解法
2.1、O(n+m)的hashtable的方法
上述方案中,较好的方法是先对字符串进行排序,然后再线性扫描,总的时间复杂度已经优化到了:O(m+n),貌似到了极限,还有没有更好的办法列?
我们可以对短字串进行轮询(此思路的叙述可能与网上的一些叙述有出入,因为我们最好是应该把短的先存储,那样,会降低题目的时间复杂度),把其中的每个字母都放入一个Hashtable里(我们始终设m为短字符串的长度,那么此项操作成本是O(m)或8次操作)。然后轮询长字符串,在Hashtable里查询短字符串的每个字符,看能否找到。如果找不到,说明没有匹配成功,轮询长字符串将消耗掉16次操作,这样两项操作加起来一共只有8+16=24次。
当然,理想情况是如果长字串的前缀就为短字串,只需消耗8次操作,这样总共只需8+8=16次。
或如梦想天窗所说: 我之前用散列表做过一次,算法如下:
1、hash[26],先全部清零,然后扫描短的字符串,若有相应的置1,
2、计算hash[26]中1的个数,记为m
3、扫描长字符串的每个字符a;若原来hash[a] == 1 ,则修改hash[a] = 0,并将m减1;若hash[a] == 0,则不做处理
4、若m == 0 or 扫描结束,退出循环。
代码实现,也不难,如下:
//copyright@ 2011 yansha //July、updated,2011.04.25。 #include <iostream> #include <string> using namespace std; int main() { string str1="ABCDEFGHLMNOPQRS"; string str2="DCGSRQPOM"; // 开辟一个辅助数组并清零 int hash[26] = {0}; // num为辅助数组中元素个数 int num = 0; // 扫描短字符串 for (int j = 0; j < str2.length(); j++) { // 将字符转换成对应辅助数组中的索引 int index = str1[j] - 'A'; // 如果辅助数组中该索引对应元素为0,则置1,且num++; if (hash[index] == 0) { hash[index] = 1; num++; } } // 扫描长字符串 for (int k = 0; k < str1.length(); k++) { int index = str1[k] - 'A'; // 如果辅助数组中该索引对应元素为1,则num--;为零的话,不作处理(不写语句)。 if(hash[index] ==1) { hash[index] = 0; num--; if(num == 0) //m==0,即退出循环。 break; } } // num为0说明长字符串包含短字符串内所有字符 if (num == 0) cout << "true" << endl; else cout << "false" << endl; return 0; }
2.2、O(n+m)的数组存储方法
有两个字符串short_str和long_str。
第一步:你标记short_str中有哪些字符,在store数组中标记为true。(store数组起一个映射的作用,如果有A,则将第1个单元标记true,如果有B,则将第2个单元标记true,... 如果有Z, 则将第26个单元标记true)
第二步:遍历long_str,如果long_str中的字符包括short_str中的字符则将store数组中对应位置标记为false。(如果有A,则将第1个单元标记false,如果有B,则将第2个单元标记false,... 如果有Z, 则将第26个单元标记false),如果没有,则不作处理。
第三步:此后,遍历store数组,如果所有的元素都是false,也就说明store_str中字符都包含在long_str内,输出true。否则,输出false。
举个简单的例子好了,如abcd,abcdefg俩个字符串,
1、先遍历短字符串abcd,在store数组中想对应的abcd的位置上的单元元素置为true,
2、然后遍历abcdefg,在store数组中相应的abcd位置上,发现已经有了abcd,则前4个的单元元素都置为false,当我们已经遍历了4个元素,等于了短字符串abcd的4个数目,所以,满足条件,退出。
(不然,继续遍历的话,我们会发现efg在store数组中没有元素,不作处理。最后,自然,就会发现store数组中的元素单元都是false的。)
3、遍历store数组,发现所有的元素都已被置为false,所以程序输出true。
其实,这个思路和上一节中,O(n+m)的hashtable的方法代码,原理是完全一致的,且本质上都采用的数组存储(hash表也是一个数组),但我并不认为此思路多此一举,所以仍然贴出来。ok,代码如下://copyright@ 2011 Hession //July、updated,2011.04.23. #include<iostream> #include<string.h> using namespace std; int main() { char long_ch[]="ABCDEFGHLMNOPQRS"; char short_ch[]="DEFGHXLMNOPQ"; int i; bool store[58]; memset(store,false,58); //前两个 是 遍历 两个字符串, 后面一个是 遍历 数组 for(i=0;i<sizeof(short_ch)-1;i++) store[short_ch[i]-65]=true; for(i=0;i<sizeof(long_ch)-1;i++) { if(store[long_ch[i]-65]!=false) store[long_ch[i]-65]=false; } for(i=0;i<58;i++) { if(store[i]!=false) { cout<<"short_ch is not in long_ch"<<endl; break; } if(i==57) cout<<"short_ch is in long_ch"<<endl; } return 0; }
第三节、O(n)到O(n+m)的素数方法
我想问的是,还有更好的方案么?
你可能会这么想:O(n+m)是你能得到的最好的结果了,至少要对每个字母至少访问一次才能完成这项操作,而上一节最后的俩个方案是刚好是对每个字母只访问一次。
ok,下面给出一个更好的方案:
假设我们有一个一定个数的字母组成字串,我给每个字母分配一个素数,从2开始,往后类推。这样A将会是2,B将会是3,C将会是5,等等。现在我遍历第一个字串,把每个字母代表的素数相乘。你最终会得到一个很大的整数,对吧?
然后——轮询第二个字符串,用每个字母除它。如果除的结果有余数,这说明有不匹配的字母。如果整个过程中没有余数,你应该知道它是第一个字串恰好的子集了。
思路总结如下:
1.定义最小的26个素数分别与字符'A'到'Z'对应。
2.遍历长字符串,求得每个字符对应素数的乘积。
3.遍历短字符串,判断乘积能否被短字符串中的字符对应的素数整除。
4.输出结果。
至此,如上所述,上述算法的时间复杂度为O(m+n),时间复杂度最好的情况为O(n)(遍历短的字符串的第一个数,与长字符串素数的乘积相除,即出现余数,便可退出程序,返回false),n为长字串的长度,空间复杂度为O(1)。如你所见,我们已经优化到了最好的程度。
不过,正如原文中所述:“现在我想告诉你 —— Guy的方案(不消说,我并不认为Guy是第一个想出这招的人)在算法上并不能说就比我的好。而且在实际操作中,你很可能仍会使用我的方案,因为它更通用,无需跟麻烦的大型数字打交道。但从”巧妙水平“上讲,Guy提供的是一种更、更、更有趣的方案。”
ok,如果你有更好的思路,欢迎在本文的评论中给出,非常感谢。#include <iostream> #include <string> #include "BigInt.h" using namespace std; // 素数数组 int primeNumber[26] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101}; int main() { string strOne = "ABCDEFGHLMNOPQRS"; string strTwo = "DCGSRQPOM"; // 这里需要用到大整数 CBigInt product = 1; //大整数除法的代码,下头给出。 // 遍历长字符串,得到每个字符对应素数的乘积 for (int i = 0; i < strOne.length(); i++) { int index = strOne[i] - 'A'; product = product * primeNumber[index]; } // 遍历短字符串 for (int j = 0; j < strTwo.length(); j++) { int index = strTwo[j] - 'A'; // 如果余数不为0,说明不包括短字串中的字符,跳出循环 if (product % primeNumber[index] != 0) break; } // 如果积能整除短字符串中所有字符则输出"true",否则输出"false"。 if (strTwo.length() == j) cout << "true" << endl; else cout << "false" << endl; return 0; } 上述程序待改进的地方:
1.只考虑大些字符,如果考虑小写字符和数组的话,素数数组需要更多素数
2.没有考虑重复的字符,可以加入判断重复字符的辅助数组。
以下的大整数除法的代码,虽然与本题目无多大关系,但为了保证文章的完整性,我还是决定把它贴出来,
代码如下(点击展开):
//copyright@ 2011/03/06 yansha //实现大整数类 #include <string> #include <vector> #include <iostream> using namespace std; class CBigInt { public: // input friend istream& operator >> (istream &, CBigInt &); // output friend ostream& operator << (ostream &os, const CBigInt &value) { if (value.bigInt[0] == '-') os << value.bigInt; else { // 正数不输出符号 os << value.bigInt.substr(1); } return os; } friend bool operator == (const CBigInt &, const CBigInt &); friend bool operator < (const CBigInt &lValue, const CBigInt &rValue) { if (lValue.bigInt[0] != rValue.bigInt[0]) { // '+'ASCII码为43,'-'ASCII码为45 return lValue.bigInt[0] > rValue.bigInt[0]; } else { if (lValue.bigInt[0] == '+') return lValue.smaller(rValue.bigInt); // 正数的情况 else return lValue.greater(rValue.bigInt); // 负数的情况 } } friend bool operator > (const CBigInt &lValue, const CBigInt &rValue) { if (lValue.bigInt[0] != rValue.bigInt[0]) return lValue.bigInt[0] < rValue.bigInt[0]; else { if (lValue.bigInt[0] == '+') return lValue.greater(rValue.bigInt); else return lValue.smaller(rValue.bigInt); } } string bigInt; public: CBigInt(); CBigInt(int); CBigInt(const string &); CBigInt(const CBigInt &); CBigInt(const char *); CBigInt& operator = (const CBigInt &); CBigInt& operator += (const CBigInt &); CBigInt& operator -= (const CBigInt &); CBigInt& operator *= (const CBigInt &); CBigInt& operator /= (const CBigInt &); CBigInt& operator %= (const CBigInt &); // prefix increment CBigInt& operator ++ (); // prefix decrement CBigInt& operator -- (); // postfix increment CBigInt operator ++ (int); // postfix decrement CBigInt operator -- (int); private: // unsigned += void plus(const string &); // unsigned -= void minus(const string &); // unsigned == bool equal(const string &) const; // unsigned < bool smaller(const string &) const; // unsigned > bool greater(const string &) const; }; /************************************************************************/ /* 构造函数 /************************************************************************/ // 默认构造函数 inline CBigInt::CBigInt() : bigInt("+0") {} // 构造函数 inline CBigInt::CBigInt(const string &str) : bigInt(str) { if (bigInt.size() > 0) { // 没有正负符号 if (bigInt[0] != '+' && bigInt[0] != '-') { string::size_type i = 0; for (; i < bigInt.size() - 1 && bigInt[i] == '0'; i++); if (i > 0) bigInt.replace((string::size_type)0, i, "+"); else bigInt.insert((string::size_type)0, 1, '+'); } else { if (bigInt.size() == 1) bigInt = "+0"; else { string::size_type j = 1; // 去掉多余的0 for (; j < bigInt.size() - 1 && bigInt[j] == '0'; j++); if (j > 1) bigInt.erase((string::size_type)1, j - 1); if (bigInt == "-0") bigInt = "+0"; } } } else bigInt = "+0"; } // 复制构造函数 inline CBigInt::CBigInt(const CBigInt &value) : bigInt(value.bigInt) {} inline CBigInt::CBigInt(int num) { if (num == 0) bigInt = "+0"; else if (num > 0) bigInt = '+'; else { bigInt = '-'; num *= -1; } string temp = ""; while (num != 0) { temp += num % 10 + '0'; num = num / 10; } for (int i = temp.size() - 1; i >= 0; i--) bigInt += temp[i]; } inline CBigInt::CBigInt(const char *str) : bigInt(str) { if (bigInt.size() > 0) { if (bigInt[0] != '+' && bigInt[0] != '-') { string::size_type i = 0; // 去除多余的0 for (; i < bigInt.size() - 1 && bigInt[i] == '0'; i++); if (i > 0) bigInt.replace((string::size_type)0, i, "+"); else bigInt.insert((string::size_type)0, 1, '+'); } else { if (bigInt.size() == 0) bigInt = "+0"; else { string::size_type j = 1; for (; j < bigInt.size() - 1 && bigInt[j] == '0'; j++); if (j > 1) bigInt.erase((string::size_type)1, j - 1); // 处理特殊情况“-0” if (bigInt == "-0") bigInt = "+0"; } } } else bigInt = "+0"; } inline bool operator == (const CBigInt &lValue, const CBigInt &rValue) { return lValue.bigInt == rValue.bigInt; } inline bool operator != (const CBigInt &lValue, const CBigInt &rValue) { return !(lValue.bigInt == rValue.bigInt); } inline bool operator <= (const CBigInt &lValue, const CBigInt &rValue) { return !(lValue > rValue); } inline bool operator >= (const CBigInt &lValue, const CBigInt &rValue) { return !(lValue < rValue); } inline CBigInt& CBigInt::operator = (const CBigInt &value) { bigInt = value.bigInt; return *this; } // unsigned == inline bool CBigInt::equal(const string &value) const { return bigInt.substr(1) == value.substr(1); } // unsigned < inline bool CBigInt::smaller(const string &value) const { if (bigInt.size() == value.size()) return bigInt.substr(1) < value.substr(1); else return bigInt.size() < value.size(); } // unsigned > inline bool CBigInt::greater(const string &value) const { if (bigInt.size() == value.size()) return bigInt.substr(1) > value.substr(1); else return bigInt.size() > value.size(); } /************************************************************************/ /* 实现+,-,*,/运算 /************************************************************************/ void CBigInt::plus(const string &value) { if (bigInt.size() < value.size()) bigInt.insert((string::size_type)1, (value.size() - bigInt.size()), '0'); string::size_type i = bigInt.size() - 1; string::size_type j = value.size() - 1; while (j > 1) { bigInt[i] += value[j] - '0'; if (bigInt[i] > '9') { bigInt[i] -= 10; ++bigInt[i-1]; } i--; j--; } // 最高位进位 bigInt[i] += value[1] - '0'; while (i > 1 && bigInt[i] > '9') { bigInt[i] -= 10; i--; ++bigInt[i]; } if (bigInt[1] > '9') { bigInt[1] -= 10; bigInt.insert((string::size_type)1, 1, '1'); } } void CBigInt::minus(const string &vlaue) { string::size_type i = bigInt.size() - 1; string::size_type j = vlaue.size() - 1; while (j >= 1) { bigInt[i] -= vlaue[j] - '0'; if (bigInt[i] < '0') { bigInt[i] += 10; --bigInt[i-1]; } i--; j--; } // 向前借位 while (i > 1 && bigInt[i] < '0') { bigInt[i] += 10; i--; --bigInt[i]; } // 去除多余的0 string::size_type k = 1; for (; k < bigInt.size() - 1 && bigInt[k] == '0'; k++); if (k > 1) bigInt.erase((string::size_type)1, k - 1); } CBigInt& CBigInt::operator += (const CBigInt &value) { if (bigInt[0] == value.bigInt[0]) plus(value.bigInt); else { // 互为相反数的情况 if (equal(value.bigInt)) bigInt = "+0"; // 绝对值小于的情况 else if (smaller(value.bigInt)) { string temp = bigInt; bigInt = value.bigInt; minus(temp); } else minus(value.bigInt); } return *this; } CBigInt& CBigInt::operator -= (const CBigInt &value) { // 处理过程与+=类似 if (bigInt[0] == value.bigInt[0]) { if (equal(value.bigInt)) bigInt = "+0"; else if (smaller(value.bigInt)) { string temp = bigInt; bigInt = value.bigInt; minus(temp); if (bigInt[0] == '+') bigInt[0] = '-'; else bigInt[0] = '+'; } else minus(value.bigInt); } else plus(value.bigInt); return *this; } CBigInt operator + (const CBigInt &lValue, const CBigInt &rValue) { CBigInt sum(lValue); sum += rValue; return sum; } CBigInt operator - (const CBigInt &lValue, const CBigInt &rValue) { CBigInt diff(lValue); diff -= rValue; return diff; } // prefix increment CBigInt& CBigInt::operator ++ () { string::size_type i = bigInt.size() - 1; if (bigInt[0] == '+') { ++bigInt[i]; while (i > 1 && bigInt[i] > '9') { bigInt[i] -= 10; i--; ++bigInt[i]; } if (bigInt[i] > '9') { bigInt[i] -= 10; bigInt.insert((string::size_type)1, 1, '1'); } } else { --bigInt[i]; while(i > 1 && bigInt[i] < '0') { bigInt[i] += 10; i--; --bigInt[i]; } string::size_type j = 1; for (; j < bigInt.size() - 1 && bigInt[j] == '0'; j++); if (j > 1) bigInt.erase(1, j - 1); if (bigInt[1] == '0') bigInt[0] = '+'; } return *this; } CBigInt& CBigInt::operator -- () { string::size_type i = bigInt.size() - 1; // 对正数和负数分别处理 if (bigInt[0] == '+') { // 对0进行处理 if (bigInt[1] == '0') bigInt = "-1"; else { --bigInt[i]; while (i > 1 && bigInt[i] < '0') { bigInt[i] += 10; i--; --bigInt[i]; } string::size_type j = 1; for (; j < bigInt.size() - 1 && bigInt[j] == '0'; j++); if (j > 1) bigInt.erase(1, j - 1); } } else { ++bigInt[i]; while (i > 1 && bigInt[i] > '9') { bigInt[i] -= 10; i--; ++bigInt[i]; } if (bigInt[1] > '9') { bigInt[1] += 10; bigInt.insert((string::size_type)1, 1, '1'); } } return *this; } // postfix increment CBigInt CBigInt::operator ++ (int) { CBigInt temp(*this); ++(*this); return temp; } // postfix decrement CBigInt CBigInt::operator -- (int) { CBigInt temp(*this); --(*this); return temp; } // 模拟笔算过程 CBigInt& CBigInt::operator *= (const CBigInt &value) { // 乘数或被乘数有一方为0则返回结果0 if (bigInt[1] == '0' || value.bigInt[1] == '0') { bigInt = "+0"; return *this; } string::size_type sizeofMultiplicand = bigInt.size(); string::size_type sizeofMultiplier = value.bigInt.size(); vector<unsigned int> product(sizeofMultiplier + sizeofMultiplicand - 1); // 初始化 for (string::size_type i = 1; i < sizeofMultiplicand; ++i) bigInt[i] -= '0'; // 笔算乘法过程 for (string::size_type j = sizeofMultiplier - 1; j > 0; --j) { if (value.bigInt[j] > '0') { for (string::size_type k = sizeofMultiplicand - 1; k > 0; --k) product[k+j] += bigInt[k] * (value.bigInt[j] - '0'); } } // 处理符号 if (bigInt[0] == value.bigInt[0]) product[0] = '+'; else product[0] = '-'; vector<unsigned int>::size_type sizeofProduct = product.size(); bigInt = string(sizeofProduct, '0'); bigInt[0] = product[0]; // 处理进位问题 for (vector<unsigned int>::size_type n = sizeofProduct - 1; n > 1; --n) { product[n-1] += product[n] / 10; product[n] %= 10; bigInt[n] += product[n]; } if (product[1] == 0) bigInt.erase(1, 1); else bigInt[1] += product[1]; return *this; } // 重复做差法求商 CBigInt& CBigInt::operator /= (const CBigInt &value) { // 除数为0 if (value.bigInt == "+0") { bigInt = "*Error!"; return *this; } // 被除数大于除数 if (value.smaller(bigInt) == true) { string::size_type sizeofDividend = bigInt.size(); string::size_type sizeofDivisor = value.bigInt.size(); string answer(sizeofDividend, '0'); // 符号处理 if (bigInt[0] == value.bigInt[0]) answer[0] = '+'; else answer[0] = '-'; string::size_type start = 1; string::size_type end = sizeofDivisor - 1; while (end < sizeofDividend) { // 试商过程,从高位到低位 while (value.greater(bigInt.substr(start - 1, end - start + 2)) == false) { string::size_type j = end; // 减法过程 for (string::size_type i = sizeofDivisor - 1; i > 0; i--, j--) { bigInt[j] -= value.bigInt[i] - '0'; if (bigInt[j] < '0') { bigInt[j] += 10; --bigInt[j-1]; } } // 商的相应位加1 ++answer[end]; // 以除数做边界去掉前缀0 while (start <= end && bigInt[start] == '0') ++start; } // 以被除数做边界去掉前缀0 while (start < sizeofDividend && bigInt[start] == '0') ++start; // 如果end-start+1 < sizeofDivisor - 1,则进行补位 if (end - start + 2 < sizeofDivisor) end = sizeofDivisor + start - 2; else ++end; } start = 1; for (; start < answer.size() - 1 && answer[start] == '0'; ++start); if (start > 1) answer.erase(1, start - 1); bigInt = answer; } // 绝对值相等的情况 else if (value.equal(bigInt) == true) { string answer = "-1"; if (bigInt[0] == value.bigInt[0]) answer = "+1"; bigInt = answer; } else bigInt = "+0"; return *this; } // 求余,与上面去商过程基本一致 CBigInt& CBigInt::operator %= (const CBigInt &value) { if (value.bigInt == "+0") { bigInt = "*Error!"; return *this; } // 求余,余数为剩余bigInt值 if (value.smaller(bigInt) == true) { string::size_type sizeofDivident = bigInt.size(); string::size_type sizeofDivisor = value.bigInt.size(); string::size_type start = 1; string::size_type end = sizeofDivisor - 1; while (end < sizeofDivident) { // 除数的值不大于被除数的值 while (value.greater(bigInt.substr(start - 1, end - start + 2)) == false) { string::size_type j = end; for (string::size_type i = sizeofDivisor - 1; i > 0; --i, --j) { bigInt[j] -= value.bigInt[i] - '0'; if (bigInt[j] < '0') { bigInt[j] += 10; --bigInt[j-1]; } } while (start <= end && bigInt[start] == '0') ++start; } while (start < sizeofDivident && bigInt[start] == '0') ++start; if (end - start + 2 < sizeofDivisor) end = sizeofDivisor + start - 2; else ++end; } start = 1; for (; start < sizeofDivident - 1 && bigInt[start] == '0'; start++); if (start > 1) bigInt.erase(1, start - 1); if (bigInt == "-0") bigInt[0] = '+'; } else if (value.equal(bigInt)) bigInt = "+0"; return *this; } CBigInt operator * (const CBigInt &lValue, const CBigInt &rValue) { CBigInt product(lValue); product *= rValue; return product; } CBigInt operator / (const CBigInt &lValue, const CBigInt &rValue) { CBigInt quotient(lValue); quotient /= rValue; return quotient; } CBigInt operator % (const CBigInt &lValue, const CBigInt &rValue) { CBigInt mod(lValue); mod %= rValue; return mod; }
说明:此次的判断字符串是否包含问题,来自一位外国网友提供的gofish、google面试题,这个题目出自此篇文章:http://www.aqee.net/2011/04/11/google-interviewing-story/,文章记录了整个面试的过程,比较有趣,值得一读。
扩展:正如网友安逸所说:其实这个问题还可以转换为:a和b两个字符串,求b串包含a串的最小长度。包含指的就是b的字串包含a中每个字符。
第四节、字符串是否包含问题的继续补充
updated:本文发布后,得到很多朋友的建议和意见,其中nossiac,luuillu等俩位网友除了给出具体的思路之外,还给出了代码,征得同意,下面,我将引用他们的的思路及代码,继续就这个字符串是否包含问题深入阐述。
4.1、在引用nossiac的思路之前,我得先给你介绍下什么是Bit-map?
Oliver:所谓的Bit-map就是用一个bit位来标记某个元素对应的Value, 而Key即是该元素。由于采用了Bit为单位来存储数据,因此在存储空间方面,可以大大节省。
如果看了以上说的还没明白什么是Bit-map,那么我们来看一个具体的例子,假设我们要对0-7内的5个元素(4,7,2,5,3)排序(这里假设这些元素没有重复)。那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数,我们就只需要8个Bit(1Bytes),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0,如下图:

然后遍历这5个元素,首先第一个元素是4,那么就把4对应的位置为1(可以这样操作:p+(i/8)|(0x01<<(i%8))当然了这里的操作涉及到Big-ending和Little-ending的情况,这里默认为Big-ending),因为是从零开始的,所以要把第五位置为一(如下图):
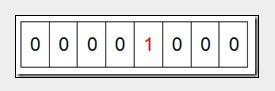
接着再处理第二个元素7,将第八位置为1,,接着再处理第三个元素,一直到最后处理完所有的元素,将相应的位置为1,这时候的内存的Bit位的状态如下:
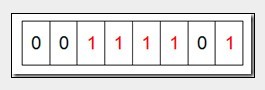
最后我们现在遍历一遍Bit区域,将该位是一的位的编号输出(2,3,4,5,7),这样就达到了排序的目的。
代码示例:
//位图的一个示例 //copyright@ Oliver && July //http://blog.redfox66.com/post/2010/09/26/mass-data-4-bitmap.aspx //July、updated,2011.04.25. #include <memory.h> #include <stdio.h> //定义每个Byte中有8个Bit位 #define BYTESIZE 8 void SetBit(char *p, int posi) { for(int i=0; i < (posi/BYTESIZE); i++) { p++; } *p = *p|(0x01<<(posi%BYTESIZE)); //将该Bit位赋值1 return; } void BitMapSortDemo() { //为了简单起见,我们不考虑负数 int num[] = {3,5,2,10,6,12,8,14,9}; //BufferLen这个值是根据待排序的数据中最大值确定的 //待排序中的最大值是14,因此只需要2个Bytes(16个Bit) //就可以了。 const int BufferLen = 2; char *pBuffer = new char[BufferLen]; //要将所有的Bit位置为0,否则结果不可预知。 memset(pBuffer,0,BufferLen); for(int i=0;i<9;i++) { //首先将相应Bit位上置为1 SetBit(pBuffer,num[i]); } //输出排序结果 for(i=0;i<BufferLen;i++) //每次处理一个字节(Byte) { for(int j=0;j<BYTESIZE;j++) //处理该字节中的每个Bit位 { //判断该位上是否是1,进行输出,这里的判断比较笨。 //首先得到该第j位的掩码(0x01<<j),将内存区中的 //位和此掩码作与操作。最后判断掩码是否和处理后的 //结果相同 if((*pBuffer&(0x01<<j)) == (0x01<<j)) { printf("%d ",i*BYTESIZE + j); } } pBuffer++; } printf("\n"); } int main() { BitMapSortDemo(); return 0; }
位图总结:
1、可进行数据的快速查找,判重,删除,一般来说数据范围是int的10倍以下
2、使用bit数组来表示某些元素是否存在,比如8位电话号码
3、Bloom filter(日后介绍)可以看做是对bit-map的扩展
问题实例:
1)已知某个文件内包含一些电话号码,每个号码为8位数字,统计不同号码的个数。
8位最多99 999 999,大概需要99m个bit,大概10几m字节的内存即可。 (可以理解为从0-99 999 999的数字,每个数字对应一个Bit位,所以只需要99M个Bit==12MBytes,这样,就用了小小的12M左右的内存表示了所有的8位数的电话)
2)2.5亿个整数中找出不重复的整数的个数,内存空间不足以容纳这2.5亿个整数。
将bit-map扩展一下,用2bit表示一个数即可,0表示未出现,1表示出现一次,2表示出现2次及以上,在遍历这些数的时候,如果对应位置的值是0,则将其置为1;如果是1,将其置为2;如果是2,则保持不变。或者我们不用2bit来进行表示,我们用两个bit-map即可模拟实现这个2bit-map,都是一样的道理。
ok,介绍完了什么是bit-map,接下来,咱们回到正题,来看下nossiac关于此字符串是否包含问题的思路(http://www.shello.name/me/?p=64):
每个字母的ASCII码值,可以对应一个位图中的位。
先遍历第一个字符串,生成一个“位图字典”。
用伪代码表示就是:
dictionary = 0
for x in String1:
dictionary |= 0x01<<x-'a'
红色部分就是构造位图字典的过程,刚好能运用ASCII码值完成,取巧,呵呵,比较惬意。
然后,我们遍历第二个字符串,用查字典的方式较检,伪代码为:
for x in String2:
if dictionary != dictionary|0x01<<x-'a':
print("NO")
else:
print("YES")
what?还不够明白,ok,看yansha对此思路的具体阐述吧:
此思路是位操作的典型应用:
dictionary = 0
for x in String1:
dictionary |= 0x01 << (x - 'a');
分析如下:
dictionary是一个32位的int,初始化为0
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
dictionary |= 0x01 << (x - 'a')则是把字符映射到dictionary当中的某一位;
比方String1 = "abde";
1、当x为‘a’时,x-‘a’为0,所以0x01<<0 为0x01。
那么dictionary |= 0x01,也就是将dictionary的第一位置1。
此时dictionary为:
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
2、当x为‘b’时,x-‘b’为1,所以0x01<<1 为0x02。
那么dictionary |= 0x02,也就是将dictionary的第二位置1。
此时dictionary为:
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
3、当x为‘d’时,x-‘d’为3,所以0x01<<3 为0x08。
那么dictionary |= 0x08,也就是将dictionary的第四位置1。
此时dictionary为:
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
4、当x为‘e’时,x-‘e’为4,所以0x01<<4 为0x10。
那么dictionary |= 0x10,也就是将dictionary的第五位置1。
此时dictionary为:
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
其他字符依此类推,比较过程也类似。对于128个字符的ASCII码而言,显然一个32位的整形是不够的。
OK,算法完成。时间复杂度为 O(m+n),空间复杂度为O(1)。
然后,代码可以编写如下:
//copyright@ nossiac //July、updated,2011.04.24。 #include <stdio.h> #include <string.h> #define getbit(x) (1<<(x-'a')) void a_has_b(char * a, char * b) { int i = 0; int dictionary = 0; int alen = strlen(a); int blen = strlen(b); for(i=0;i<alen;i++) dictionary |= getbit(a[i]); for(i=0;i<blen;i++) { if(dictionary != (dictionary|getbit(b[i]))) break; } if(i==blen) printf("YES! A has B!\n"); else printf("NiO! Char at %d is not found in dictionary!\n",i); } int main() { char * str1="abcdefghijklmnopqrstuvwxyz"; char * str2="akjsdfasdfiasdflasdfjklffhasdfasdfjklasdfjkasdf"; char * str3="asdffaxcfsf"; char * str4="asdfai"; a_has_b(str1, str2); a_has_b(str1, str3); a_has_b(str3, str4); return 0; }
4.2、还可以如luuillu所说,判断字符串是否包含,采用移位的方法(此帖子第745楼:http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9_8.html?seed=423056362&r=72955051#r_72955051),他的代码编写如下://copyright@ luuillu //July、updated,2011.04.24。 #include <iostream> using namespace std; //判断 des 是否包含在 src 中 bool compare(char *des,char * src) { unsigned index[26]={1,2,4,8,16,32,64,128,256,512,1024,1<<11, 1<<12,1<<13,1<<14,1<<15,1<<16,1<<17,1<<18,1<<19, 1<<20,1<<21,1<<22,1<<23,1<<24,1<<25}; //2的n次幂 unsigned srcdata=0; unsigned desdata=0; while( *src) srcdata|=index[(*src++)-'A']; while(*des) desdata|=index[(*des++)-'A']; return (srcdata|desdata) == srcdata ; } int main() { char *src="ABCDEFGHLMNOPQRS"; char *des="DCGSRQPOM"; cout<<compare(des,src)<<endl; return 0; }
第四节总结:正如十一文章在本文评论里所提到的那样,上面的位图法,hash,还有bitmap三者之间并没有本质上的区别,只是形式上不同而已。
第五节、字符串相关问题扩展与阐述
5.1、字符串匹配问题
题目描述:
假设两个字符串中所含有的字符和个数都相同我们就叫这两个字符串匹配,比如:abcda和adabc,
由于出现的字符个数都是相同,只是顺序不同,所以这两个字符串是匹配的。
要求高效实现下面的函数: boolen Is_Match(char *str1,char *str2)。
分析:可以看出,此字符串的匹配问题,是与上述字符串包含的问题相类似的,这个问题可以先排序再比较,也可以利用hash表进行判断。这里给出一种hash表的方法,原理已在上文中阐明了,代码如下://copyright@ 2011 yansha //July、updated,2011.04.24。 #include <iostream> #include <string> using namespace std; bool Is_Match(const char *strOne,const char *strTwo) { int lenOfOne = strlen(strOne); int lenOfTwo = strlen(strTwo); // 如果长度不相等则返回false if (lenOfOne != lenOfTwo) return false; // 开辟一个辅助数组并清零 int hash[26] = {0}; // 扫描字符串 for (int i = 0; i < strlen(strOne); i++) { // 将字符转换成对应辅助数组中的索引 int index = strOne[i] - 'A'; // 辅助数组中该索引对应元素加1,表示该字符的个数 hash[index]++; } // 扫描字符串 for (int j = 0; j < strlen(strTwo); j++) { int index = strTwo[j] - 'A'; // 如果辅助数组中该索引对应元素不为0则减1,否则返回false if (hash[index] != 0) hash[index]--; else return false; } return true; } int main() { string strOne = "ABBA"; string strTwo = "BBAA"; bool flag = Is_Match(strOne.c_str(), strTwo.c_str()); // 如果为true则匹配,否则不匹配 if (flag == true) cout << "Match" << endl; else cout << "No Match" << endl; return 0; }
5.2、在字符串中查找子串
题目描述:
给定一个字符串A,要求在A中查找一个子串B。
如A="ABCDF",要你在A中查找子串B=“CD”。
分析:比较简单,相当于实现strstr库函数,主体代码如下://copyright@ 2011 July && luoqitai //string为模式串,substring为要查找的子串 int strstr(char *string,char *substring) { int len1=strlen(string); int len2=strlen(substring); for (int i=0; i<=len1-len2; i++) //复杂度为O(m*n) { for (int j=0; j<len2; j++) { if (string[i+j]!=substring[j]) break; } if (j==len2) return i+1; } return 0; }
上述程序已经实现了在字符串中查找第一个子串的功能,时间复杂度为O(n*m),继续的优化可以先对两个字符串进行排序,然后再查找,也可以用KMP算法,复杂度为O(m+n)。具体的,在此不再赘述(多谢hlm_87指正)。
扩展:还有个类似的问题:第17题(字符串):题目:在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b。代码,可编写如下(测试正确):
#include <iostream> using namespace std; //查找第一个只出现一次的字符,第1个程序 //copyright@ Sorehead && July //July、updated,2011.04.24. char find_first_unique_char(char *str) { int data[256]; char *p; if (str == NULL) return '\0'; memset(data, 0, sizeof(data)); //数组元素先全部初始化为0 p = str; while (*p != '\0') data[(unsigned char)*p++]++; //遍历字符串,在相应位置++,(同时,下标强制转换) while (*str != '\0') { if (data[(unsigned char)*str] == 1) //最后,输出那个第一个只出现次数为1的字符 return *str; str++; } return '\0'; } int main() { char *str = "afaccde"; cout << find_first_unique_char(str) << endl; return 0; } 当然,代码也可以这么写(测试正确):
//查找第一个只出现一次的字符,第2个程序 //copyright@ yansha //July、updated,2011.04.24. char FirstNotRepeatChar(char* pString) { if(!pString) return '\0'; const int tableSize = 256; int hashTable[tableSize] = {0}; //存入数组,并初始化为0 char* pHashKey = pString; while(*(pHashKey) != '\0') hashTable[*(pHashKey++)]++; while(*pString != '\0') { if(hashTable[*pString] == 1) return *pString; pString++; } return '\0'; //没有找到满足条件的字符,退出 }
5.3、字符串转换为整数
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
分析:此题看起来,比较简单,每扫描到一个字符,我们把在之前得到的数字乘以10再加上当前字符表示的数字。这个思路用循环不难实现。然其背后却隐藏着不少陷阱,正如zhedahht 所说,有以下几点需要你注意:
1、由于整数可能不仅仅之含有数字,还有可能以'+'或者'-'开头,表示整数的正负。如果第一个字符是'+'号,则不需要做任何操作;如果第一个字符是'-'号,则表明这个整数是个负数,在最后的时候我们要把得到的数值变成负数。
2、如果使用的是指针的话,在使用指针之前,我们要做的第一件是判断这个指针是不是为空。如果试着去访问空指针,将不可避免地导致程序崩溃(此第2点在下面的程序不需注意,因为没有用到指针)。
3、输入的字符串中可能含有不是数字的字符。
每当碰到这些非法的字符,我们就没有必要再继续转换。
4、溢出问题。由于输入的数字是以字符串的形式输入,因此有可能输入一个很大的数字转换之后会超过能够表示的最大的整数而溢出。
总结以上四点,代码可以如下编写:
//字符串转换为整数 //copyright@ yansha #include <iostream> #include <string> using namespace std; int str_2_int(string str) { if (str.size() == 0) exit(0); int pos = 0; int sym = 1; // 处理符号 if (str[pos] == '+') pos++; else if (str[pos] == '-') { pos++; sym = -1; } int num = 0; // 逐位处理 while (pos < str.length()) { // 处理数字以外的字符 if (str[pos] < '0' || str[pos] > '9') exit(0); num = num * 10 + (str[pos] - '0'); // 处理溢出 if (num < 0) exit(0); pos++; } num *= sym; return num; } int main() { string str = "-3450"; int num = str_2_int(str); cout << num << endl; return 0; }
@helloword:这个的实现非常不好,当输入字符串参数为非法时,不是抛出异常不是返回error code,而是直接exit了。直接把进程给终止了,想必现实应用中的实现都不会这样。建议您改改,不然拿到面试官那,会被人喷死的。ok,听从他的建议,借用zhedahht的代码了:
//http://zhedahht.blog.163.com/blog/static/25411174200731139971/ enum Status {kValid = 0, kInvalid}; int g_nStatus = kValid; int StrToInt(const char* str) { g_nStatus = kInvalid; long long num = 0; if(str != NULL) { const char* digit = str; // the first char in the string maybe '+' or '-' bool minus = false; if(*digit == '+') digit ++; else if(*digit == '-') { digit ++; minus = true; } // the remaining chars in the string while(*digit != '\0') { if(*digit >= '0' && *digit <= '9') { num = num * 10 + (*digit - '0'); // overflow if(num > std::numeric_limits<int>::max()) { num = 0; break; } digit ++; } // if the char is not a digit, invalid input else { num = 0; break; } } if(*digit == '\0') { g_nStatus = kValid; if(minus) num = 0 - num; } } return static_cast<int>(num); }
updated:
yansha看到了上述helloword的所说的后,修改如下:
#include <iostream> #include <string> #include <assert.h> using namespace std; int str_2_int(string str) { assert(str.size() > 0); int pos = 0; int sym = 1; // 处理符号 if (str[pos] == '+') pos++; else if (str[pos] == '-') { pos++; sym = -1; } int num = 0; // 逐位处理 while (pos < str.length()) { // 处理数字以外的字符 assert(str[pos] >= '0'); assert(str[pos] <= '9'); num = num * 10 + (str[pos] - '0'); // 处理溢出 assert(num >= 0); pos++; } num *= sym; return num; } int main() { string str = "-1024"; int num = str_2_int(str); cout << num << endl; return 0; }
5.4、字符串拷贝
题目描述:
要求实现库函数strcpy,
原型声明:extern char *strcpy(char *dest,char *src);
功能:把src所指由NULL结束的字符串复制到dest所指的数组中。
说明:src和dest所指内存区域不可以重叠且dest必须有足够的空间来容纳src的字符串。
返回指向dest的指针。
分析:如果编写一个标准strcpy函数的总分值为10,下面给出几个不同得分的答案://2分 void strcpy( char *strDest, char *strSrc ) { while( (*strDest++ = * strSrc++) != '\0' ); } //4分 void strcpy( char *strDest, const char *strSrc ) { //将源字符串加const,表明其为输入参数,加2分 while( (*strDest++ = * strSrc++) != '\0' ); } //7分 void strcpy(char *strDest, const char *strSrc) { //对源地址和目的地址加非0断言,加3分 assert( (strDest != NULL) && (strSrc != NULL) ); while( (*strDest++ = * strSrc++) != '\0' ); } //10分 //为了实现链式操作,将目的地址返回,加3分! char * strcpy( char *strDest, const char *strSrc ) { assert( (strDest != NULL) && (strSrc != NULL) ); char *address = strDest; while( (*strDest++ = * strSrc++) != '\0' ); return address; }
联系作者:
微博:http://weibo.com/julyweibo @ July,http://weibo.com/yanshazi @ yansha。
邮箱:zhoulei0907@yahoo.cn @ July,yansha0@hotmail.com @ yansha。
预告:程序员面试题狂想曲、第三章,4月底之前发布。
ok,以上,有任何问题,欢迎任何人不吝指正。谢谢。完。
版权声明:1、严禁用于任何商业用途;2、未经许可,严禁出版;3、转载,务必注明出处。




)














)