注:以下来自《C++数值算法一书》,仅对章节内容做摘要,为的是给自己扫盲,不涉及算法。
这里只讨论一些最清晰明了的一般方法。
1. 级数与其收敛性
思想:解析函数可在某点x0的邻域内展开成级数:![]() 。用这个级数可以直接估值。对于通项的模是递减的级数,可以用艾肯特δ2过程加速收敛。对交错级数(和式中项的符号交替变化),欧拉变换是强大的工具。van Wijngaarden方法是欧拉变换的一个精巧的实现方式。
。用这个级数可以直接估值。对于通项的模是递减的级数,可以用艾肯特δ2过程加速收敛。对交错级数(和式中项的符号交替变化),欧拉变换是强大的工具。van Wijngaarden方法是欧拉变换的一个精巧的实现方式。
2. 连分式求值
思想:连分式可作为科学计算中求函数值的有效工具,连分式如下面的形式:
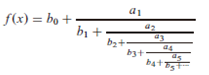
连分式通常比级数展开收敛要快得多,并且收敛区域更大。求解连分式的两个比较新的方法是Steed方法和改进的Lentz方法。连分式可以做一些等价变化来加速数值运算过程。连分式的奇部分和偶部分也是连分式,分别收敛到f2n和f2n+1。
3. 多项式和有理函数
略。。避免用最最直接的方法计算——p=c[0]+c[1]*x+c[2]*x*x+c[3]*x*x*x+c[4]*x*x*x*x;,而是用p=(((c[4]*x+c[3])*x+c[2])*x+c[1])*x+c[0]。
4. 复数运算
复数的加减法很简单,但乘除运算需要注意溢出。公式在书上。
5. 递推关系与Clenshaw递推公式
许多有用的函数满足递推关系,如勒让德多项式、第一类贝赛尔函数和指数积分以及三角函数。
Clenshaw递推公式是计算求和式的一种优秀而有效的方法,该和式是系数乘上遵循递推公式的函数之积。
6. 二次方程和三次方程
二次方程的2个根上过中学的应该都知道怎么求。。。三次的也不说了,google知道的。
7. 数值求导
利用导数的定义,函数值之差除以步长,几乎肯定得到的是不精确的结果。如非迫不得已不要考虑这种情况。
8. 切比雪夫逼近
n阶切比雪夫多项式用Tn(x)表示,写成公式为:Tn(x)=Dcos(n arccos x)。我们可以用切比雪夫多项式来逼近函数,然后用它的递推式来求解。
如果得到了某一范围内逼近一个函数的切比雪夫系数之后,把它们变换成与该函数微分和积分相对应的切比雪夫系数就很简单了。
(深入讨论略)
9. 线积分求函数值
有时候你会发现,对一个函数定义的微分方程直接积分,会得到效率更高的算法。
本文原创,转载请注明出处
http://www.cnblogs.com/luluathena/






的从设计到开发)


 记录)






)


