由投影重建图像

本由投影重建图像，主要是雷登变换与雷登把变换的应用，所以也没有太多的研究，只为了保持完整性，而添加到这里。

# 自制旋转投影图像# 模拟一个图像
img = np.zeros((100, 100))
img[45:46] = 0.25
img[46:47] = 0.5
img[47:48] = 0.75
img[48:51, :] = 1.
img[51:52, :] = 0.75
img[52:53, :] = 0.5
img[53:54, :] = 0.25total_img = img.copy()# 旋转并叠加, it's 32 on the book, but here I want to try 64, but degree / 2, see how is work, seems all the same
for i in range(64):    angle = (5.625) / 2 * (i + 1)C1 = cv2.getRotationMatrix2D((img.shape[1]/2.0, img.shape[0]/2.0), angle, 1)new_img = cv2.warpAffine(img, C1, (img.shape), borderValue=0)total_img = total_img + new_imgtotal_img = normalize(total_img)plt.figure(figsize=(13, 5))
plt.subplot(131), plt.imshow(img, 'gray'), plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(new_img, 'gray'), plt.title('new_img'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(total_img, 'gray'), plt.title('total_img'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()

投影和雷登变换 Johann Radon

$$g(\rho ,\theta )={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }f(x,y)\delta (x\theta +ysin\theta -\rho )dxdy$$

离散情况的雷登变换
$$g(\rho ,\theta )=\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y)\delta (x\theta +ysin\theta -\rho )$$

由雷登变换得到的图称之为正弦图(Sinogram)

from scipy import ndimagedef radon_transform(img, steps):"""radon tranform for gray imageparam: img: input Imageparam: steps: step for the transform, same of image height"""channels = img.shape[0]dst = np.zeros((channels, channels), dtype=np.float32)for i in range(steps):res = ndimage.rotate(img, -i * 180 / steps, reshape=False).astype(np.float32)dst[:, i] = sum(res)#     dst = ndimage.rotate(dst, 270, reshape=False) # 旋转后就跟书上的结果一致return dst

# 雷登变换
img_ori = cv2.imread("DIP_Figures/DIP3E_Original_Images_CH05/Fig0533(a)(circle).tif", 0)
m, n = img_ori.shape[1], img_ori.shape[0]
img = idea_low_pass_filter(img_ori, (m, n), D0=10)
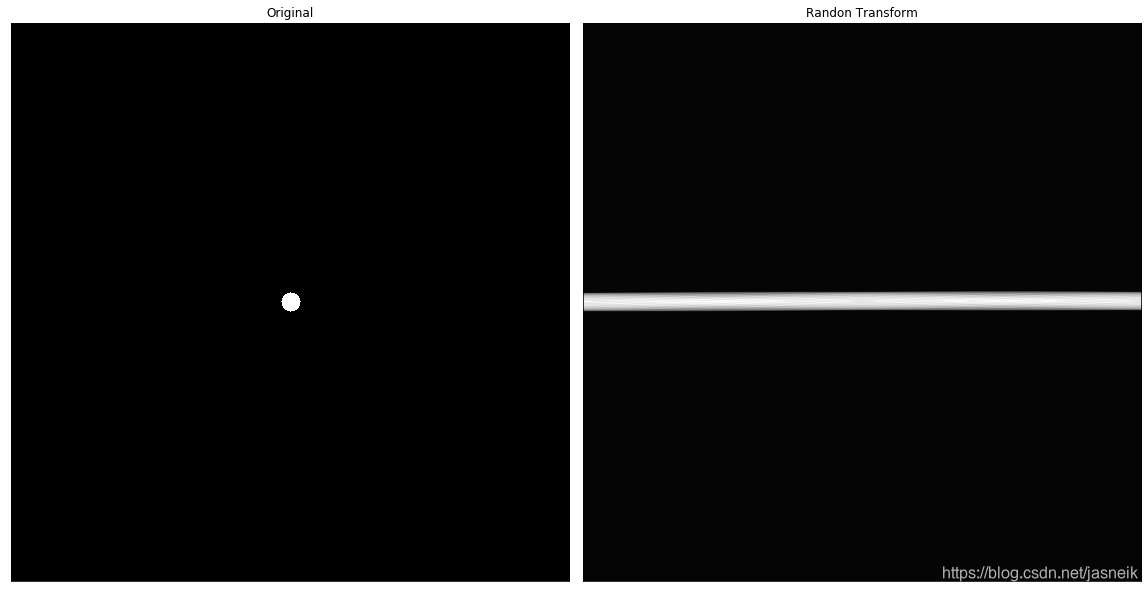
img_radon = radon_transform(img, img.shape[0])plt.figure(figsize=(24, 12))plt.subplot(131), plt.imshow(img, 'gray'), plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(img_radon, 'gray'), plt.title('Randon Transform'), plt.xticks([]), plt.yticks([])
# plt.subplot(133), plt.imshow(img_cv2_guass, 'gray'), plt.title('CV2 Guass')
plt.tight_layout()
plt.show()

# 两个物体的雷登变换
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH05/Fig0534(a)(ellipse_and_circle).tif', 0) #直接读为灰度图像
img_radon = radon_transform(img_ori, img_ori.shape[0])plt.figure(figsize=(24, 12))
plt.subplot(131), plt.imshow(img_ori, 'gray'), plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(img_radon, 'gray'), plt.title('Randon Transform'), plt.xticks([]), plt.yticks([])
# plt.subplot(133), plt.imshow(img_cv2_guass, 'gray'), plt.title('CV2 Guass')
plt.tight_layout()
plt.show()

# 长方形的雷登变换
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH05/Fig0539(a)(vertical_rectangle).tif', 0) #直接读为灰度图像img_radon = radon_transform(img_ori, img_ori.shape[0])plt.figure(figsize=(24, 12))plt.subplot(131), plt.imshow(img_ori, 'gray'), plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(img_radon, 'gray'), plt.title('Randon Transform'), plt.xticks([]), plt.yticks([])
# plt.subplot(133), plt.imshow(img_cv2_guass, 'gray'), plt.title('CV2 Guass')
plt.tight_layout()
plt.show()

# 多个物体雷登变换
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH05/Fig0539(c)(shepp-logan_phantom).tif', 0) #直接读为灰度图像img_radon = radon_transform(img_ori, img_ori.shape[0])plt.figure(figsize=(24, 12))plt.subplot(131), plt.imshow(img_ori, 'gray'), plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(img_radon, 'gray'), plt.title('Randon Transform'), plt.xticks([]), plt.yticks([])
# plt.subplot(133), plt.imshow(img_cv2_guass, 'gray'), plt.title('CV2 Guass')
plt.tight_layout()
plt.show()

反投影

$$f_{\theta }(x,y)=g(xcos\theta +ysin\theta ,\theta )$$
$$f(x,y)={\int }_0^{\pi }{f}_{\theta }(x,y)d\theta$$
$$f(x,y)=\sum _{\theta =0}^{\pi }{f}_{\theta }(x,y)$$

反投影的图像有时称为层图，我们可把层图理解为一幅由其生成投影的图像的一个近似。

from scipy import ndimagedef inverse_radon_transform(image, steps):"""inverse radon tranform for radon transform imageparam: image: input Imageparam: steps: step for the transform,  normaly same of image heightreturn: inverse radon transform for image, image is un-normalized"""channels = len(image[0])dst = np.zeros((steps, channels, channels))for i in range(steps):# 传入的图像中的每一列都对应于一个角度的投影值# 这里用的图像是上篇博文里得到的Radon变换后的图像裁剪后得到的temp = image[:, i]# 这里利用维度扩展和重复投影值数组来模拟反向均匀回抹过程temp_expand_dim = np.expand_dims(temp, axis=0)temp_repeat = temp_expand_dim.repeat(channels, axis=0)dst[i] = ndimage.rotate(temp_repeat, i*180 / steps, reshape=False).astype(np.float64)# 各个投影角度的投影值已经都保存在origin数组中，只需要将它们相加即可    iradon = np.sum(dst, axis=0)return iradon

# 雷登反变换
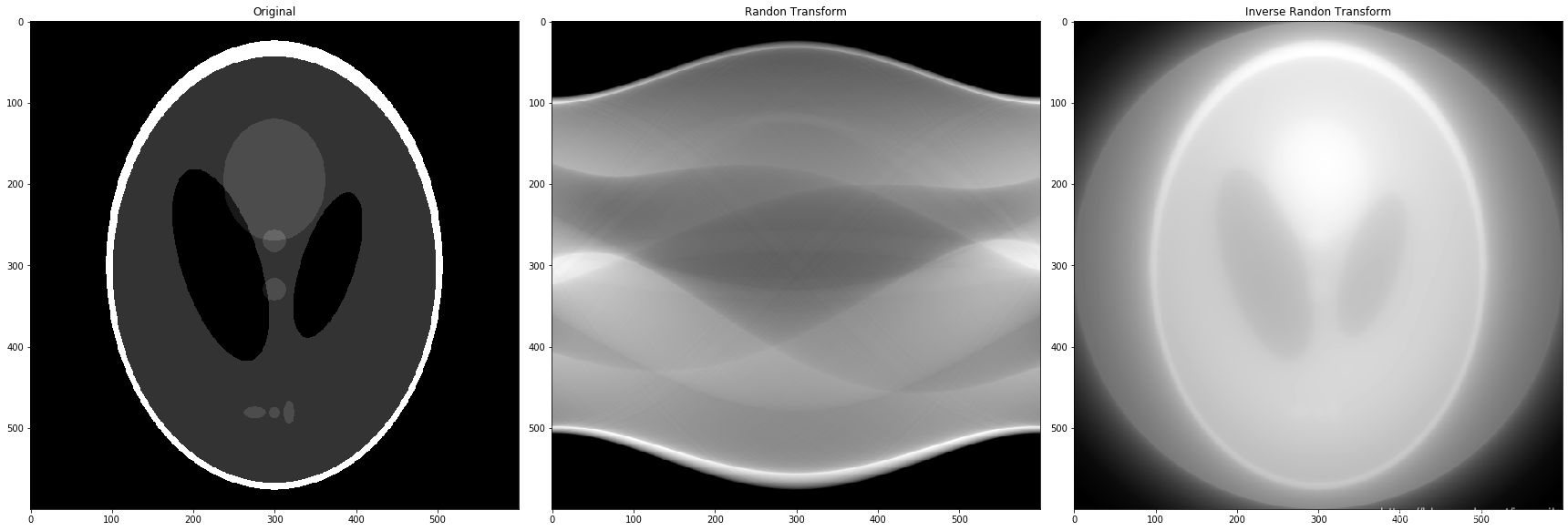
# img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH05/Fig0539(c)(shepp-logan_phantom).tif', 0) #直接读为灰度图像# img_radon = radon_transform(img_ori, img_ori.shape[0])img_inverse_radon = inverse_radon_transform(img_radon, img_radon.shape[0])plt.figure(figsize=(24, 12))plt.subplot(131), plt.imshow(img_ori, 'gray'), plt.title('Original')
plt.subplot(132), plt.imshow(img_radon, 'gray'), plt.title('Randon Transform')
plt.subplot(133), plt.imshow(img_inverse_radon, 'gray'), plt.title('Inverse Randon Transform')
plt.tight_layout()
plt.show()

# 两个物体的雷登反变换
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH05/Fig0534(a)(ellipse_and_circle).tif', 0) #直接读为灰度图像img_radon = radon_transform(img_ori, img_ori.shape[0])
img_inverse_radon = inverse_radon_transform(img_radon, img_radon.shape[0])plt.figure(figsize=(24, 12))
plt.subplot(131), plt.imshow(img_ori, 'gray'), plt.title('Original')
plt.subplot(132), plt.imshow(img_radon, 'gray'), plt.title('Randon Transform')
plt.subplot(133), plt.imshow(img_inverse_radon, 'gray'), plt.title('Inverse Randon Transform')
plt.tight_layout()
plt.show()

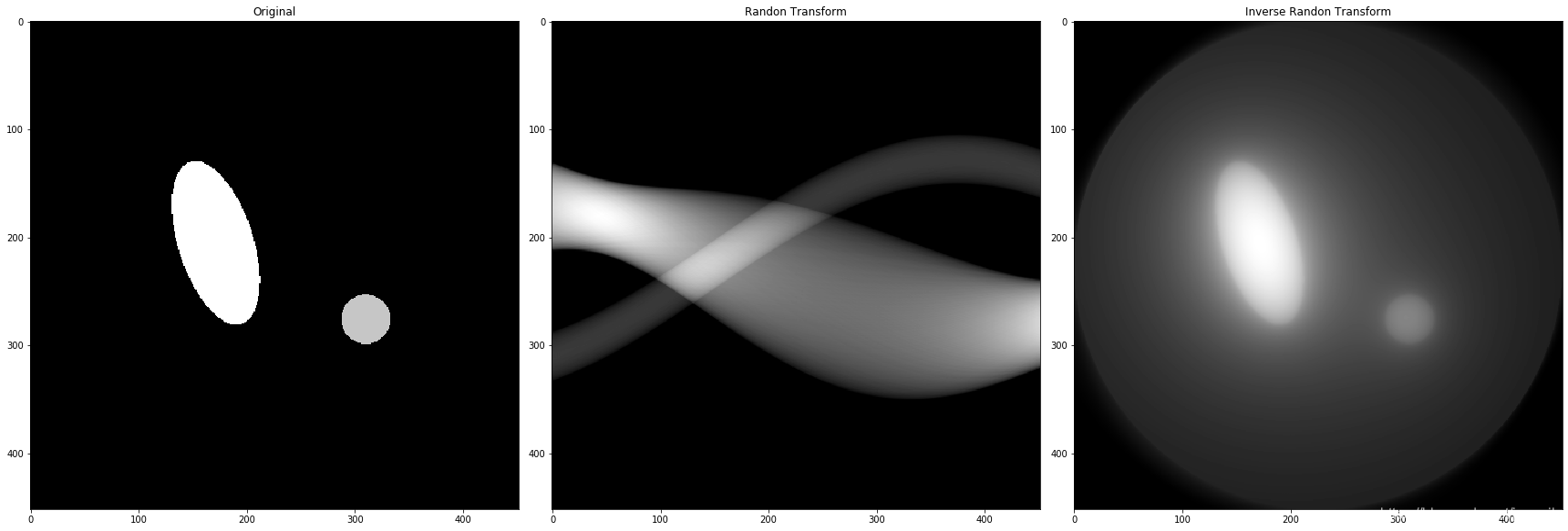
滤波反投影重建

$$f(x,y)={\int }_0^{\pi }{\int }_{-\infty }^{\infty }|\omega |G(\omega ,\theta )e^{j2\pi \omega (xcos\theta +ysin\theta )}d\omega d\theta$$

$$f(x,y)={\int }_0^{\pi }[{\int }_{-\infty }^{\infty }|\omega |G(\omega ,\theta )e^{j2\pi \omega \rho }d\omega {]}_{\rho =xcos\theta +ysin\theta }d\theta$$

$$h(\omega )=\{\begin{array}{ll}c+(c-1)cos\frac{2\pi \omega }{M},& 0\le \omega \le (M-1)\\ 0,& others\end{array}$$

当$c=0.54$时，该函数称为汉明窗(Richard Hamming)；当$c=0.5$时，该函数称为韩窗(Julius von Hann)。汉明窗和韩窗的主要区别是，韩窗末尾的一些点为零。通常两者的差别在图像处理应用中是觉察不到的。

反投影图像$f(x,y)$是按如下步骤得到的：

1. 计算每个投影的一维傅里叶变换。
2. 将每个全里叶变换乘以滤波器传弟函数$|\omega |$，这个传递函数已乘以一个合适的窗（如汉明窗）。
3. 得到的每个滤波后的变换的一维傅里叶反变换。
4. 对步骤3得到的所有一维反变换进行积分（求和）。

顾名思义，滤波反投影就是先对投影值进行滤波，然后利用的得到的值进行反投影，简单来说滤波的主要目的就是使边缘（对应于图像的高频部分）更加明显。理论上来说，滤波函数应该是：
$$h(\omega )=|\omega |$$

但是这个是一个理想滤波器，没办法实现，因此需要考虑其他能够实现并且能够使得到的图像更加接近原始图像的滤波器。这里我仅介绍两种R—L滤波器和S—L滤波器，下面是这两种滤波器的具体形式：
$$h_{RL}(n\delta )=\{\begin{array}{ll}-\frac{1}{4{\delta }^2},& n=0\\ 0,& n为偶数\\ -\frac{1}{(n\pi \delta {)}^2},& n为奇数\end{array}$$

$$h_{SL}=\frac{1}{{\pi }^2{\delta }^2(4n^2-1)}$$

利用以上两个滤波器和投影值进行卷积，然后再进行反投影，就可以得到得到原始的图像，大致上来说，就是在上面的代码中增加滤波器的构建和投影与滤波器的卷积过程，具体的代码如下：

def box_filter(M, c):hw = np.zeros((M, ))for w in range(M):if 0 <= w <= M - 1:hw[w] = c + (c - 1) * np.cos(2 * np.pi * w / M)else:hw[w] = 0hw = np.fft.fft(hw)hw = np.fft.fftshift(hw)hw = np.real(hw)
#     hw = normalize(np.real(hw))return hw

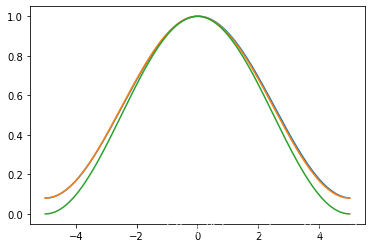
# 1维汉明窗
x = np.linspace(-5, 5, 200)M = x.shape[0]y = abs(x)c = 0.54hw = np.zeros_like(x)
for w in range(M):if 0 <= w <= M - 1:hw[w] = c + (c - 1) * np.cos(2 * np.pi * w / M)else:hw[w] = 0np_hamming = np.hamming(M)
np_hann= np.hanning(M)# plt.plot(x, y)
plt.plot(x, hw)
plt.plot(x, np_hamming)
plt.plot(x, np_hann)
plt.show()

def hamming_window(img, hamming=True):"""2d hamming and hann windowparam: img, input imageparam: hamming: bool, if True return hamming windows, if False return hann windowreturn normalize 2d hamming or hann windowProblem: I still not very sure if this right, since result is not very good."""M, N = img.shape[1], img.shape[0]if hamming:u = np.hamming(M)v = np.hamming(N)else:u = np.hanning(M)v = np.hanning(N)u, v = np.meshgrid(u, v)high_pass = np.sqrt(u**2 + v**2)#     high_pass = np.sqrt((u - M//2)**2 + (v - N//2)**2)kernel = high_pass # 1 / (1 + ((high_pass * W) / (high_pass ** 2 - D0 **2 + 1e-5))**(2*order))return kernel

# 二维汉明窗
img_hamming = hamming_window(img_radon, hamming=True)# img_radon_hamming = normalize(img_hamming * img_radon)
img_radon_hamming = img_hamming * img_radonplt.figure(figsize=(24, 12))plt.subplot(131), plt.imshow(img_radon, 'gray'), plt.title('img radon'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(img_hamming, 'gray'), plt.title('img_hamming'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(img_radon_hamming, 'gray'), plt.title('img_radon_hamming'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()

#两种滤波器的实现
def rl_filter(N, d):filterRL = np.zeros((N,))for i in range(N):filterRL[i] = - 1.0 / (np.power((i - N / 2) * np.pi * d, 2.0) + 1e-5) # 1e-5 加上一个不为零的小数，防止出现除0的问题if np.mod(i - N / 2, 2) == 0:filterRL[i] = 0filterRL[int(N/2)] = 1 / (4 * np.power(d, 2.0))return filterRLdef sl_filter(N, d):filterSL = np.zeros((N,))for i in range(N):filterSL[i] = - 2 / (np.pi**2.0 * d**2.0 * (4 * (i - N / 2)**2.0 - 1))return filterSLdef inverse_filter_radon_transform(image, steps):#定义用于存储重建后的图像的数组channels = len(image[0])origin = np.zeros((steps, channels, channels))
#     filter = box_filtechannelschannels, 0.48)
#     filter = rl_filter(channels, 1)filter = sl_filter(channels, 1)for i in range(steps):projectionValue = image[:, i]projectionValueFiltered = np.convolve(filter, projectionValue, "same")projectionValueExpandDim = np.expand_dims(projectionValueFiltered, axis=0)projectionValueRepeat = projectionValueExpandDim.repeat(channels, axis=0)origin[i] = ndimage.rotate(projectionValueRepeat, i*180/steps, reshape=False).astype(np.float64)iradon = np.sum(origin, axis=0)return iradon

# 两种滤波器的实现
hx = box_filter(200, 0.5)
sl = sl_filter(200, 1)plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1), plt.plot(x, hx)
plt.subplot(1, 2, 2), plt.plot(x, sl)
plt.show()

# 多个物体的反投影
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH05/Fig0539(c)(shepp-logan_phantom).tif', 0) #直接读为灰度图像img_radon = radon_transform(img_ori, img_ori.shape[0])
img_inverse_radon = inverse_radon_transform(img_radon, img_radon.shape[0])
img_filter_inverse_radon = inverse_filter_radon_transform(img_radon, img_radon.shape[0])plt.figure(figsize=(18, 6))plt.subplot(131), plt.imshow(img_ori, 'gray'), plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(img_inverse_radon, 'gray'), plt.title('Inverse Randon Transform'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(img_filter_inverse_radon, 'gray'), plt.title('Inverse Filter Randon Transform')
plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()

# 长方形的反投影
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH05/Fig0539(a)(vertical_rectangle).tif', 0) #直接读为灰度图像img_radon = radon_transform(img_ori, img_ori.shape[0])
img_inverse_radon = inverse_radon_transform(img_radon, img_radon.shape[0])
img_hamming = hamming_window(img_radon, hamming=True)
img_radon_hamming = img_hamming * img_radonimg_filter_inverse_radon = inverse_filter_radon_transform(img_radon_hamming, img_radon_hamming.shape[0])plt.figure(figsize=(18, 6))plt.subplot(131), plt.imshow(img_ori, 'gray'), plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(img_inverse_radon, 'gray'), plt.title('Inverse Randon Transform'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(img_filter_inverse_radon, 'gray'), plt.title('Inverse Filter Randon Transform')
plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()