
1、一元、多元函数导数与导数值计算
2、一元、多元函数高阶导数的计算
3、抽象复合函数的一阶、高阶导数计算
4、全微分的计算
5、方向导数的计算
工具:WolframAlpha计算搜索引擎
位置:http://www.wolframalpha.com,打开网页直接操作,其中windows app也可以通过Windows 10应用商店下载安装!
特别提示:如果使用网页版执行操作,不需要下载、安装任何软件,也不需要点任何链接,直接网页打开的那个搜索文本编辑框(如下图)输入表达式就可以了!系列推文中除特别强调外,显示的结果都能直接看到的!

手机:可以直接打开网页操作,或者自行网络搜索下载安装WolframAlpha APP版本操作
执行界面:网页、手机或平板等操作界面基本一致.
1、一元、多元函数一阶导数与导数值的计算
例1 计算以下函数的导数,并求在处的导数值:
输入表达式为
d/dx((x^3)cos(5x^2+e^(2x))-ln(3x^3-2x))执行后的结果如下图所示.
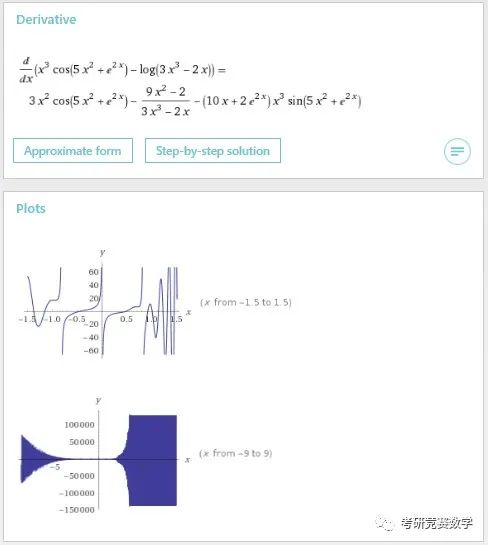
结果不仅显示导数结果,也给出了函数在不同范围内的图形. 输入表达式也可以直接以更自然的语言描述形式输入,比如输入:
derivative of (x^3)cos(5x^2+e^(2x))-ln(3x^3-2x)执行计算得到的结果一致.
在以上两种输入的表达式后面加上where x=1,比如输入
derivative of (x^3)cos(5x^2+e^(2x))-ln(3x^3-2x) where x=1执行计算后即得到导数值为
例2 计算以下函数的一阶偏导数和在处的偏导数值:
关于的偏导数计算输入表达式为
d/dx(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))执行后的结果为
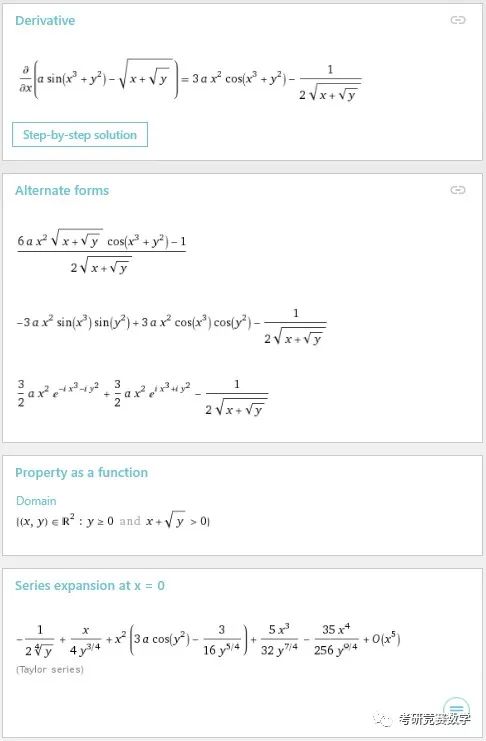
结果除了最上面给出导数结果之外,在下面还以不同的形式给出了导数结果描述. 另外给出了二元函数的定义域与关于变量的带皮亚诺余项的麦克劳林公式.
在以上表达式后面加上where (x,y)=(1,1),即可得该点处的偏导数值. 即输入
d/dx(a sin(x^3+y^2)-(x+y^(1/2))^(1/2)) where (x,y)=(1,1)执行计算后得到导数值为.
关于的偏导数计算输入表达式只要将以上输入表达式中的求导变量改为y就可以了. 即
d/dy(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))执行后的结果除了导数结果不同外,其余显示内容基本一致. 其中在处的一阶导数值为.
【注】 以上求导变量也可以指定为求导变量,比如输入
d/da(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))则计算结果为,即对变量求导,并显示导数结果图形.
2、一元、多元函数高阶导数的计算
例1 计算以下函数的50阶导数:
输入表达式为
d^50/dx^50((x^2)cosx)执行后的结果显示为
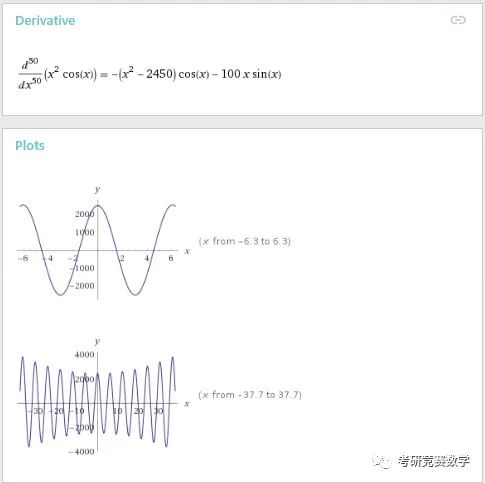
例2 求以下函数关于的三阶偏导数与关于的二阶偏导数的混合高阶偏导数:
输入表达式为
d^3/dx^3 d^2/dy^2 ((x^2+y^2)e^(x+y))执行后显示结果. 结果除了显示偏导数外,还会显示结果曲面图、等值线图,可能的其他表达形式以及方程的根分布情况,级数展开形式,不定积分及诶过与极小值点与极小值等信息,如下图.

3、抽象复合函数的一阶、高阶导数计算
将上面具体函数求导的函数表达式换成抽象函数即可.
例1 计算下列函数的一阶、二阶导数:
输入表达式为
d/dx (x^2)f(3x+4cosx), d^2/dx^2 (x^2)f(3x+4cosx)执行后的结果为

由于除了外还包含其他符号,所以结果以偏导数描述形式其输入形式.
例2 计算以下函数的导数:
输入表达式为
d^2/dx^2 f(x y, x^2-y^2), d/dx d/dy f(x y, x^2-y^2)执行后的结果为

4、全微分的计算
由于一元函数的微分就是导数乘以自变量微分
即完全可以直接归结为导数的计算,下面仅仅介绍多元函数全微分的计算方法.
例 计算以下函数的全微分:
直接输入表达式为
derivative of a sin(x^3+y^2)-(x+y^(1/2))^(1/2)自动识别变量为, ,执行计算后的结果不仅会得到全微分表达式,也会单独列出两个偏导数. 显示结果如下:
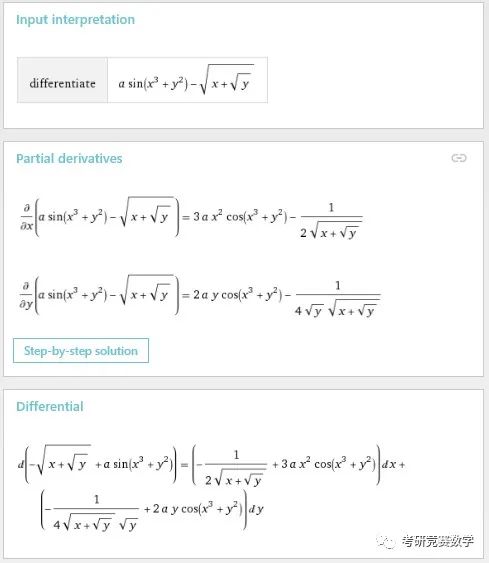
其中derivative可以替换为differential. 也可以直接基于Wolfram语言,也即Mathematica中的命令来执行计算,比如输入表达式
Dt(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))则将表达式中的符号都识别为变量符号,执行计算得到全微分表达式. 如下图.

只要令结果表达式中不是变量的符号,比如这里a它的微分令为0,即,得到的结果就是关于所有变量的微分表达式.
5、方向导数的计算
例1 计算以下函数指定方向的方向导数:
输入表达式为
derivative of x e^(2y)+cos(x y) in the direction (3,-4)执行后的结果显示为
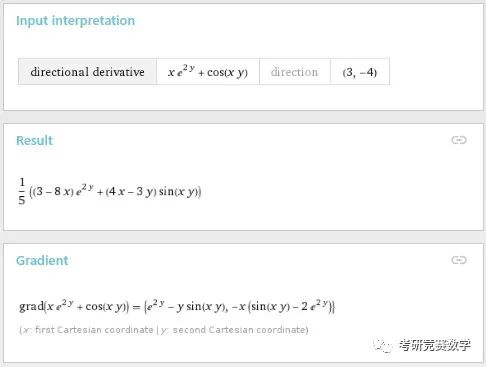
不仅给出了方向导数,也给出了函数的梯度向量.
例2 计算以下函数指定方向的方向导数:
输入表达式为
derivative of f(x,y) in the direction (a,b)执行后的结果显示为
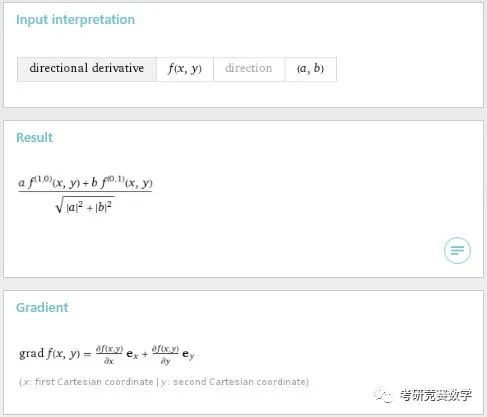
例3 计算以下函数指定方向和点处的方向导数:
输入表达式为
derivative 3x^2+2y^2+z^2 in direction (-2,-2,1) at point (1,2,3)执行后的结果显示为
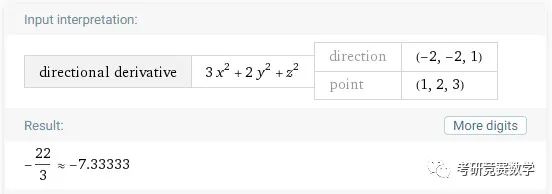
当然以上计算也可以直接依据求偏导数与方向导数计算公式,逐步计算代入得到结果.
微信公众号:考研竞赛数学(ID: xwmath)大学数学公共基础课程分享交流平台!支持咱号请点赞分享!

↓↓↓点查看更多相关内容


 JavaEE架构)

)














