本篇文章主要介绍三阶魔方总状态数是如何计算出来的,并介绍了两种算法,尽量保证语言通俗易懂,不涉及高深的理论知识(当然我也不懂:P)
一、4.33千亿亿到底有多大?
我们都知道三阶魔方的总变化状态数量为4.33千亿亿种,但是它具体是个多大的数字大家可能没有概念,因为据说超过1亿数量级的东西绝大多数人就没有数量上的概念了。

但我给大家做个简单的计算题就能理解了:
假设目前全国人口为14亿人,这14亿人每天24小时不停的转魔方,不吃不喝不睡觉,每人每秒钟可转出3种新的魔方状态,那么总共需要327年才能穷举出所有的魔方状态!
这327年足以让中国从康熙时期发展到新时代中国特色社会主义时期,让中国从闭关锁国走向改革开放,让……扯远了扯远了。
二、4.33千亿亿是如何算出来的?
1、先从分子说起:
三阶魔方相较于二阶和四阶(偶数阶)最主要的特点就是:有六个位置不变的中心块
这六个中心块构成了天然的X、Y、Z空间直角坐标系,把三阶魔方放到这个坐标系中,一个简单的魔方数学模型就建立起来了。
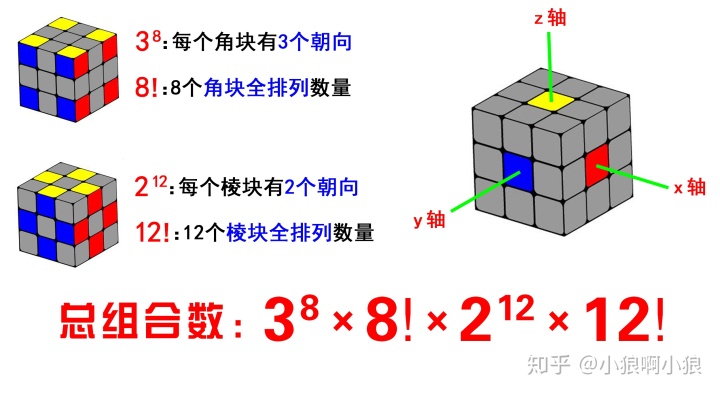
这个“总组合数”并非可还原的魔方的总状态数。它可以理解为把魔方拆了,再随机组装起来,一共可以得到的总组合数。它是正确值的12倍,下一小节将会解释“12”这个数字是怎么出现的。
2、再从公式的分母说起:
“2×3×2”是本文的关键所在
我们都知道并非所有的魔方随机组装好以后都能完全复原,也就是说总会出现一个棱块需要单独翻过来、一个角块需要单独转过来、两个棱块需要单独交换等等的错误情况
这些错误情况通过转动是永远不可能复原的。所以上面所谓的“总组合数”,其实是包含了这些组装错误的情况,将它们一并算在内所得到的结果。
下面就来看看一共有多少种随机组装情况:
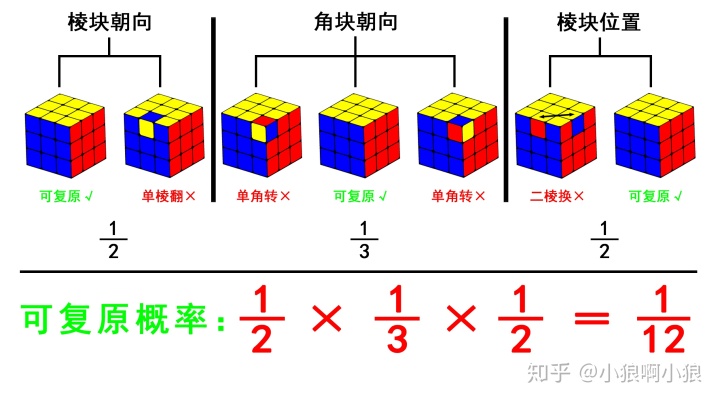
简单解释下这张图:
- 棱块的朝向只有2种,且无法单独翻转一个棱块
- 角块的朝向只有3种,且无法单独旋转一个角块
- 魔方是一个置换群,任意一步操作都是偶置换,只有偶置换的状态才能复原,所以无法单独交换一对棱块
学过盲拧的同学都能理解,也推荐看看魔方小站的这篇文章,做更深入的了解。或者你有更好的解释,欢迎在评论区留言。魔方小站魔方总变化数的道理www.rubik.com.cn

上图也就解释清楚了,为什么魔方随机组装之后能复原的概率只有
————————————————————
Q:可能有人会问,为什么只有棱块会出现只交换一对棱块的情况,角块不会出现只交换一对角块的情况吗?
A:这个问题很好,角块一样也会出现只交换一对角块的情况,但是学过PLL公式的同学都知道,角块和棱块交换情况是可以互相转换的(例如PLL邻角对棱换)。所以角块错误的情况可以转化为棱块的错误情况
三、另一种计算方法
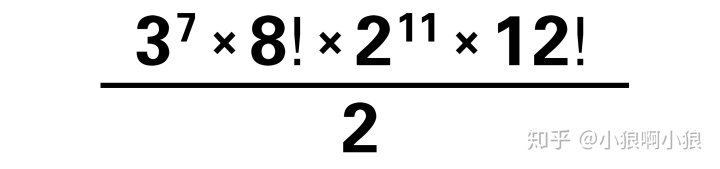
这种计算方法可以这么理解:
四、正N阶魔方的总状态数
(摘自百度百科)
欢迎转载~请务必标明出处!



















