第二章  线性规划（重点：单纯形法）

1.线性规划问题及其模型（重点：标准形式）

题型：是否为标准形式？不是的话化为标准形式！

1）问题的提出

提出问题：利率最大化???

确定决策变量>>>定义目标函数>>>确定约束条件>>>数学模型

2）基本概念

3）线性规划问题的共同特征：线性——最高次数为1

4）线性规划问题的一般形式与标准形式

①一般形式：><——表示可以大于也可以小于

②标准形式：三大特征——目标函数最小化、约束条件等式、决策变量非负

5）线性规划问题的标准化（按照标准形式三特征进行修改）

 

例1：非负松弛变量："<="变为"="——加上一个非负松弛变量使得等式可以成立

一般式：

标准化后：

 

例2：剩余变量：“>=”变为“=”——减去一个非负剩余变量（见例3）

 

例3：可正可负（无约束）变为“=”——用两个非负变量来代替那个无约束变量

2.线性规划求解基本原理

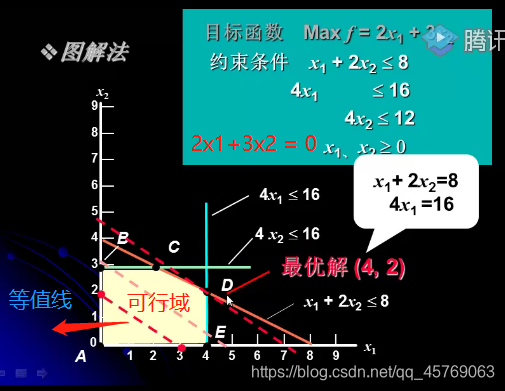
2.1 图解法（根据约束条件在坐标系中画出可行域，寻求最优解）

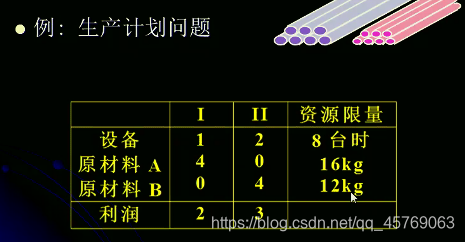
例1：

步骤：

1）可行域绘制

2）画目标函数的等值线（得到目标函数的斜率，一般令f=0）

3)移动等值线，往最优方向移动，直到不能移动

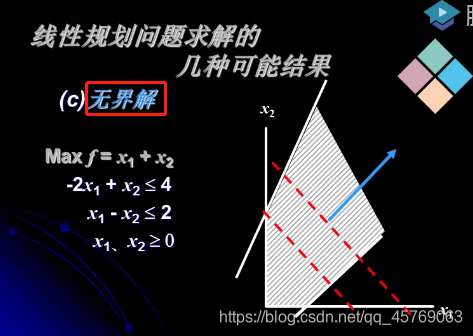
注：线性规划问题求解的几种可能结果

1）唯一解：只有一个解

2）无穷解：等值线与边界平行

3）无界解：可行域在最优的方向没有边界

4）无可行解：可行域为空集

 

2.2  线性规划问题解的概念

1. 可行解+最优解

正在上传…重新上传取消​

2.基：若B矩阵是A矩阵的非负子矩阵（|B|不等于0），则称B为A的一个基矩阵