文章目录
- 前言
- 一、点特征直方图
- 1.1 PFH
- 1.1.1 法线估计
- 1.1.2 特征计算
- 1.2 FPFH
- 1.3 VFH
- 二、示例
- 2.1 PFH计算
- 2.2 FPFH
- 2.3 VFH
前言
点特征直方图是PCL中非常重要的特征描述子,在点云匹配、分割、重建等任务中起到关键作用,可以对刚体变换、点云密度和噪声均有较强的抑制作用。而不同的描述子拥有不同优劣势,需要根据具体情况选择使用。
一、点特征直方图
点特征直方图融合了点云的局部和全局信息,具有旋转平移不变性,以及对采样密度和噪声点的稳健性。
1.1 PFH
PFH(point feature histogram)通过估计查询点和近邻点之间的法线差异,计算得到一个多维直方图来对点的K近邻进行几何描述,计算复杂度为O(nk^2)。
PFH的计算需要先估计法线,然后计算邻域范围内所有两点之间的关系:
1.1.1 法线估计
PCL采用近似估计的方法来计算法线特征,通过NormalEstimation类完成。
计算过程:
通过估计近邻区域的拟合面,再去计算查询点的法线。
拟合过程通过最小二乘法完成,然后通过PCA方法计算得到法向量(构建协方差矩阵,奇异值分解计算矩阵最小特征值所对应的特征向量做为法向量),最后通过计算相邻点法线内积的方法来进行法线定向。
实现过程可以参考:
为什么用PCA做点云法线估计?
源代码:
inline boolcomputePointNormal (const pcl::PointCloud<PointInT> &cloud, const std::vector<int> &indices,float &nx, float &ny, float &nz, float &curvature){//计算协方差矩阵if (indices.size () < 3 ||computeMeanAndCovarianceMatrix (cloud, indices, covariance_matrix_, xyz_centroid_) == 0){nx = ny = nz = curvature = std::numeric_limits<float>::quiet_NaN ();return false;}// Get the plane normal and surface curvaturesolvePlaneParameters (covariance_matrix_, nx, ny, nz, curvature);return true;}
计算法线和曲率,其中nx,ny,nz为法线的xyz分量。
inline void
solvePlaneParameters (const Eigen::Matrix3f &covariance_matrix,float &nx, float &ny, float &nz, float &curvature)
{// Avoid getting hung on Eigen's optimizers
// for (int i = 0; i < 9; ++i)
// if (!std::isfinite (covariance_matrix.coeff (i)))
// {
// //PCL_WARN ("[pcl::solvePlaneParameteres] Covariance matrix has NaN/Inf values!\n");
// nx = ny = nz = curvature = std::numeric_limits<float>::quiet_NaN ();
// return;
// }// Extract the smallest eigenvalue and its eigenvectorEIGEN_ALIGN16 Eigen::Vector3f::Scalar eigen_value;EIGEN_ALIGN16 Eigen::Vector3f eigen_vector;pcl::eigen33 (covariance_matrix, eigen_value, eigen_vector);nx = eigen_vector [0];ny = eigen_vector [1];nz = eigen_vector [2];// Compute the curvature surface changefloat eig_sum = covariance_matrix.coeff (0) + covariance_matrix.coeff (4) + covariance_matrix.coeff (8);if (eig_sum != 0)curvature = std::abs (eigen_value / eig_sum);elsecurvature = 0;
}
确定法线方向,vp_x,vp_y,vp_z为视点的坐标:
template <typename PointT> inline voidflipNormalTowardsViewpoint (const PointT &point, float vp_x, float vp_y, float vp_z,float &nx, float &ny, float &nz){// See if we need to flip any plane normalsvp_x -= point.x;vp_y -= point.y;vp_z -= point.z;// Dot product between the (viewpoint - point) and the plane normalfloat cos_theta = (vp_x * nx + vp_y * ny + vp_z * nz);// Flip the plane normalif (cos_theta < 0){nx *= -1;ny *= -1;nz *= -1;}}
1.1.2 特征计算

1:计算两点法线的差异角度。
2:计算查询点法线方向与两点连线方向的角度。
3:计算邻域点法线上一点到UW平面的垂线交点与邻域点的直线,再计算直线与U的角度值。
4:计算两点间的距离。

按以上公式,每两个查询点可以计算出4个特征值。PCL中忽略d特征,只保留3个角度特征。
特征的统计方式按照划分子区间,并统计每个子区间的点数目,同时将角度归一化到相同的区间。PCL将每个角度特征划分5个子区间进行统计,最终得到125个浮点元素的特征向量,可以保存在PFHSignature125类型中。
特征计算:
PCL_EXPORTS bool computePairFeatures (const Eigen::Vector4f &p1, const Eigen::Vector4f &n1, const Eigen::Vector4f &p2, const Eigen::Vector4f &n2, float &f1, float &f2, float &f3, float &f4);
直方图计算:
template <typename PointInT, typename PointNT, typename PointOutT> void
pcl::PFHEstimation<PointInT, PointNT, PointOutT>::computePointPFHSignature (const pcl::PointCloud<PointInT> &cloud, const pcl::PointCloud<PointNT> &normals,const std::vector<int> &indices, int nr_split, Eigen::VectorXf &pfh_histogram)
1.2 FPFH
FPFH(Fast Point Feature Histograms)意为快速点特征直方图,该算法对特征的计算进行了简化,并运用特征加权的方式得到最终的FPFH特征。该算法减少了时间复杂度,增加了实时性。
具体的计算方法:
1:计算查询点p邻域范围内的所有点对特征(只与查询点相连的点对),得到PFH中三个角度特征,命名为SPFH特征。
2:计算邻域内其他点的SPFH特征。
3:将邻域内其他所有的SPFH特征加权得到最终的FPFH特征,权重w是用邻域内点的距离来进行度量的。PCL中将三个特征值中的每个按照11个特征子空间进行统计,组合得到一个33个浮点元素的特征向量来表示FPFH特征。

1.3 VFH
为了使计算得到的特征保持尺度不变性和区分不同的位姿,故引入视点变量,计算得到视点特征直方图VFH特征。
其计算方法为:
1:扩展FPFH,使其利用整个点云来进行计算估计,以点云的中心点c与其他点之间的点对作为计算单元。
2: 添加视点方向与每个点估计法线间的统计信息,其做法是在特征计算时将视点变量直接融入法线角度计算中来。

具体可参考:
PCL 估计一点云的VFH特征
计算出的特征由三部分构成:
1:三个角度特征,每个分为45个子区间进行统计。
2:基于质心的点云形状描述子,分为45个子区间进行统计。
3:视角方向与点法线方向的角度差异,分为128个子区间进行统计。
二、示例
2.1 PFH计算
//读取点云pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_ptr(new pcl::PointCloud<pcl::PointXYZ>);pcl::PCDReader reader;reader.read("plant.pcd", *cloud_ptr);//计算法线pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> ne;ne.setInputCloud(cloud_ptr);pcl::search::KdTree<pcl::PointXYZ>::Ptr tree1(new pcl::search::KdTree<pcl::PointXYZ>());ne.setSearchMethod(tree1);pcl::PointCloud<pcl::Normal>::Ptr cloud_normals_ptr(new pcl::PointCloud<pcl::Normal>);pcl::PointCloud<pcl::Normal>& cloud_normals = *cloud_normals_ptr;ne.setRadiusSearch(0.01);ne.compute(cloud_normals);//计算pfh特征pcl::PFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::PFHSignature125> pfh;pfh.setInputCloud(cloud_ptr);pfh.setInputNormals(cloud_normals_ptr);pcl::search::KdTree<pcl::PointXYZ>::Ptr tree2(new pcl::search::KdTree<pcl::PointXYZ>());pfh.setSearchMethod(tree2);//输出pcl::PointCloud<pcl::PFHSignature125>::Ptr pfh_ptr(new pcl::PointCloud<pcl::PFHSignature125>());pfh.setRadiusSearch(0.03);pfh.compute(*pfh_ptr);//显示pcl::visualization::PCLPlotter plotter;plotter.addFeatureHistogram(*pfh_ptr, 200); plotter.plot();

2.2 FPFH
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);pcl::PCDReader reader;reader.read("plant.pcd", *cloud);//法向量计算pcl::NormalEstimationOMP<pcl::PointXYZ, pcl::Normal> n;//OMP加速n.setInputCloud(cloud);pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>());n.setSearchMethod(tree);n.setNumberOfThreads(4);n.setKSearch(30);pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);n.compute(*normals);//计算特征pcl::FPFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::FPFHSignature33> fpfh;fpfh.setInputCloud(cloud);fpfh.setInputNormals(normals);pcl::search::KdTree<pcl::PointXYZ>::Ptr tree2(new pcl::search::KdTree<pcl::PointXYZ>());fpfh.setSearchMethod(tree2);pcl::PointCloud<pcl::FPFHSignature33>::Ptr fpfh_fe(new pcl::PointCloud<pcl::FPFHSignature33>());//注意:此处使用的半径必须要大于估计表面法线时使用的半径fpfh.setRadiusSearch(0.03);fpfh.compute(*fpfh_fe);cout << "phf feature size : " << fpfh_fe->points.size() << endl;pcl::visualization::PCLPlotter plotter;plotter.addFeatureHistogram(*fpfh_fe, 200);plotter.plot();
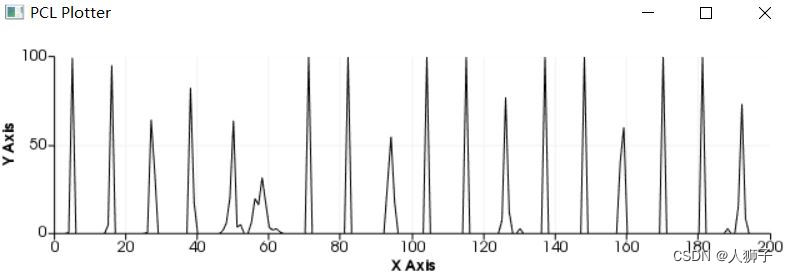
2.3 VFH
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);pcl::PCDReader reader;reader.read("plant.pcd", *cloud);pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> ne;pcl::search::KdTree<pcl::PointXYZ>::Ptr tree1(new pcl::search::KdTree<pcl::PointXYZ>());ne.setInputCloud(cloud);ne.setSearchMethod(tree1);ne.setRadiusSearch(0.01);pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);ne.compute(*normals);pcl::VFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::VFHSignature308> vfh;vfh.setInputCloud(cloud);vfh.setInputNormals(normals);pcl::search::KdTree<pcl::PointXYZ>::Ptr tree2(new pcl::search::KdTree<pcl::PointXYZ>());vfh.setSearchMethod(tree2);pcl::PointCloud<pcl::VFHSignature308>::Ptr vfh_ptr(new pcl::PointCloud<pcl::VFHSignature308>());vfh.compute(*vfh_ptr);pcl::visualization::PCLPlotter plotter;plotter.addFeatureHistogram(*vfh_ptr, 200);plotter.plot();

![BZOJ 1005: [HNOI2008]明明的烦恼](http://pic.xiahunao.cn/BZOJ 1005: [HNOI2008]明明的烦恼)






)








)

)
