本文参考的源码版本：gcc version 8.1.0 (x86_64-posix-seh-rev0, Built by MinGW-W64 project)。

priority_queue 本质是容器适配器，它对内部容器的元素有自己的管理方式，而 priority_queue 实际维护的是一个二叉堆。STL中 priority_queue 的操作是基于完全二叉树，使用随机访问迭代器访问元素，二叉堆在创建时按照层序遍历的顺序将数据放入容器中，因此创建 priority_queue 时使用的容器需要具有随机访问的特性。

priority_queue 是一个类模板，有三个模板参数，第一个数据的类型，第二个是容器的类型，默认为 vector ，第三个是用于比较操作的函数对象，默认是 less ，即小于比较。

template<typename _Tp, typename _Sequence = vector<_Tp>,typename _Compare  = less<typename _Sequence::value_type> >class priority_queue {};

完全二叉树

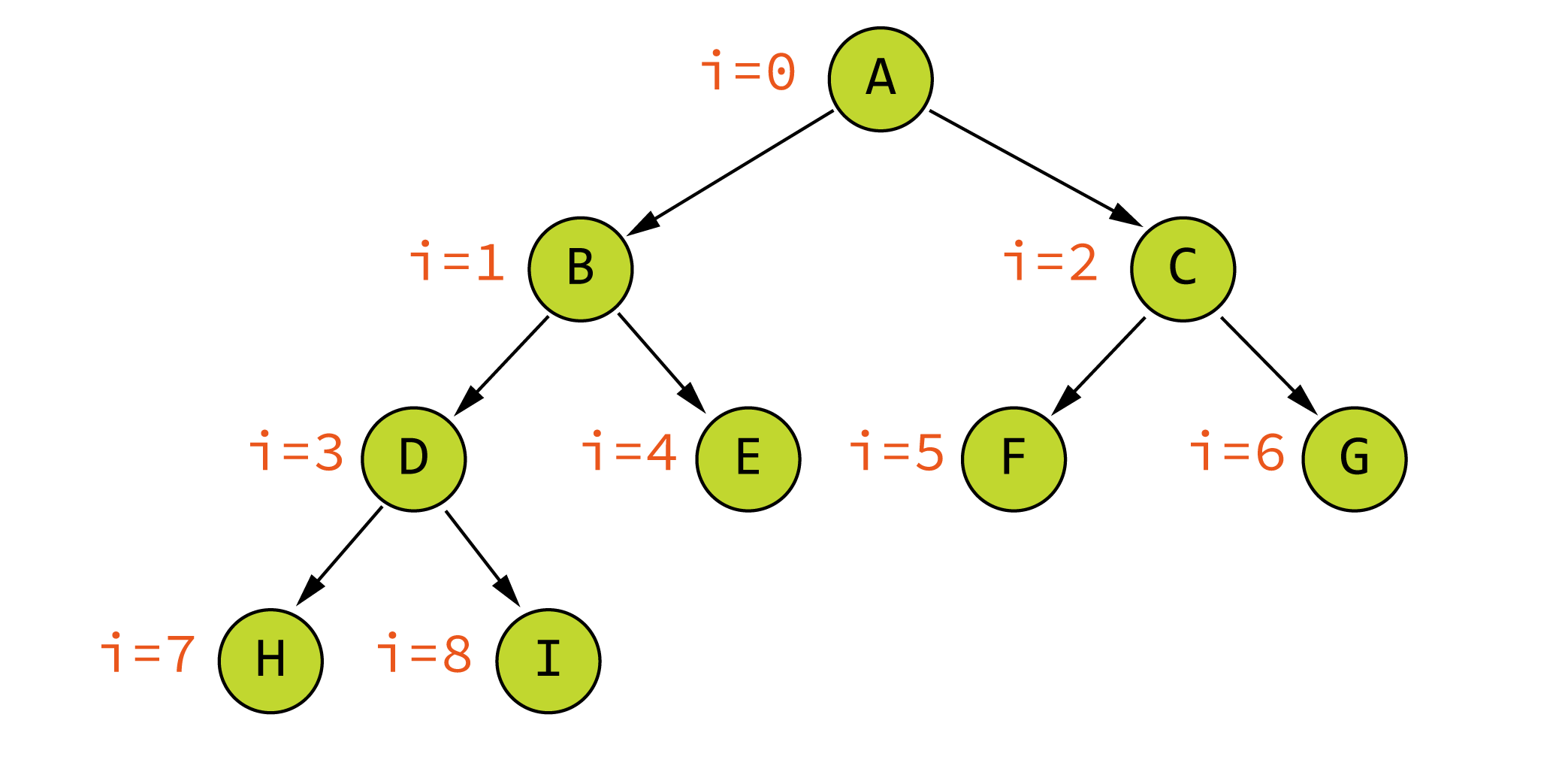
如果对满二叉树的结点进行编号, 约定编号从根结点起, 自上而下, 自左而右。则深度为 k 的, 有 n 个结点的二叉树, 当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应时, 称之为完全二叉树，换言之如果只删除了满二叉树最底层最右边的连续若干结点形成的树称为完全二叉树。满二叉树是完全二叉树的特列。完全二叉树具有以下特性：

• 具有 n 个节点的完全二叉树的深度为:

$$k=[lo{g}_{2}n{]}_{floor}+1$$

• 第 $i$ 个结点的编号范围为: $1\le i\le n$ ;
• 如果 $i=1$，$i$ 为根结点，无双亲；如果 $i>1$ ，结点$i$ 的双亲结点为：

$$[i/2{]}_{floor}$$

• 如果$2i<=n$ ，结点i的左孩子为结点 $2i$；否则无左孩子

• 如果 $2i+1<=n$，结点i的右孩子为结点 $2i+1$，否则无右孩子

• 结点 $i$ 所在的层次为:

  $$k_i=[lo{g}_{2}i{]}_{floor}+1$$

• 如果 $i>1$, $i$ 为奇数时，结点 $i$ 为右子结点； $i$ 为偶数时，结点 $i$ 为左子结点

STL的 priority_queue 在实现的时候保证了堆顶的元素始终位于容器的第一个位置，相当于二叉堆的完全二叉树的位置是从 0 开始计数，与完全二叉树的计数有细微差别。

堆有序化( reheapifying ) 中的上浮和下沉

当在二叉堆的最后一个位置插入新的元素时，新加入的元素可能会破坏堆的有序性，此时需要对新加结点与其父结点进行比较，如果大于父结点的值，那么就需要交换新加结点和父结点，如此重复比较，直到不再比父结点大时终止。这个过程就是堆有序化过程中的上浮操作。

当在移除二叉堆的堆顶元素时，被移除的元素破坏了堆的有序性，此时需要对堆顶的两个子结点中选择较大的值作为新的堆顶，而被选择的子结点则不能再作为子结点，则需继续比较其两个子结点，如此重复比较，直到到达堆底，或者两个子结点的值都比根结点小。这个过程就是堆有序化过程中的下沉操作。

#include <vector>
#include <random>
#include <chrono>using namespace std;class PriorityQueue {
public:void Push(int value) {v_.emplace_back(value);push_hole(v_.size() - 1,value);}void Pop() {int back = v_.back();int size = v_.size();int hole = 0;int right_child = 2 * (hole + 1); // 计算右孩子结点的位置while (right_child < size) {// 左孩子小于右孩子if (v_[right_child - 1] < v_[right_child]) {v_[hole] = v_[right_child];hole = right_child;} else { // 左孩子大于等于右孩子v_[hole] = v_[right_child - 1];hole = right_child - 1;}right_child = 2 * (hole + 1);}push_hole(hole, back);v_.pop_back(); // 最后才从容器中删除元素}int Top() const {return v_[0];};;int Empty() const {return v_.empty();}friend ostream &operator<<(ostream &os, const PriorityQueue &rhs) {for (const auto &v: rhs.v_) {os << v << " ";}os << endl;return os;}private:void push_hole(int hole,  int value) {int parent = (hole - 1) / 2; // 根据完全二叉树的特性计算父结点的位置// 父结点比新加的值小，交换父结点和新加入的值while (parent >= 0 && v_[parent] < value) {swap(v_[parent], v_[hole]);hole = parent;parent = (hole - 1) / 2;}v_[hole] = value;}private:vector<int> v_;
};int main() {PriorityQueue pq;default_random_engine  e(chrono::system_clock::now().time_since_epoch().count());uniform_int_distribution<int> d(1,1000);for (int i = 0; i < 100; i++) {pq.Push(d(e));}
//    vector<int> v{11,10,3,20,15,15,1,17,9,2,0,
//                  12,25,11,12,30,0,0,0,60,15,
//                  22,63,77,60,1,1,2,6,7,4,2,8};
//    for (int val : v) {
//        pq.Push(val);
//    }cout << "Container: " << pq;cout << "Top: ";while (!pq.Empty()) {int top = pq.Top();pq.Pop();cout << top << " ";}return 0;
}

priority_queue 的 push 操作

priority_queue 的 push 操作本质上就是二叉堆有序化的上浮，在真正的 push 前会先在容器的最后一个位置挖一个洞，以作为后续重排容器元素的中转位置。push 操作步骤如下：

1. 先将要添加的数据添加到容器最后一个位置，相当于挖个洞；
2. 然后对容器进行重排操作，重排操作的过程大致如下：
   • 初始时，洞的位置就是容器最后一个位置；
   • 如果容器本身是空的，那么在洞的位置添加新的元素后，该元素就堆顶的元素；
   • 如果容器本身不是空的，那么就通过洞的位置找到其父结点的位置，然后使用父结点的值与新加入的值进行比较，如果父结点的元素值小于新加入的值，那么就将父结点的值移到挖的洞中，这样中间位置就形成了一个洞，此时更新洞的位置。然后重复操作，直至洞的位置不再更新。
3. 将新加入的值添加到洞中，完成一次 push 操作。

示例：

下面是 push 重排的关键源码部分，第一个参数是容器的首元素迭代器，第二个参数是洞的初始位置，第三个参数是堆顶，即容器第一个位置，第四个参数是新添加的值，第五个参数是用于进行比较操作的函数对象。从源码能够看出，在比较操作的是时候，父结点作为了运算符的左侧运算对象，父结点比新加的结点小才会进行相应的操作，也就不难理解为什么 less 比较操作维护的却是大堆顶。

template<typename _RandomAccessIterator,typename _Distance, typename _Tp,typename _Compare>
void __push_heap(_RandomAccessIterator __first,_Distance __holeIndex,_Distance __topIndex,_Tp __value,_Compare& __comp) {_Distance __parent = (__holeIndex - 1) / 2; // 计算父结点索引// 比较父结点和要push的值大小关系while (__holeIndex > __topIndex && __comp(__first + __parent, __value)) {*(__first + __holeIndex) = _GLIBCXX_MOVE(*(__first + __parent));__holeIndex = __parent;__parent = (__holeIndex - 1) / 2;}// 将要push的值添加到洞里面*(__first + __holeIndex) = _GLIBCXX_MOVE(__value);}

priority_queue 的 pop 操作

priority_queue 的 push 操作本质上就是二叉堆有序化的下沉，pop 操作步骤如下：

1. 首先记录容器最后一个位置的元素值；
2. 将堆顶的元素移动到容器最后一个位置上，这样堆顶的位置就相当于形成了一个洞；
3. 然后调整堆，调整堆的过程大致如下：
   • 首先根据堆顶找到其右孩子结点，然后比较右孩子结点和左孩子结点的值，将两者中较大的值放置到堆顶;
   • 被移走的数值则形成了一个洞，因此需要继续向下比较，直到最后不再更新洞的位置
4. 将之前记录的最后一个位置的元素值 push 到最后一个孔的位置；
5. 最后从容器中移除最后一个位置的元素。

示例：

下面是 pop 调整堆的关键源码部分，第一个参数是容器的首元素迭代器，第二个参数是洞的初始位置，第三个参数是容器中除去要移除的元素后剩余的个数，第四个参数记录的pop前容器最后一个位置的元素，第五个参数是用于进行比较操作的函数对象。

template<typename _RandomAccessIterator, typename _Distance,typename _Tp, typename _Compare>
void __adjust_heap(_RandomAccessIterator __first,_Distance __holeIndex,_Distance __len,_Tp __value,_Compare __comp)
{const _Distance __topIndex = __holeIndex;_Distance __secondChild = __holeIndex;while (__secondChild < (__len - 1) / 2){// 计算某个父结点的右孩子结点索引__secondChild = 2 * (__secondChild + 1);// 比较左右两个孩子结点的大小，若左孩子结点大则更新索引if (__comp(__first + __secondChild,__first + (__secondChild - 1)))__secondChild--;*(__first + __holeIndex) = _GLIBCXX_MOVE(*(__first + __secondChild));__holeIndex = __secondChild;}// 剩余元素个数为偶数，说明完全二叉树的最后一个位置不是右孩子结点，就只能是左孩子结点// 而如果此时的洞是最后一个位置的父结点，那么就只能将左孩子结点的值移动到父结点处。if ((__len & 1) == 0 && __secondChild == (__len - 2) / 2){__secondChild = 2 * (__secondChild + 1);*(__first + __holeIndex) = _GLIBCXX_MOVE(*(__first+ (__secondChild - 1)));__holeIndex = __secondChild - 1;}__decltype(__gnu_cxx::__ops::__iter_comp_val(_GLIBCXX_MOVE(__comp)))__cmp(_GLIBCXX_MOVE(__comp));// 将之前记录的容器最后一个位置的值填入洞中std::__push_heap(__first, __holeIndex, __topIndex,_GLIBCXX_MOVE(__value), __cmp);
}

原文地址