目录

一、离散时间傅里叶变换DTFT

二、离散傅里叶变换DFT

三、DFT与DTFT的关系

​ 

---

参考：

《数字信号处理》——（一）.DTFT、DFT(python实现)_远行者223的博客-CSDN博客python绘制频谱图DTFT，DFTpython绘制频谱图：序列的傅里叶变换（DTFT），离散傅里叶变换（DFT）《数字信号处理》、python学习记录涉及知识（之前用matlab来画图，深感matlab打开、运行较慢，就学习了一下python，初学者，错误之处欢迎指正）DTFT原理；DFT原理；python matplotlib库DTFT、DFT原理一.DTFTX(ejω)=∑n=−∞∞x(n)e−jωnX\left(e^{j \omega}\right)=\sum_{n=-\https://blog.csdn.net/weixin_42193451/article/details/122384485

一、离散时间傅里叶变换DTFT

 

 时间序列变量范围（-∞，+∞）

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2022/3/20 17:56
# @Author  : @linlianqin
# @Site    : 
# @File    : DTFT.py
# @Software: PyCharm
# @description:https://blog.csdn.net/weixin_42193451/article/details/122384485import math
import numpy as np# 三角函数sin(nπ)的DTFTclass dtft():def __init__(self,xvalues:list):''':param xvalues: 时域自变量t序列'''self.yvalues = []self.xvalues = xvaluesdef xjw(self,fre:list):''':param fre: 频率自变量fre序列:return:'''# 实现yvalues为X（jw）频谱值## 遍历频率自变量for f in fre:p = 0# 遍历时间序列，得到累加和for x in self.xvalues:p = math.sin(x*np.pi)*math.e**(-1j*f*x) + pself.yvalues.append(p) # 对应每一个自变量频率的因变量值if __name__ == '__main__':import numpy as npfrom matplotlib import pyplot as pltxvalues = np.arange(-2,2,0.1)y1 = [np.sin(i*np.pi) for i in xvalues]# 原信号sin(nπ)plt.subplot(221)plt.plot(xvalues,y1)# 频谱DTFT = dtft(xvalues)freOmega = np.arange(0,20,0.01)DTFT.xjw(freOmega)plt.subplot(222)plt.plot(freOmega,DTFT.yvalues)# 幅度谱plt.subplot(223)plt.plot(freOmega,np.abs(DTFT.yvalues))# 相位谱plt.subplot(224)angle_ = np.angle(DTFT.yvalues)/np.piplt.plot(freOmega,180*angle_)plt.show()

 二、离散傅里叶变换DFT

 时间序列变量n为离散取值（0,N）,即0,1,2,3...,N

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2022/3/20 17:57
# @Author  : @linlianqin
# @Site    : 
# @File    : DFT.py
# @Software: PyCharm
# @description:https://blog.csdn.net/weixin_42193451/article/details/122384485import math
import numpy as npclass dft():def __init__(self,Num):''':param Num: dft点数,即离散取样点数'''super().__init__()self.Num = Numself.xk = [] # 存放dft计算结果self.K = list(range(0,self.Num,1)) # 时域序列横坐标，采样def Xk(self):# 计算频域中的频率自变量值W = []for x in self.K:W.append(x*2*math.pi/len(self.K))## 遍历频率自变量for f in W:p = 0# 遍历时间序列，得到累加和for k in self.K:p = math.sin(k*np.pi)*math.e**(-1j*f*k) + pself.xk.append(p) # 对应每一个自变量频率的因变量值if __name__ == '__main__':import numpy as npfrom matplotlib import pyplot as pltxvalues = np.arange(-2,2,0.1)y1 = [np.sin(i*np.pi) for i in xvalues]# 原信号sin(nπ)plt.subplot(221)plt.plot(xvalues,y1)# 频谱N = 16 # 采样点数DFT = dft(N)DFT.Xk()plt.subplot(222)plt.plot(DFT.K,DFT.xk)# 幅度谱plt.subplot(223)plt.stem(DFT.K,np.abs(DFT.xk))# 相位谱plt.subplot(224)angle_ = np.angle(DFT.xk)plt.stem(DFT.K,180*angle_/np.pi)plt.show()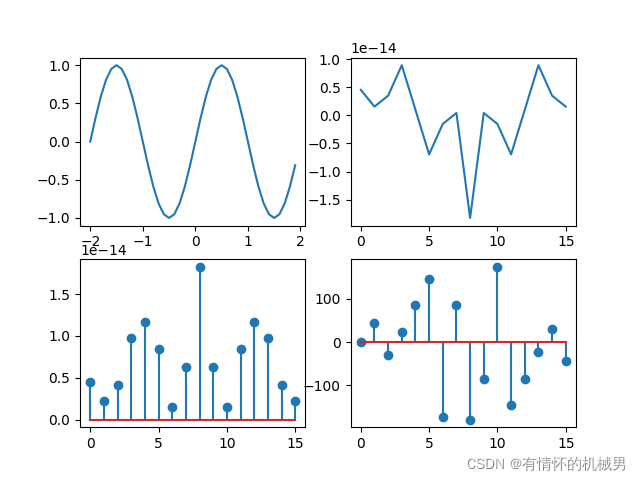

三、DFT与DTFT的关系

 

 DTFT.py

import math
import numpy as npclass dtft():
#xvalues:输入序列def __init__(self,xvalues=[]):self.yvalues = []self.xvalues = xvalues
#fre:频率坐标def xjw(self,fre = []):
#（式1-1）实现yvalues为X（jw）频谱值for f in fre:p = 0;for x in self.xvalues:p = math.e**(-1j*f*x) + pself.yvalues.append(p)

DFT.py

from DTFT import dtft
import mathclass dft(dtft):
#Num：dft点数，self.Num序列值，self.K 序列横坐标，self.xk：存放dft计算结果，
#self.Xk()：式（3-1）计算dftdef __init__(self,Num,xvalues):super().__init__(xvalues)self.Num = Numself.xk = []self.K = list(range(0,self.Num,1))self.Xk()def Xk(self):           W = []for x in self.K:W.append(x*2*math.pi/len(self.K))self.xjw(W)for x in self.yvalues:self.xk.append(abs(x))

使用方法和一、二一样，只是这里的DFT算法的编写是继承了DTFT类，便于理解二者的关系