椭圆基础知识
椭圆定义:椭圆上任意一点到两焦点的距离之和为2a
如何由椭圆定义推出椭圆标准方程呢?
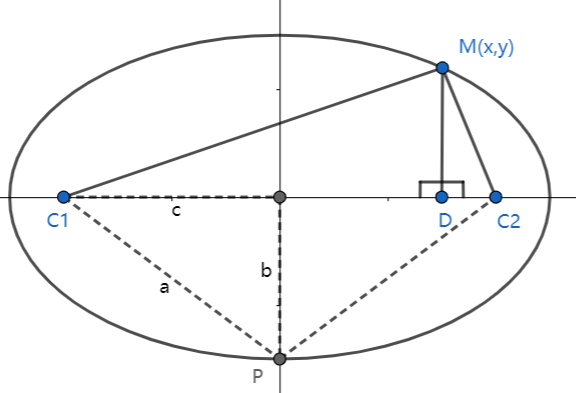
如上图所示。 由定义可得已知条件为 ∣ M C 1 ∣ + ∣ M C 2 ∣ = 2 a 当 M 落在顶点 P 上时,可得另一已知条件 a 2 − b 2 = c 2 当有了已知条件之后,可以通过 R T △ M C 1 D 和 M C 2 D 写出如下等式: ( x + c ) 2 + y 2 + ( x − c ) 2 + y 2 = 2 a 该式可通过两边平方消除根式,且化简过程中要用 a 2 − b 2 代替 c 2 该式化简有一定计算量,在此不写出详细步骤 但最终一定能化简为 x 2 a 2 + y 2 b 2 = 1 即有了定义之后,椭圆上任意一点 M 满足该方程 如上图所示。 \\ 由定义可得已知条件为|MC1|+|MC2|=2a \\ 当M落在顶点P上时,可得另一已知条件a^2-b^2=c^2 \\ 当有了已知条件之后,可以通过RT\triangle MC1D和MC2D写出如下等式: \\ \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2a \\ 该式可通过两边平方消除根式,且化简过程中要用a^2-b^2代替c^2 \\ 该式化简有一定计算量,在此不写出详细步骤 \\ 但最终一定能化简为\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\ 即有了定义之后,椭圆上任意一点M满足该方程 如上图所示。由定义可得已知条件为∣MC1∣+∣MC2∣=2a当M落在顶点P上时,可得另一已知条件a2−b2=c2当有了已知条件之后,可以通过RT△MC1D和MC2D写出如下等式:(x+c)2+y2+(x−c)2+y2=2a该式可通过两边平方消除根式,且化简过程中要用a2−b2代替c2该式化简有一定计算量,在此不写出详细步骤但最终一定能化简为a2x2+b2y2=1即有了定义之后,椭圆上任意一点M满足该方程
椭圆标准方程: 当焦点在 x 轴时, x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) 当焦点在 y 轴时, y 2 a 2 + x 2 b 2 = 1 ( a > b > 0 ) 焦距 c 与 a , b 的关系: a 2 − b 2 = c 2 椭圆面积公式: π a b ,当 a = b 时,即圆的面积公式 π a 2 椭圆标准方程:\\ 当焦点在x轴时,\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) \\ 当焦点在y轴时,\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(a>b>0) \\ \,\\ 焦距c与a,b的关系:a^2-b^2=c^2 \\ 椭圆面积公式:\pi ab,当a=b时,即圆的面积公式\pi a^2 椭圆标准方程:当焦点在x轴时,a2x2+b2y2=1(a>b>0)当焦点在y轴时,a2y2+b2x2=1(a>b>0)焦距c与a,b的关系:a2−b2=c2椭圆面积公式:πab,当a=b时,即圆的面积公式πa2
椭圆参数方程
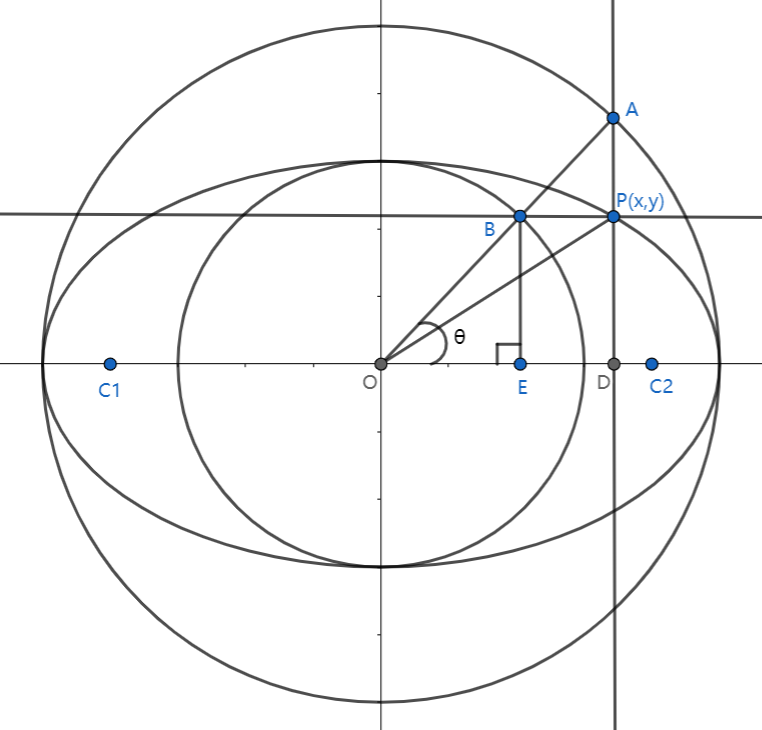
如上图所示。 分别作椭圆的外接圆和内接圆 容易得知两个圆方程分别为 x 2 + y 2 = a 2 , x 2 + y 2 = b 2 取大圆上一点 A (或小圆上一点 B ),连接 O A 与小圆相较于 B 过点 A 作一条垂直直线,过点 B 作一条水平直线,相交于 P 此时点 P ( x , y ) 在不在椭圆上并不知道,下面求出 x 和 y 的表达式 设 ∠ A O D = θ ,而 O A = a ,因此 x = a cos θ 在 △ B O E 中, O B = b ,因此 y = b sin θ 将 ( a cos θ , b sin θ ) 代入椭圆标准方程,等式成立 因此也就得到了椭圆的参数方程: { x = a cos θ y = b sin θ 这里的 θ 称为离心角,而 ∠ P O D 称为旋转角 由图可知离心角是由椭圆上一点和内接圆或外接圆确定的 如上图所示。\\ 分别作椭圆的外接圆和内接圆 \\ 容易得知两个圆方程分别为x^2+y^2=a^2,x^2+y^2=b^2 \\ 取大圆上一点A(或小圆上一点B),连接OA与小圆相较于B \\ 过点A作一条垂直直线,过点B作一条水平直线,相交于P \\ 此时点P(x,y)在不在椭圆上并不知道,下面求出x和y的表达式 \\ \,\\ 设\angle AOD=\theta,而OA=a,因此x=a\cos \theta \\ 在\triangle BOE中,OB=b,因此y=b\sin \theta \\ 将(a\cos \theta,b\sin \theta)代入椭圆标准方程,等式成立 \\ 因此也就得到了椭圆的参数方程: \begin{cases}x=a\cos \theta \\ y=b\sin \theta \end{cases} \\ 这里的\theta称为离心角,而\angle POD称为旋转角 \\ 由图可知离心角是由椭圆上一点和内接圆或外接圆确定的 如上图所示。分别作椭圆的外接圆和内接圆容易得知两个圆方程分别为x2+y2=a2,x2+y2=b2取大圆上一点A(或小圆上一点B),连接OA与小圆相较于B过点A作一条垂直直线,过点B作一条水平直线,相交于P此时点P(x,y)在不在椭圆上并不知道,下面求出x和y的表达式设∠AOD=θ,而OA=a,因此x=acosθ在△BOE中,OB=b,因此y=bsinθ将(acosθ,bsinθ)代入椭圆标准方程,等式成立因此也就得到了椭圆的参数方程:{x=acosθy=bsinθ这里的θ称为离心角,而∠POD称为旋转角由图可知离心角是由椭圆上一点和内接圆或外接圆确定的










canny边缘检测+仿射变换+透射变换)








