- 概述
在SLAM中,机器人位姿和地图都是状态变量,我们需要同时对这两个状态变量进行估计,即机器人获得一张环境地图的同时确定自己相对于该地图的位置。我们用x表示机器人状态,m表示环境地图,z表示传感器观测情况,u表示输入控制,下标表示时刻,则对
进行估计。而由条件贝叶斯法则,可以得到
这一分解相当于把SLAM分离为定位和构建地图两步,大大降低的SLAM问题的复杂度。基于此,Gmaping算法的大致过程为用上一时刻的地图和运动模型预测当前时刻的位姿,然后根据传感器观测值计算权重,重采样,更新粒子的地图,如此往复。ROS中实现的Gmapping算法框架大致如下,后面讲述原理时将说明对应的代码模块:

- 定位
Gmapping算法基于粒子滤波,因此定位部分和粒子滤波大致相同:粒子状态预测,测量,更新,重采样。接下来分别说明:
1、状态预测(draw from motion)
当前时刻粒子的状态首先由运动模型进行更新,在初始值上增加高斯采样的噪声,进行一个粗略状态估计。

在Gmapping算法中,则采用以下算法对运动进行采样:

2、测量(scan match)
这一步是在粗略估计的基础上做一次扫描匹配,找到一个使当前观测最贴合地图的位姿,以改进基于里程计模型的提议分布。基本思路是在基于运动模型预测的位姿,向负x,正x,负y,正y,左旋转,右旋转一共六个状态移动预测位姿,计算每个状态下的匹配得分,选择最高得分对应的位姿为最优位姿。
扫描匹配的重点就在于如何计算匹配得分。所谓匹配,是将当前采集的激光数据与环境地图进行对准:1)激光点的坐标转换至网格地图坐标;2)分别处理六个状态:当确定激光点网格坐标的地图值为障碍物时,进行打分(原理与NDT类似,距离越小,分数越大);3)得分最高的位姿为最优位姿。

获得最优粒子位姿后,可以把粒子采样范围从又扁又宽的区域更改到激光雷达观测模型所代表的尖峰区域L,新的粒子分布就可以更贴近于真实分布。

扫描匹配之后,我们就找到了L所代表的尖峰区域,接下来的任务是确定
该尖峰区域所代表的高斯分布的均值和方差。作者的方法是,在L中随机采样K个点,根据这K个点的里程计和观测模型计算均值和方差,如下式所示。

3、计算权重
然后,对于每个粒子,我们需要计算它的权重,以供后续的重采样步骤使用。由于在前面我们利用激光数据对提议分布进行了优化:

那么粒子的权重公式变成了:

这里还有一个问题就是权重计算,权重描述的是目标分布和提议分布之间的差别。因此我们在计算权重时就是计算我们模拟出的提议分布和目标分布的不同。而这种不同体现在我们是由有限的采样模拟出目标分布,因此权重的计算公式为:

4、重采样(update Tree Weights)
在执行重采样之前计算了每个粒子的权重,有时会因为环境相似度高或是由于测量噪声的影响会使接近正确状态的粒子数权重较小而错误状态的粒子的权重反而会大。重采样是依据粒子权重来重新采粒子的,这样正确的粒子就很有可能会被丢弃,频繁的重采样更加剧了正确但权重较小粒子被丢弃的可能性。
Gmapping算法中,作者采用权重值离差的量度进行重采样的判定。
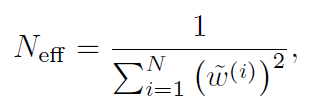
Neff越大,粒子权重差距越小。想象极端情况,当所有粒子权重都一样的时候(比如重采样之后),这些粒子恰好可以表示真实分布(类似于按照某个分布随机采样的结果)。当Neff降低到某个阈值以下,说明粒子的分布与真实分布差距很大,在粒子层面表现为某些粒子离真实值很近,而很多粒子离真实值较远,这时候恰好进行重采样。
- 建图
Gmapping算法会构建一个栅格地图,对二维环境进行了栅格尺度划分,而假设每一个栅格的状态是独立的。
对于环境中的一个点,我们用![]() 来表示它是Free状态的概率,用
来表示它是Free状态的概率,用![]() 来表示它是Occupied状态的概率,当然两者的和为1。为了更方便的表示,我们用
来表示它是Occupied状态的概率,当然两者的和为1。为了更方便的表示,我们用![]() 作为该点的状态,比值越大说明该点约可能是障碍物。
作为该点的状态,比值越大说明该点约可能是障碍物。
对于一个点,对于一个点,新来了一个测量值z之后我们需要更新它的状态。假设测量值来之前,该点的状态为![]() ,我们要更新它为:
,我们要更新它为:
![]() 。
。
由贝叶斯公式计算可得:

为了方便计算,我们对两边取对数:
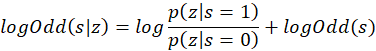
在没有任何测量值的初始状态下,一个点的初始状态为0,而这一部分关键的地方在于![]() 的计算,我们称这个比值为测量值的模型,标记为lomeas。实际上测量值的模型只有两种:
的计算,我们称这个比值为测量值的模型,标记为lomeas。实际上测量值的模型只有两种:![]() 和
和![]() ,而且都是定值。这样每获得一次测量值,我们都能用加减法对点状态进行更新。从而完成更新地图的工作。以下图为例:
,而且都是定值。这样每获得一次测量值,我们都能用加减法对点状态进行更新。从而完成更新地图的工作。以下图为例:

x是真实世界中的坐标,![]() 为栅格地图中的坐标,r为一格的长度,1/r表示分辨率,则
为栅格地图中的坐标,r为一格的长度,1/r表示分辨率,则![]() 。则二维情况下:
。则二维情况下:![]() 。假设图中机器人的位姿为(x,y,
。假设图中机器人的位姿为(x,y,![]() ),我们可以很容易计算障碍物的位置:
),我们可以很容易计算障碍物的位置:
![]()
其中,d为测量得到的距离,![]() 为激光线与机器人位姿角的夹角。我们得到两个坐标后能计算出两点在栅格地图的位置(i,j )与(
为激光线与机器人位姿角的夹角。我们得到两个坐标后能计算出两点在栅格地图的位置(i,j )与(![]() )。
)。
然后,我们利用bresenham算法(compute active area)来计算非障碍物格点的集合。然后利用上文所述结论,更新栅格地图即可。

Bresenham算法基本思想是采用递推步进的办法,令每次最大变化方向的坐标步进一个像素,同时另一个方向的坐标依据误差判别式的符号来决定是否也要步进一个像素。举例说明:

由于显示直线的象素点只能取整数值坐标,可以假设直线上第i个像素点坐标为(xi,yi),它是直线上点(xi,yi)的最佳近似,并且xi=xi(假设直线斜率小于1)。那么,直线上下一个像素点的可能位置是(xi+1,yi)或(xi+1,yi+1)。由图中可以知道,在x=xi+1处,直线上点的y值是y=m(xi+1)+b,该点离像素点(xi+1,yi)和像素点(xi+1,yi+1)的距离分别是d1和d2:
![]()
![]()
这两个距离差是
![]()
分析d1-d2,有以下三种情况:
- 当此值为正时,d1>d2,说明直线上理论点离(xi+1,yi+1) 像素较近,下一个像素点应取(xi+1,yi+1)。
- 当此值为负时,d1<d2,说明直线上理论点离(xi+1,yi) 像素较近,则下一个像素点应取(xi+1,yi)。
- 当此值为零时,说明直线上理论点离上、下两个像素点的距离相等,取哪个点都行,算法规定这种情况下取(xi+1,yi+1)作为下一个像素点。
因此只要利用(d1-d2)的符号就可以决定下一个像素点的选择。
参考文献
- https://blog.csdn.net/qq_36355662/article/details/90301219
- https://blog.csdn.net/shixiaolu63/article/details/93739379
- https://www.jianshu.com/p/f044da681454
- https://blog.csdn.net/liuyanpeng12333/article/details/81946841
- https://www.cnblogs.com/yhlx125/p/5634128.html
- 概率机器人
- 粒子滤波:从推导到应用
- Improved Techniques for Grid Mapping with Rao-Blackwellized Particle Filters
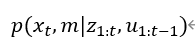









![[TOOLS] 移动端调试进行时 - whistle](http://pic.xiahunao.cn/[TOOLS] 移动端调试进行时 - whistle)




)




