众所周知，二维码通常是黑白的，而且是由若干个长方形或正方形小块平铺而成。但从人们的审美角度来看，常见的黑白二维码不免让人审美疲劳。本文试着从分块上色的角度对二维码进行美化，并尝试讲一下“美化”的编程思路。

一、缘由及目的：

首先，我们来看看正常情况下的黑白二维码，如图1：

图1  普通二维码（黑白条块）

上色的难点在于如何上色，上什么色，也就是哪些块“着”什么颜色。（关于彩色二维码的效果，请参考我的另一篇文章：《C#彩色艺术化二维码样式设计（仅说思路）》http://blog.csdn.net/johnsuna/article/details/7933619）

如果上错了色，也会成为“大花脸”，变得并不艺术。就好像漂亮的农村姑娘，如果穿上大花衣裳，看上去鲜艳，但仍然显示不出其天生的丽质，反而显得“很土”。如下图2及图3：

 

图2   大花脸式的彩色二维码

图3  单块随机色（彩色）二维码

而上色的难点在于分块，也就是将二维码分成多少块、如何分块，相关色块上什么颜色，后一个问题是美术工程师考虑的，不在本文讨论范围之内。从图1，图2来看，分块的归类并不容易或者说我们从外观上还不好判断哪些块分在一起成为一个大色块。

经过上面图3、下面图4的圆角化处理后，色块的划分是显而易见的。具体如何圆角化处理，请见我的另一篇文章《C#彩色艺术化二维码样式设计（仅说思路）》http://blog.csdn.net/johnsuna/article/details/7933619 及http://blog.csdn.net/johnsuna/article/details/7948907。

图4  圆角化艺术二维码（黑白色）

为了阐述方便，我将图1的关键块进行了编号，如下图5所示：

图5   对图1黑白二维码相关关键色块进行编号

与图5相对应，图6为圆角化分块后的带编号的图片：

图6   对图2的关键块进行编号

下图7为们我要的最终效果：

图7  最终需要的效果示意

尽管我的上色功夫（美感）不怎么样，但总体效果比图1-图4的效果确实好多了。

二、算法研究：

如下图8所示，为了方便讲述，我将图7中色块7、8、9、10、11中的每个单元格又按a,b,c……进行了编号并给每个单元格加了一个黑边框。

图8  单元格

图8中，单元格7a和7b最终组成一个竖条色块，单元格8为一个独立的色块，9a与9b组成一个横条色块，而10a,10b...f 又组成一个L形的色块。如图7所示，12-18等由多个单元格彼此相连而组成一个大的色块，其中，编号为16的色块面积最大。

接下来，重点研究算法。

首先必须找到分块的“点”，观察图7和图8，我们经过对比可以发现，分隔各块之间的交接点有一个共同的规律：交接点外围相邻对角均为空。

具体地说，就是：以“交接点”为中心的3*3个单元格区域（含交接点本身）内，如果该交接点的外围8个点中，有两个斜角（不管是呈现“/”或“\”，也不管是哪一个角位，如左上或右下，或左下或右上）的点均为空白，那么，此点必为分块关键点，也就是“交接点”。

经过观察和研究，还有一种办法，那就是“广度优先遍历”。如下图：

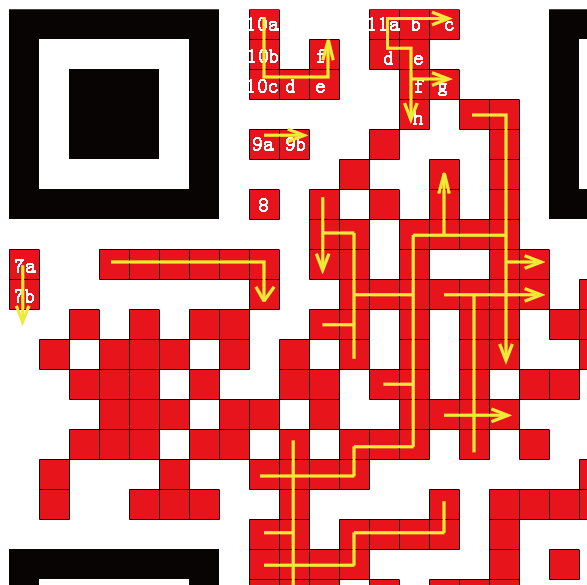
图9  单点水平/垂直延伸法示意

此算法也是棋牌或连连看等游戏常用的算法了。网上有很多类似的例子，就不再详解。另外，此算法可以与分形递归算法相结合，实现快速有效地对整个图像的分块上色。