在上一篇文章（https://blog.csdn.net/weixin_38636815/article/details/109495227）中我写了如何使用ceres，根据一系列的点来拟合一个平面，很难保证ORB-SLAM输出的轨迹严格与某一个坐标平面平行，所以这篇文章我我将说一下，如何将不与任何一个

坐标平面平行的三维平面绕着一个轴，旋转一个角度，使得其与某一个坐标平面平行。

一、原理分析

实现步骤：

1. 获得拟合出的平面的法向量

2. 找到参考向量，如要与XOY平面平行，参考向量为(0,0,1)的转置，与XOZ平面平行，参考向量为(0,1,0)的转置，与YOZ平面平行，参考向量为(1, 0, 0)的转置。

因为SLAM中的相机坐标系为（水平朝前放置相机时）Z轴朝前，X轴朝右， Y轴朝下，也就是说Z轴就是相机朝着的方向，我们在实际安装时也多数水平朝前安装

有时会有一些俯仰角，所以一般情况下我会把XOZ平面作为参考面，那么参考向量就是(0,1,0)向量的转置。

3. 根据“向量的点积”来求解两个向量之间的夹角。

 

4. 根据“向量的叉乘”求解垂直于两个向量构成的平面的法向量。因为两个向量的叉乘得到的新向量

就是一个同时垂直于两个向量的向量。

上面第4步求解出的向量就是我们的旋转轴，第三步求解出来的角度就是需要旋转的角度，我们将拟合出来的

平面绕着这个轴，旋转一个角度，就可以将这个平面旋转到与参考平面平行的地方。

注意：(1)上面求解出的角度是以弧度为单位，(2)上面求解出的旋转轴向量要进行归一化处理，否则后续求解的结果会出错。

二、代码讲解

下面有两种方法可以进行求解，一种是使用opencv的方法，一种是使用Eigen的方法。

1. 首先求解出旋转轴和旋转向量

//a,b,c为求解出的拟合平面的法向量，是进行归一化处理之后的向量。
cv::Point3d plane_norm(a, b, c);
//xz_norm是参考向量，也就是XOZ坐标平面的法向量
cv::Point3d xz_norm(0.0, 1.0, 0.0);
std::cout<<"plane_norm: "<<plane_norm<<std::endl;
std::cout<<"xz_norm: "<<xz_norm<<std::endl;
//求解两个向量的点乘
double v1v2 = plane_norm.dot(xz_norm);
//计算平面法向量和参考向量的模长，因为两个向量都是归一化之后的，所以这里的结果都是1.
double v1_norm = plane_norm.x*plane_norm.x + plane_norm.y*plane_norm.y + plane_norm.z*plane_norm.z;
double v2_norm = xz_norm.x*xz_norm.x + xz_norm.y*xz_norm.y + xz_norm.z*xz_norm.z;
//计算两个向量的夹角
double theta  = std::acos(v1v2/(std::sqrt(v1_norm)*std::sqrt(v2_norm)));//根据向量的叉乘求解同时垂直于两个向量的法向量。
cv::Point3d axis_v1v2 = xz_norm.cross(plane_norm);//对旋转向量进行归一化处理
double v1v2_2 = axis_v1v2.x*axis_v1v2.x + axis_v1v2.y*axis_v1v2.y + axis_v1v2.z*axis_v1v2.z;
double v1v2_n = std::sqrt(v1v2_2);
axis_v1v2 = axis_v1v2/v1v2_n;
std::cout<<"axis_v1v2: "<<axis_v1v2<<std::endl;
std::cout<<"theta: "<<theta<<std::endl;

2. 根据旋转轴和旋转向量求解旋转矩阵

（opencv法）

//-theta表示改变旋转的方向
cv::Point3d axis_v1v2_cv = -theta* axis_v1v2;//轴角，角度乘以方向
std::cout<<"axis_v1v2_cv: "<<axis_v1v2_cv<<std::endl;cv::Mat R_vec=(cv::Mat_<double>(3,1)<<axis_v1v2_cv.x,axis_v1v2_cv.y,axis_v1v2_cv.z);cv::Mat rotation;
cv::Rodrigues(R_vec,rotation);
std::cout<<" rotation  CV::"<<rotation<<std::endl;for (size_t i = 0; i < locations.size(); i++)
{cv::Mat Pt=(cv::Mat_<double>(3,1)<<locations[i][0],locations[i][1],locations[i][2]);cv::Mat afterPt=rotation*Pt;std::cout<<"orignal     "<<locations[i].transpose()<<"      cv  Translate   "<<afterPt.t()<<std::endl;}

（Eigen法）

Eigen::AngleAxisd ro_vector(-theta, Eigen::Vector3d(axis_v1v2.x, axis_v1v2.y, axis_v1v2.z));
Eigen::Matrix3d ro_matrix = ro_vector.toRotationMatrix();
std::cout<<"rotation eigen "<<ro_matrix<<std::endl;std::vector<Eigen::Vector3d> new_points;
double sum  = 0;
for(int i = 0; i<locations.size(); i++)
{Eigen::Vector3d newP;//计算点到平面上的距离，只处理那些距离平面距离很小的点。double x = locations[i].x();double y = locations[i].y();double z = locations[i].z();//计算每一个真实点到拟合出来的平面的距离，求出总距离，求解平均距离double dist2 = (a*x + b*y + c*z+d)*(a*x + b*y + c*z+d);sum =+ std::sqrt(dist2); newP.x()=x;newP.y()=y;newP.z()=z;Eigen::Vector3d new_point = ro_matrix*newP;std::cout<<"newP: "<<new_point.transpose()<<"    orignal"<<newP.transpose()<<std::endl;      }

根据上面的步骤，我们就可以将拟合出来的平面旋转到参考平面。

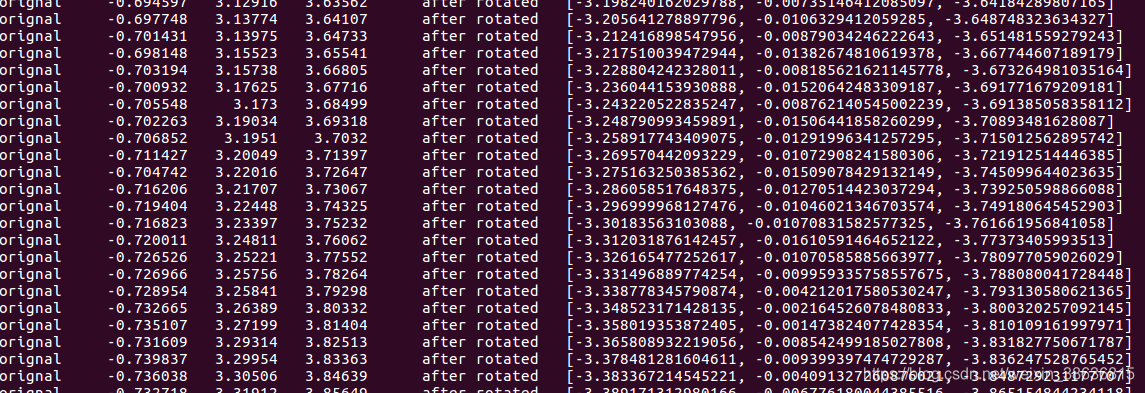
如何验证我们的旋转对不对呢，你可以检验经过旋转之后的3D点是不是某一个维度上的值全部稳定在一个值附近。下图中y轴的值稳定在比较小的值，这样

我们取出x和z轴上的两维坐标去画图，得到的轨迹失真性更小。

 

三、将旋转后的3D平面画在图像上

将轨迹点画到图像上，其中一个重要的思想就是点坐标的转换。

在下面段代码中，将原始轨迹点按照求解出来的旋转变换，进行旋转，旋转到平行于指定的坐标平面。并且求出实际点的最大值和最小值（作用在下文中有体现）

double min_x = 10e5;
double max_x = 10e-5;
double min_y = 10e5;
double max_y = 10e-5;
for (size_t i = 0; i < locations.size(); i++){cv::Mat Pt=(cv::Mat_<double>(3,1)<<locations[i][0],locations[i][1],locations[i][2]);cv::Mat afterPt=rotation*Pt;double x = afterPt.at<double>(1,0);double y = afterPt.at<double>(2,0);plane_points.push_back(cv::Point2d(x, y));if(min_x > x) min_x = x;if(max_x < x) max_x = x;if(min_y > y) min_y = y;if(max_y < y) max_y = y;//求出这些点中的水平方向的最大值最小值和竖直方向的最大值最小值std::cout<<"orignal     "<<locations[i].transpose()<<"      after rotated   "<<afterPt.t()<<std::endl;}

 step1: 根据实际点的大小计算生成图像的长宽

step2: 将实际点中为负的点，通过减去最小值，转换到正点上

step3: 然后就是把转换后的实际点按照原始比例画在图像上

    //计算实际点水平方向与竖直方向的长宽比值double wh = (max_x-min_x)/( max_y-min_y);//只设置高度，然后根据实际比利计算长度，这样可以确保画出来的轨迹图不失真。int img_height = 720;int img_width = img_height * wh;cv::Mat img(img_height, img_width, CV_8UC3, cv::Scalar(255, 255, 255));std::cout<<"img.size(): "<<img.size()<<std::endl;double scale_ = max(max_x-min_x, max_y-min_y);std::cout<<"scale_: "<<scale_<<std::endl;cv::Point2i center_p;std::vector<cv::Point2i> pixels;for(int i = 0; i<plane_points.size(); i++){//首先将负数部分都转换到正数部分double x = plane_points[i].x - min_x;double y = plane_points[i].y - min_y;//std::cout<<"x: "<<x<<"   y:"<<y<<std::endl;// int u = img_width*x/(scale_);// int v = img_height*y/(scale_);int u = img_width*x/(max_x-min_x);int v = img_height*y/(max_y-min_y);std::cout<<"u: "<<u<<"  v:"<<v<<std::endl;cv::Point2i center_p(u,v);pixels.push_back(center_p);cv::circle(img, center_p, 2, cv::Scalar(0, 0, 255), -1, 8);}for(int i = 1; i<pixels.size(); i++){cv::Point2i start_point(pixels[i-1].x, pixels[i-1].y);cv::Point2i end_point(pixels[i].x, pixels[i].y);cv::line(img, start_point, end_point, cv::Scalar(0, 0, 255), 2);}