题目描述

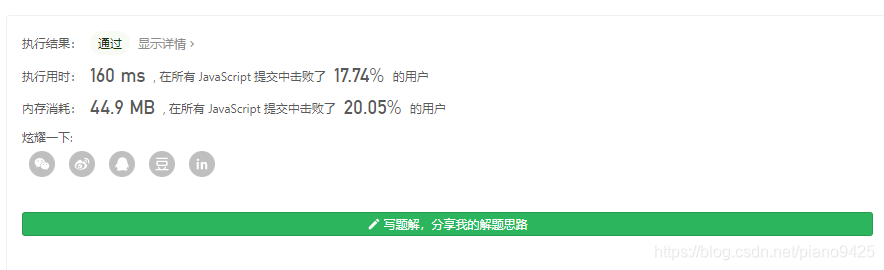
思路1:
- 写一个返回2进制中1数量的函数countOne
- 遍历0到num,对每一个数使用countOne,并将结果保存到res中返回
var countBits = function (num) {let res = new Array(num + 1).fill(0);for (let i = 0; i <= num; i++) {res[i] = countOne(i.toString(2));}return res;
};const countOne = num => {let res = 0;for (let i = 0; i < num.length; i++) {if (num[i] == 1) {res++;}}return res;
}
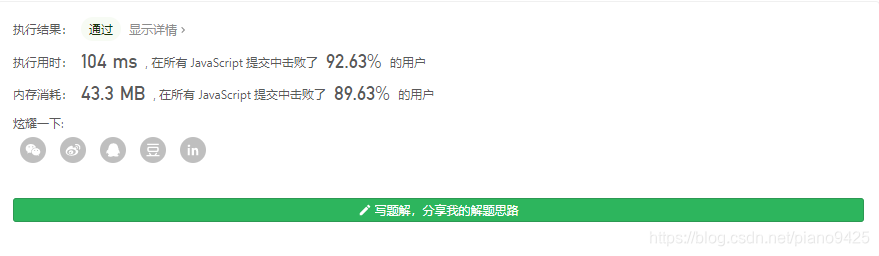
思路2:
- 上面求1的个数的速率可以提升,可以考虑采用位运算来求
var countBits = function (num) {let res = new Array(num + 1).fill(0);for (let i = 0; i <= num; i++) {res[i] = countOne(i);}return res;
};const countOne = num => {let res = 0;while (num > 0) {res++;num = num & (num - 1);}return res;
}
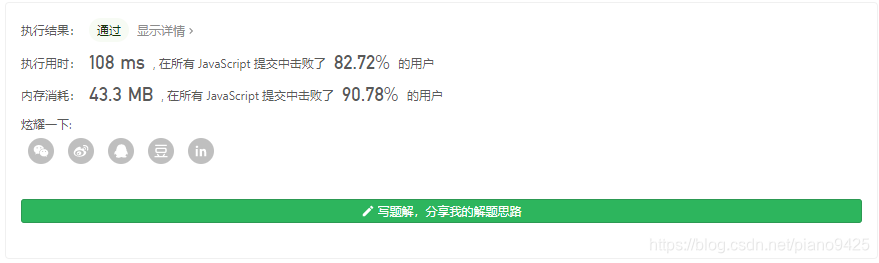
思路3:
找到后面数与前面数的联系,利用缓存进一步加速
- 对于十进制10来说,其对应的二进制为"1010",其1的位数dp[10]为十进制2中1的位数 + 1,其对应公式如下:
dp[10] = dp[2] + 1;
- 10与2之间其实只差一个十进制8(“1000”)
- 同理十进制13(“1101”)其1的个数可以由公式 dp[13] = dp[5] + 1 求出
十进制5的二进制对应"101"
- 因此可以得到递推关系式, dp[i] = dp[i - highBit] + 1;
其中 highBit是不超过i的2的最大整数次幂
算法如下:
var countBits = function (num) {let dp = new Array(num + 1).fill(0);let highBit = 0;for (let i = 1; i <= num; i++) {if ((i & (i - 1)) == 0) {highBit = i;}dp[i] = dp[i - highBit] + 1;}return dp;
};




)






:典型问题分析(Bugfix))







