Problem
bzoj & Luogu
题目大意：
给定序列\(\{a_i\}\)，求一个严格递增序列\(\{b_i\}\)，使得\(\sum \bigl |a_i-b_i\bigr|\)最小
Thought
正序：直接对应
逆序：取中位数（证明：“医院设置”）
最优解一定是分段
每一段台阶式上升
每一段选取中位数
沙漏型左偏树 合并区间 选取中位数
upd:貌似不需要沙漏型？
Solution
前置技能：小学奥数、可并堆
和上面类似，先不考虑严格上升，即先考虑非严格上升
序列一定是要分成若干段，每一段的\(b\)值相等，且后一段比前一段大，像台阶一样（如下图，是一个\(b(x)\)的伪函数）
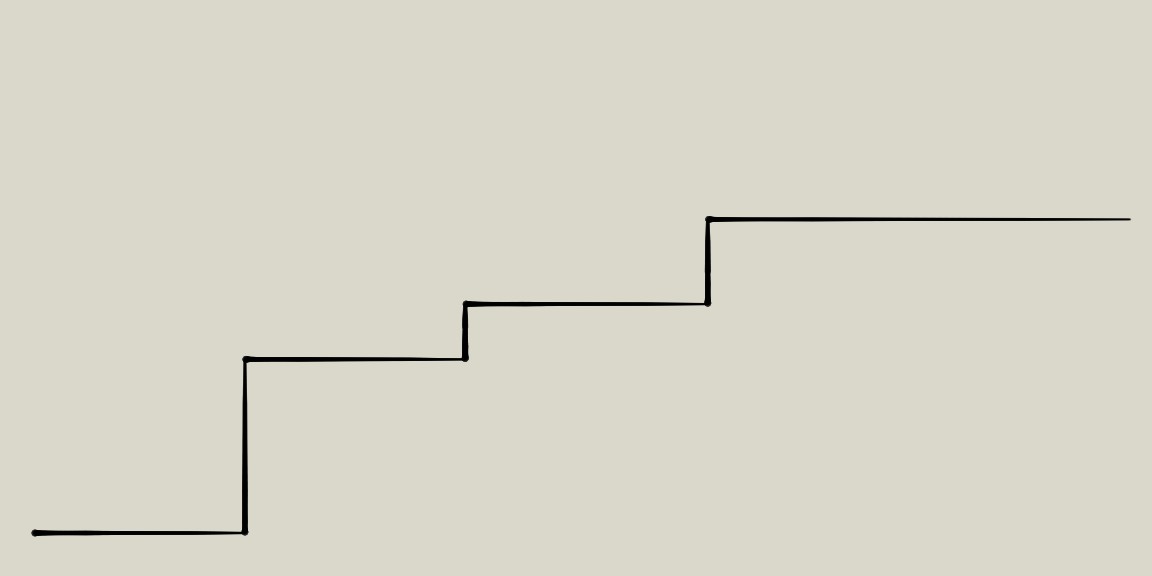
先令\(\forall i\in[1,n],a_i=b_i\)，这样的答案为零，但却不合法，接下来考虑如何用最小代价使答案合法，考虑对于相邻两段数：
设当前前一段取最优值时的\(b\)统一为\(b_1\)，后一段统一为\(b_2\)，变换之后两者的统一\(b\)值分别变为\(b_1^{'},b_2^{'}\)
如果\(b_1\leq b_2\)，则对于这两段来说是合法的，无需操作；
如果\(b_1>b_2\)，则表示因为要求\(b_1\leq b_2\)，而现在是\(b_1>b_2\)，要求\(b_1^{'}\leq b_2^{'}\)，考虑到两段的\(b\)变化得越少越好，即\(\bigl | b_1-b_1^{'}\bigr |,\bigl | b_1-b_1^{'}\bigr |\)取最小，则变换之后\(b_1^{'}=b_2^{'}\)，我们再考虑\(b_1^{'}(b_2^{'})\)的取值，应为这两段数合在一起的中位数，证明见下方“附”，找中位数可以用线段树解决，也可以用堆解决（堆解法见TJOI2010中位数），考虑到两段需要合并，线段树需要线段树合并，而堆只需要可并堆即可
如何把相邻两段的处理扩展到整个序列呢，鉴于整个\(b\)序列是递增的，可以用单调栈实现，栈中的比较方式就是上述对于相邻两段的处理
现在解除一开始自己设置的限制，将\(a_i\)设为\(a_i-i\)即可将非严格上升序列的做法转移到严格上升序列的做法
附：证明：其实就是小学奥数题 对于一段数\(\{c_i\}\)选取\(x\)使得\(\sum \bigl |x-c_i \bigr |\)，最小的\(x\)值的一个取值为\(\{c_i\}\)序列的中位数：
反证法：设原序列有\(n\)个元素，则比\(x\)大/小的数有\(\frac n2\)个，若\(x\)变小或变大，则若越过序列中另一个值时，比\(x\)大/小的数有\(\frac n2±1\)个，统计答案时只会增加\(2\)或不变
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rg registerstruct ios {inline char read(){static const int IN_LEN=1<<18|1;static char buf[IN_LEN],*s,*t;return (s==t)&&(t=(s=buf)+fread(buf,1,IN_LEN,stdin)),s==t?-1:*s++;}template <typename _Tp> inline ios & operator >> (_Tp&x){static char c11,boo;for(c11=read(),boo=0;!isdigit(c11);c11=read()){if(c11==-1)return *this;boo|=c11=='-';}for(x=0;isdigit(c11);c11=read())x=x*10+(c11^'0');boo&&(x=-x);return *this;}
} io;const int N=1001000;
struct Leftist_Tree{int l,r,dis,val;}t[N];
struct node{int l,r,rt,sz,val;node(){}node(const int&L,const int&id){l=L,r=rt=id,sz=1,val=t[id].val;}
}h[N];
int n,top;inline int merge(int u,int v){if(!u||!v)return u|v;if(t[u].val<t[v].val||(t[u].val==t[v].val&&u>v))swap(u,v);int&l=t[u].l,&r=t[u].r;r=merge(r,v);if(t[l].dis<t[r].dis)swap(l,r);t[u].dis=t[r].dis+1;return u;
}inline int del(int u){return merge(t[u].l,t[u].r);}void work(){io>>n;for(rg int i=1;i<=n;++i)io>>t[i].val,t[i].val-=i;h[top=1]=node(1,1);for(rg int i=2;i<=n;++i){int l=h[top].r+1;h[++top]=node(l,i);while(top^1&&h[top-1].val>h[top].val){--top;h[top].rt=merge(h[top].rt,h[top+1].rt);h[top].r=h[top+1].r;h[top].sz+=h[top+1].sz;while(h[top].sz>((h[top].r-h[top].l+2)>>1)){--h[top].sz;h[top].rt=del(h[top].rt);}h[top].val=t[h[top].rt].val;}}return ;
}void Print(){ll Ans=0;for(rg int i=1,p=1;i<=n;++i){if(i>h[p].r)++p;Ans+=abs(h[p].val-t[i].val);}printf("%lld\n",Ans);for(rg int i=1,p=1;i<=n;++i){if(i>h[p].r)++p;printf("%d ",h[p].val+i);}putchar('\n');return ;
}int main(){work();Print();return 0;
}
