(Review cs231n) Backpropagation and Neural Network

损失由两部分组成：

数据损失+正则化损失（data loss + regularization）

想得到损失函数关于权值矩阵W的梯度表达式，然后进性优化操作（损失相当于海拔，你在山上的位置相当于W，你进行移动，需要知道你到底是向下走了还是向上走了，所以可通过梯度或者是斜率来知道，你的目标是不断的移动你的W就是位置，使你找到谷底就是损失最小的，但是有可能会存在你找到局部的谷底，就是所谓的局部最优)。

我们使用梯度下降算法，进行迭代运算，计算梯度进行权值的更新，一直循环执行这个操作，最后会停留在损失函数的低值点相当于在训练数据集上的最好表现。

梯度下降

1. 数值梯度

写起来容易但是运算太慢，使用微积分很快但是可能会有错误，所以我们需要进行梯度检查，先通过运算得到解析梯度，然后使用数值梯度二次检查他的准确性

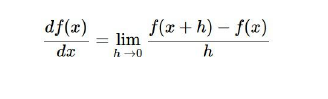
2. 计算图（computational graph）

使用运算图的形式表现出来显得十分的庞大，below is the computational graph of SVM.

如果是卷积神经网路，这个计算图会非常的庞大，所以想把计算图(运算表达式)都写下来并不实际，计算图会不断的重复运行，表达式不现实，时间的耗费，所以:

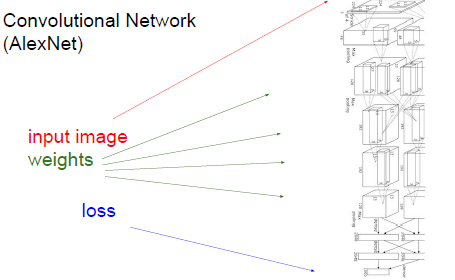
用一些函数将中间变量转换成最终的损失值，结合输入和梯度来得到最终的损失函数。

例子：f(x,y,z) =（x+y）z

基于这些输入得到表达式的梯度，引进中间变量q，表达式将变为一个加法式和一个乘法式，则转变为了f=qz,分别求出f对x,y,z的偏导，在计算图中我们对所有的中间变量都进行求偏导的计算，知道我们建立的表达式是使梯度基于输入值的一个公式。

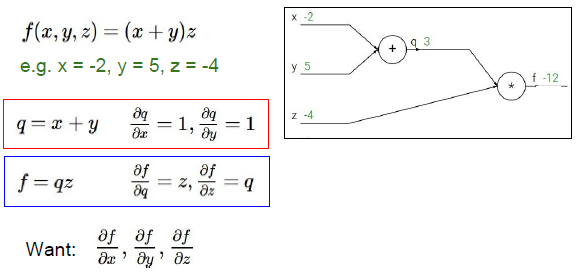
从右端开始作为递归运算的起点：

1. 先考虑f对f的偏导，为一个identity function 值为1, 所以这个恒等函数的梯度为1

2. 考虑f对z的偏导，是中间变量q，即x+y, 梯度为3，说明了z对最终结果是积极的影响，也就说给z一个小增量h，整个运算图的输出结果也会增加3h，

3. 考虑f对q的偏导，求得的结果是z，值为-4，如果给q一个小增量h,那么运算图的输出结果会减少4h，因为斜率是-4.

4. 计算y的梯度，求得的结果是-4，遵守链式法则，乘积运算，q中y的梯度和f中q的梯度相乘，这可以看作是反向传播的体现。x和y的导数都为1，x、y对q都有正向的影响。斜率为1，对x加上增量h，q也会增加h，最终y影响到整个运算图的输出结果，所以你将y对q的影响和q对最终损失的影响相乘，进行递归在整个运算图，增加y会使得运算图的最终结果以4倍的速率减少，使最终结果减少。

整个计算图非常的庞大，输入集x、y和输出集z，进行反向的递推。

可以得到局部梯度，对她们进行只是加法或乘法，x和y对于输出值的影响。

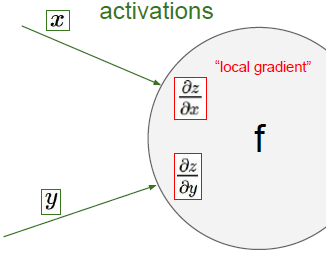
因此，我们只要得到最终的损失，就可以逆推回去，运算链路的最终输出的影响到底有多大。要知道dl/dz这个梯度的流向是反向的的。

要得到结合输入与梯度得到最终损失的关系，dL/dx=dL/dz*dz/dx，局部梯度与loss与输出的梯度相乘，x对于该运算链路最终结果的影响如下图所示，所以根据链式法则输出结果的全局梯度乘以局部梯度，并且通过后者来改变他，y也一样。记住这些X和Y不是来自于同一个运算，所以你要将这一法则运用在整个的运算链路中，也因此这些参数对最终损失的影响都是相互的。她们会告知彼此，如果这是一个正的梯度，那么损失将会随着他们增大而增大，如果是负梯度，那么损失将会随着他增大而减小，并且他将链路中的所有局部梯度相乘，这个过程叫做反向传播。

在运算链路中，这是一种通过链式法则来进行递推的计算过程，这个链路中的每个中间变量，都会对最终的损失函数产生影响。

补充知识，导数与斜率的关系（感谢美丽的闫小姐提供的公式推导❤）

例子：

这个运算链路是一个二维的sigmoid函数，计算每一个输入量对这一表达式的最终输出的影响，这里计算他的梯度。

知道了每个小运算的局部梯度，我们在运算的时候可以直接使用他们（求导等于梯度），

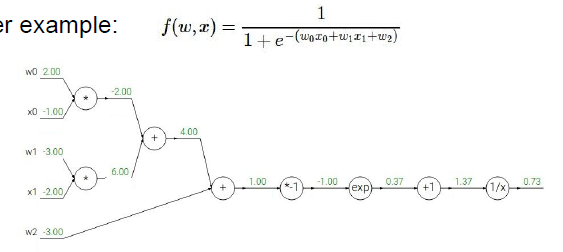
1. 从最后的梯度开始，写上1，递归的开始，这是恒等函数的梯度

2. 1/x进行反向传播，

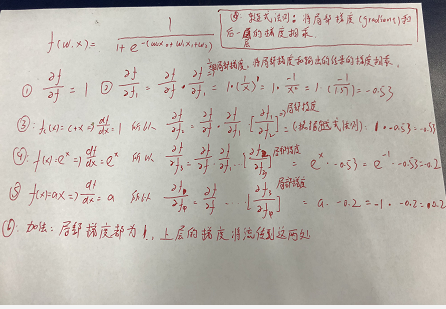
重要：

　　　1.根据链式法则，输入到损失的梯度等于，局部梯度乘以后一层的梯度。

　　 2.经常遇到所有输入的局部梯度都为1，不管后面的是多少，都将自身的梯度平均分发给他的输入，根据链式法则，都乘以1，无影响。

　　 3.加法就像一个梯度分发器，如果从前面得到一个梯度，分发所有梯度。

　　 4. 反向计算时首先要得到所有的参数，比如所有的输入和最终的损失函数，我们用正推法计算损失函数，然后再用反向传播算法，对每一层运算计算（loss）对输入的梯度，反向传播算法就是多次不同的使用链式法则

　　 5. 反向传播通常慢于正向传播。

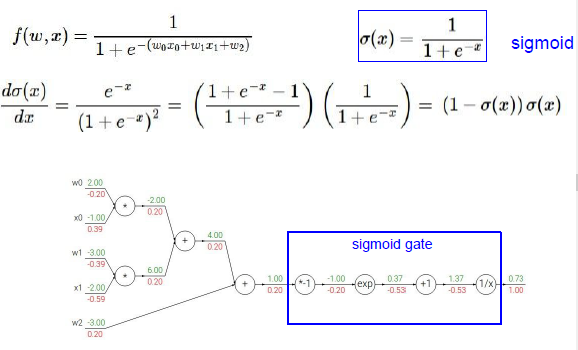
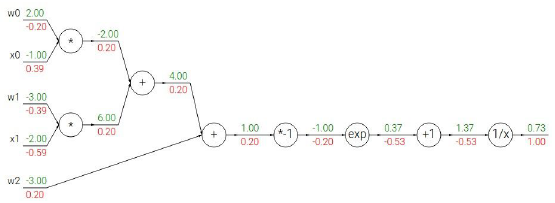
　　将sigmid的梯度表示为只有sigmoid函数的运算，那么就可以只进行一次sigmoid运算，然后只需要计算出sigmoid函数的局部梯度(1-sigmoid(x))sigmoid(x)就可以了(意思就是其实大的函数也可以直接视作一个整体计算梯度)，所以我们把它放在整个计算图中。

　　一旦我们知道怎么计算局部梯度，通过链式法则和各部分之间乘法，其他一切都能求得，蓝色框我们可以反向传播通过S门，看起来输入1，输出是0.73，其实0.73就是sigmoid(x)值，通过之前sigmoid的梯度公式，得到sigmoid的局部梯度，正好这是在回路的尽头，要乘以1.0 .

　　通常我们把整个表达式拆分开来，一次只计算一部分部分，或者把这部分看作是一个S门，这取决于我们打算把整个表达式拆分到何种程度(BP的拆分粒度)，所以局部梯度容易得到，我们整个看作一个S门。

　　当你看到一些运算部分要重复进行并且局部梯度很简单，就可以组成一个合并单元。

　　通过计算图，可以直观的理解梯度是如何在整个神经网络流动的，通过理解梯度的传递过程可以让你了解一些问题，比如梯度消失的问题

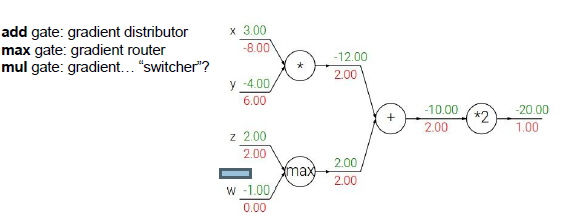
　　加法门：局部梯度为1，对两个输入的梯度都为2,梯度分配器，分配相等的梯度值。

　　最大值门：梯度路由，如果是一个简单的二元表达式Max(x,y),这就是最大值运算门，求x,y上的梯度，那么你认为较大的输入梯度为1（局部梯度），较小的对输出没有影响。反向传播时，它会把梯度值分配给输入值最大的线路，这就是梯度路由。

　　乘法门：梯度转换器，

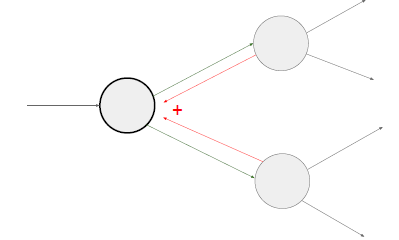
　　一个值通过分支被用于各部分的计算中，通过多元链式法则，正确的计算方法是把他们的结果相加，在反向传播过程中，它们的梯度值也是相加的。

　　使用计算图，构建神经网络，在这些运算门的基础上，我们需要确定整个图的连接结构，哪些门相互连接，这些通常是在一个图像或者网络对象中说明的，这个对象有这两部分，前向传播和后向传播，这是伪代码：

思路：遍历网络中所有的运算门，并按正确的逻辑顺序进行排列，意味着所有的输入值在运算之前要知道这些标注信息，也就是从左到右的排列，要在各个门进行前向运算，并且由这个网络对象确保各个部分按顺序正确连接，

　　而反向传播按照相反顺序进行，反向传播经过各个门，各个门之间的梯度相互传递，并计算出分解开的各梯度值，事实上网络对象就是对这些门进行简单的封装，以后发现这些门会被称作层，对各层结果的简单封装。

运算门的实现，定义一个类：最终求得整个损失函数关于各个变量的梯度，L关于z的偏导就是我们要求的值，这由dz代表，这所有的变量都是标量，dz也是数字，表示输入在回路最后的影响。

计算图中各个门之间的梯度可以正确传递，反向传播中，如果由支路合并，就要把所有梯度相加，所以在前向过程中，把这些大量的数据存储下来，反向可能会用，如果在正向过程中存储的了局部梯度值，那么就不需要记住其他中间值，需要利用各运算门及偏置值在反向运算之前记住所需值，

x1 class MultiplyGate(object):
 2     
 3      def forward(x,y):
 4             z = x*y
 5             self.x = x # 需要记住输入值和其他出现过的中间微分值
 6             self.y = y
 7             return z
 8      def backward(dz)  # dz= dl/dz
 9             dx = self.y * dz # dl/dz * dz/dx
10             dy = self.x * dz # dl/dz * dz/dy
11             return [dx,dy]