如何寻找无序数组中的第K大元素？

有这样一个算法题：有一个无序数组，要求找出数组中的第K大元素。比如给定的无序数组如下所示：

如果k=6，也就是要寻找第6大的元素，很显然，数组中第一大元素是24，第二大元素是20，第三大元素是17...... 第六大元素是9。

方法一：排序法

这是最容易想到的方法，先把无序数组从大到小进行排序，排序后的第k个元素自然就是数组中的第k大元素。但是这种方法的时间复杂度是O(nlogn),性能有些差。

方法二：插入法

维护一个长度为k的数组A的有序数组，用于存储已知的K个较大的元素。然后遍历无序数组，每遍历到一个元素，和数组A中的最小元素进行比较，如果小于等于数组A中的最小元素，继续遍历;如果大于数组A中的最小元素，则插入到数组A中，并把曾经的最小元素"挤出去"。

比如K=3，先把最左侧的7,5,15三个数有序放入到数组A中，代表当前最大的三个数。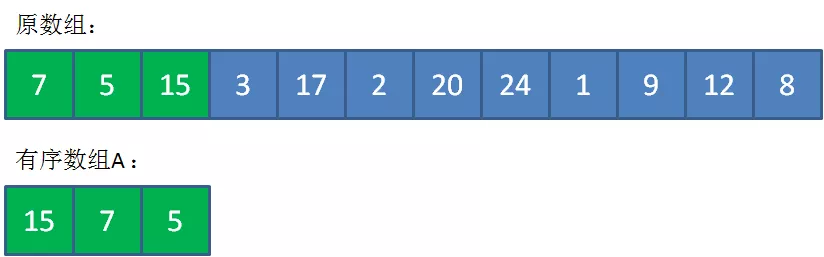

此时，遍历到3时，由于3<5,继续遍历。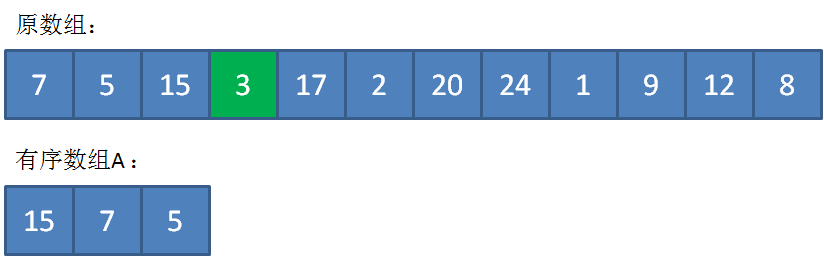

接下来遍历到17，由于17>5,插入到数组A的合适位置，类似于插入排序，并把原先最小的元素5“挤出去”。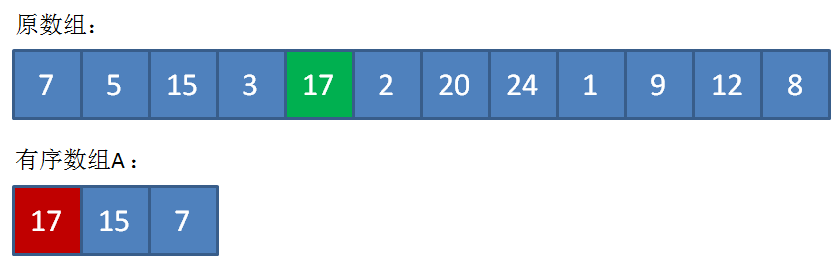

继续遍历原数组，一直遍历到数组的最后一个元素......

最终，数组A中存储的元素是24,20,17，代表着整个数组的最大的3个元素。此时数组A中的最小元素17就是我们要寻找的第K大元素。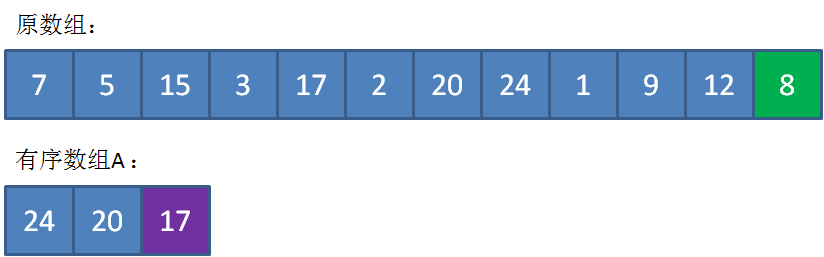

这个方法的时间复杂度是O(nk)，但是如果K的值比较大的话，其性能可能还不如方法一。

小顶堆法

二叉堆是一种特殊的完全二叉树，它包含大顶堆和小顶堆两种形式。其中小顶堆的特点是每一个父节点都小于等于自己的两个子节点。要解决这个算法题，我们可以利用小顶堆的特性。

维护一个容量为K的小顶堆，堆中的K个节点代表着当前最大的K个元素，而堆顶显然是这K个元素中的最小值。
遍历原数组，每遍历一个元素，就和堆顶比较，如果当前元素小于等于堆顶，则继续遍历;如果元素大于堆顶，则把当前元素放在堆顶位置，并调整二叉堆（下沉操作）。
遍历结束后，堆顶就是数组的最大K个元素中的最小值，也就是第K大元素。

假设K=5，具体操作步骤如下：

1.把数组的前K个元素构建成堆

2.继续遍历数组，和堆顶比较，如果小于等于堆顶，则继续遍历;如果大于堆顶，则取代堆顶元素并调整堆。

遍历到元素2，由于2<3，所以继续遍历。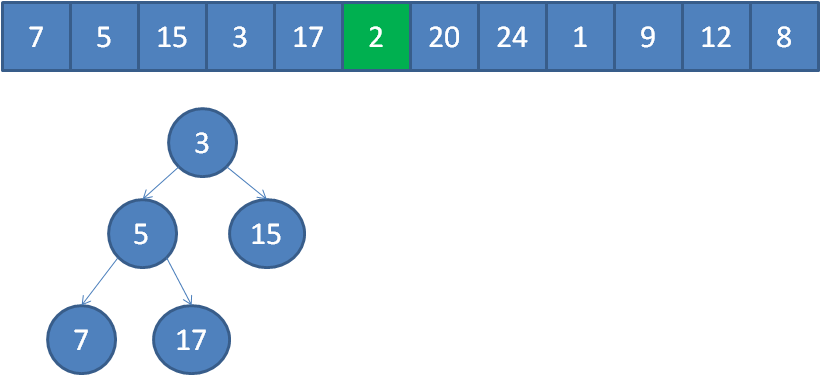

遍历到元素20，由于20>3,20取代堆顶位置，并调整堆。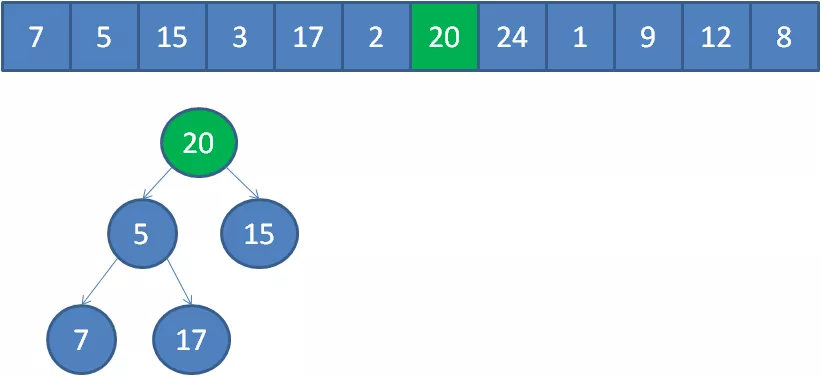

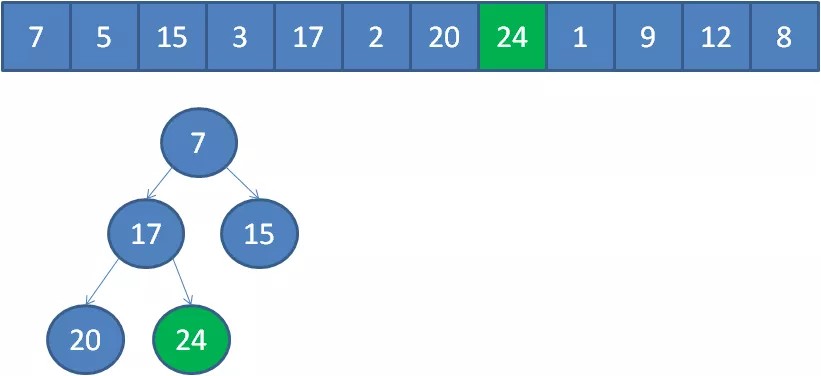
遍历到元素24，由于24>5,24取代堆顶位置，并调整堆。

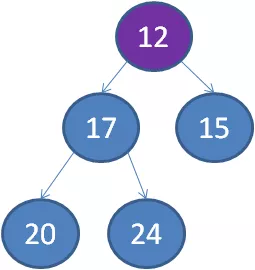
以此类推，我们一个一个遍历元素，当遍历到最后一个元素8时，小顶堆的情况如下：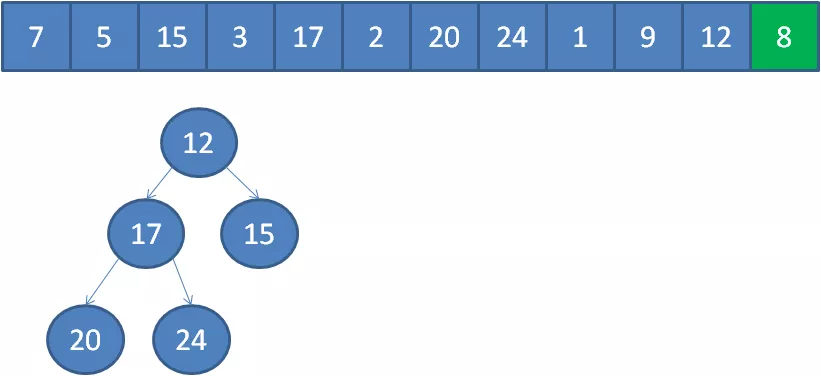

3.此时的堆顶，就是堆中的最小元素，也就是数组中的第K大元素。

这个方法的时间复杂度是多少呢？

1.构建堆的时间复杂度是O(K)
2.遍历剩余数组的时间复杂度O(n-K)
3.每次调整堆的时间复杂度是O(logk)
其中2和3是嵌套关系，1和2,3是并列关系，所以总的最坏时间复杂度是O((n-k)logk + k)。当k远小于n的情况下，也可以近似地认为是O(nlogk)。

这个方法的空间复杂度是多少呢？
刚才我们在详细步骤中把二叉堆单独拿出来演示，是为了便于理解。但如果允许改变原数组的话，我们可以把数组的前K个元素“原地交换”来构建成二叉堆，这样就免去了开辟额外的存储空间。因此空间复杂度是O(1)。

代码如下：

/*** 寻找第k大元素* @param array 待调整的数组* @param k 第几大* @return*/public static int findNumberK(int[] array, int k) {//1.用前k个元素构建小顶堆buildHeap(array, k);//2.继续遍历数组，和堆顶比较for (int i = k; i < array.length; i++) {if(array[i] > array[0]) {array[0] = array[i];downAdjust(array, 0, k);}}//3.返回堆顶元素return array[0];}private static void buildHeap(int[] array, int length) {//从最后一个非叶子节点开始，依次下沉调整for (int i = (length - 2) / 2; i >= 0; i--) {downAdjust(array, i, length);}}/*** 下沉调整* @param array 待调整的堆* @param index 要下沉的节点* @param length 堆的有效大小*/private static void downAdjust(int[] array, int index, int length) {//temp保存父节点的值，用于最后的赋值int temp = array[index];int childIndex = 2 * index + 1;while (childIndex < length) {//如果有右孩子，且右孩子小于左孩子的值，则定位到右孩子if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {childIndex++;}//如果父节点小于任何一个孩子的值，直接跳出if (temp <= array[childIndex])break;//无需真正交换，单项赋值即可array[index] = array[childIndex];index = childIndex;childIndex = 2 * childIndex + 1;}array[index] = temp;}public static void main(String[] args) {int[] array = new int[] {7, 5, 15, 3, 17, 2, 20, 24, 1, 9, 12, 8};System.out.println(findNumberK(array, 5));}