一、实践题目
改写二分搜索算法
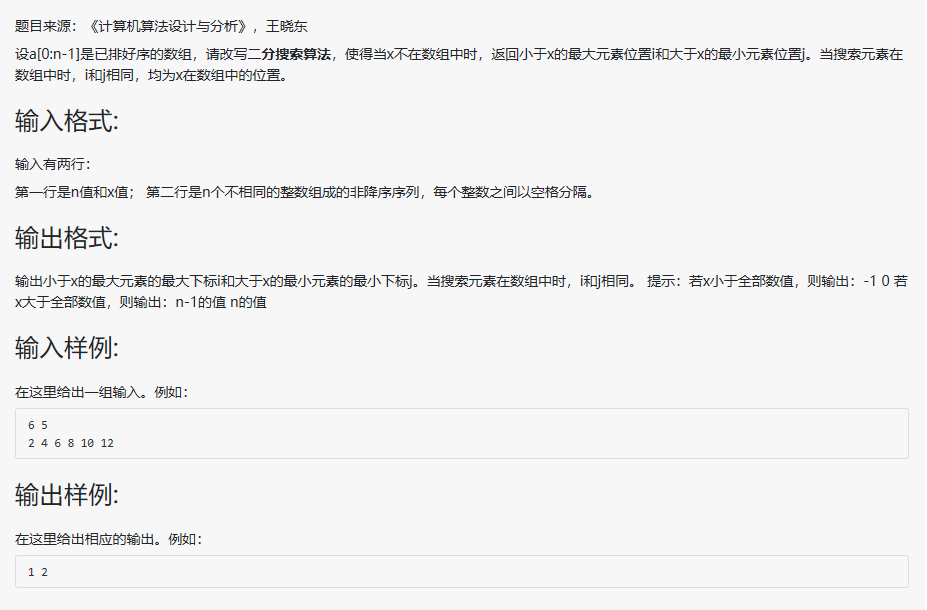
二、问题描述
这道题目主要是考验同学们在熟练掌握二分搜索法的前提下,对二分搜索的结构和运用有一个更加深刻的掌握。首先是要了解二分搜索的结构,其次,要了解二分搜索中的分治方法每一个步骤的用意,对于题目中的要求要有一个清晰的在哪个位置、以哪个为条件的认知。
三、算法描述
二分搜索法充分利用了元素间的次序关系,采用分治策略,在时间复杂度较低的情况下完成搜索任务。
二分搜索法的基本思想是在升序数组a[n]中查找x,将n个元素大致分成两半,将x与a[n/2]比较。若x = a[n-2],则找到x,算法终止;若x > a[n/2],则要向a[n/2]的右边方向继续寻找;若x < a[n/2],则要向a[n/2]的左边方向继续寻找。
a[left] a[n/2] a[right]
| 1 | 2 | 3 | …… | n-1 | n |
继续搜索时缩小范围,我们可以以x < a[n/2]举个例子,此时搜索范围是在[ a[left], a[n/2 -1] ]之间,之所以是n/2-1,是由于在第一轮中我们已经对x和a[n/2]做了对比,此时再做一次未免多此一举,与会增加算法的时间复杂度。这时,范围的a[mid]值为a[(0 + n/2 - 1) / 2] ,我们可以将x与a[mid]对比。若x=a[mid],则得到结果,算法结束;若x>a[mid],则要向mid的右边方向继续寻找;若x<a[mid],则要向a[mid]的左边方向继续寻找。
a[left] a[mid] a[n/2-1]
| 1 | 2 | …… | a[n/2-1] | a[n/2] |
…………
以此类推,直到找到最后一个a[mid]的值,此时x已知的范围已经分无再分,可以用来作为后面对x在a[n]中位置的评判标准。若x>a[mid],则x的值会在a[mid]和a[mid+1]之间;若x<a[mid],则x的值会在a[mid-1]和a[mid]之间。
至于特殊情况若x小于全部数值或者x大于全部数值,可以在 x在数组中、x不在数组中但有左右范围 这两种if语句出现之前考虑。
具体代码如下:
#include<iostream> using namespace std; int a[1005], n, mid; int mark = 0; int find(int *a,int x){int l = 0;int r = n - 1;while(l <= r) {mid = (l + r) / 2;if(x == a[mid]) {mark = 1;return mid;}if(x > a[mid]) l = mid + 1;else r = mid - 1;}return mid; } int main() {int x;cin >> n >> x;for(int i = 0; i < n; i++) {cin >> a[i];}int ans = find(a, x);if(a[n-1] < x) cout << n - 1<< " " << n;if(a[0] > x) cout << "-1 0";if(mark == 1)cout << ans << " " << ans << endl;else{if(a[ans] > x)cout << ans - 1 << " " << ans;else cout << ans << " " << ans + 1;} return 0;}
四、算法时间及空间复杂度分析
时间复杂度:输入a[n]时时间复杂度为n + find函数的时间复杂度为O[logn] + 判断x在数组中位置时比较了5次,所以综合起来最终这个算法的时间复杂度为O[logn]。
空间复杂度:这个算法主要使用的辅助空间单元的个数只有一个,所以空间复杂度为O[1]。
五、心得体会
1.一开始我对于二分搜索法运用地不是十分熟练,但是在我自己打过代码之后,逐渐明白了它的结构框架就是分而治之。在此之上,难弄懂的题目要求在纸上演算过几次之后,对于如何设计算法就会胸有成竹。
2.我和我的搭档在做第一题时浪费了很多时间,是由于在极端情况下总是达不到要求。我在我的搭档那里学到了如何运用简单的步骤来检验自己代码中出的错误,只要不断地带入数值,输出其中的一个过程相关的值,就可以较为快捷地找到自己的错误在哪里。








)




)

)



