
点
为什么要用R
计量经济学作为经济大类下一门非常实用的学科有很强的实践意义。尽管内容庞杂但基本的指导思想却很简单,因此通过一门统计编程语言学习、掌握计量经济学有很大的益处。
目前,市面上已经有多款统计编程语言和统计软件,实证分析领域中STATA始终坐稳第一把交椅,相关的书籍与课程也汗牛充栋。(陈强 2015)(赵西亮 2017)但STATA毕竟是一个在学术圈范围内比较热门的商业软件,在未来可迁移至工作中的效率便不是很高,同时STATA在处理一些复杂的数据或时间序列时,软件的限制也会导致工作效率的下降。而R语言在此类问题上便有较大的优势,在处理高频时间序列时其效率便远高于STATA,对于大数据操作而言,也不会受到STATA不同发行版本的限制。
随着RStudio的发布以及Rmarkdown的开发日趋成熟,利用R进行可复用,甚至整合数据操作与文章写作变成了可能,本文也是利用Rmarkdown完成的教学参考资料,其数据操作与统计分析皆在Rmarkdown中完成。
考虑到上述的优点,笔者认为利用R语言学习计量经济学是一种效率高、回报高的学习过程。本文主要关注R语言在计量经济学中的应用,以及在数据挖掘中的应用(如果以后想写的话),因此对于R语言本身的特性不做系统性展开,但会在需要的时候进行适当的解释与说明。
回归:计量经济学的灵魂
我发现空手道不是掌握那4000个动作就能学好的。想要学好它,关键在于你能不能把那些基本动作不断反复地操练4000遍。
对于计量经济学而言,这个“基本动作”有两种普遍的观点。第一种是由(Angrist and Pischke 2014) 主推的随机试验方法, 第二种则是大部分计量经济学教材中采用的,将线性回归作为计量经济学的基础。从实用性的角度来说,线性回归是非常优秀的解释方案,而随机试验与匹配统计则显得挖掘的太过深入,不适合作为本文的逻辑起点。
不要问,问就是做个回归
为什么线性回归那么受人喜爱,最主要的原因在于线性回归的可解释性是目前为止最直观,最清晰的。另一方面,线性回归的解决方案到目前为止也是最清晰、最简明的方案。不妨考虑劳动经济学的经典案例,即教育水平对工资的影响(Wooldridge 2016):
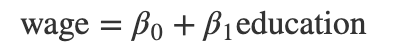
在理想状态下(即满足了线性回归的假设条件后),系数\beta_1可以解释为每增加1年教育,工资的增量。但现实状态下,工资显然不仅仅受到教育年限的影响,这时候线性回归的另一个优势就显现了出来,即线性回归的系数\beta_1(在理想状态下)代表了在控制了其他因素不变的情况下,对于工资的影响。其理论推导也很简单,不妨引入另一个会对工资产生影响的变量,工作年限workingAge,上述方程即变为

此时,系数beta1代表了教育年限的边际影响,不受到工作年限的影响,即有:
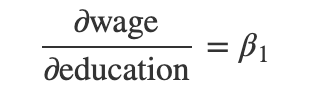
如何估计线性回归的系数?目前最通用、最优的方案依然还是最小二乘法(OLS)。(陈强 2015)
牛刀小试,我们做个回归
针对上述讨论的内容,通过R语言便可以很容易实现。对R语言而言,完成一个统计回归一般分为以下3步:
- 导入数据
- 清洗数据
- 做个回归
这个例子中并不涉及清洗数据,因此只需要导入数据即可。
library(haven) #read_dta使用了haven包,因此需要导入haven
#导入数据,数据来源为伍德里奇《计量经济学导论-现代观点》中的数据集
WAGE1 "WAGE1.DTA",sep = ""))完成数据导入后,由于本节不涉及清洗数据,因此直接对方程进行回归。
wage_LM #回归方程命令
summary(wage_LM) #回归结果##
## Call:
## lm(formula = wage ~ educ + exper, data = WAGE1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.5532 -1.9801 -0.7071 1.2030 15.8370
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.39054 0.76657 -4.423 1.18e-05 ***
## educ 0.64427 0.05381 11.974 < 2e-16 ***
## exper 0.07010 0.01098 6.385 3.78e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.257 on 523 degrees of freedom
## Multiple R-squared: 0.2252, Adjusted R-squared: 0.2222
## F-statistic: 75.99 on 2 and 523 DF, p-value: < 2.2e-16到这一步为止,我们已经完成了一次回归,但有两个亟待解决的问题。
- 回归结果很难看,不直观
- 上述情况下都是理想状态,那么什么是不理想状态?
第一个问题很容易解决,可以通过引入其他美化输出结果的工具解决。第二个问题则留到下一节进行分析。
library(stargazer) #引入stargazer包,类似于STATA中的outreg2
stargazer(wage_LM, title = "线性回归结果",
header = F, type = "latex")什么是不理想状态?
一般来说,不理想状态有四种状态,其中内生性由于可以单独成册、且与最小二乘法无本质联系故按下不表,其他三个与最小二乘法密切相关。这三个分别是:
- 共线性
- 自相关
- 异方差
共线性
共线性是所有不理想状态中影响最低的一个因素,一般来说,只要变量之间不存在完全的共线性,即对于变量x1与x2而言,只要x1=a+b x2不严格成立,即可以避免完全共线性的影响。
自相关
自相关往往伴随着两种情况出现。第一种情况是时间序列中的自相关,举例来说,今天的股票价格变动很可能和昨天的股票价格变动有关系。这种自相关是时间序列中要解决的一大问题,一般通过滞后项解决。第二种情况是空间溢出中的自相关,举例来说,上海地区的房价本身就会存在相关性。这种自相关直接导致了空间计量经济学(Spatial Econometrics)的诞生,但也可以通过其他的方式,如增加控制变量解决。一般来说,当自相关出现时除了上述的两个解决方案以外,还可以通过聚类稳健标准误的方法解决。
异方差
异方差的分析在初级计量经济学中占据了大量篇幅,之所以如此,是因为异方差出现会导致对系数检验的统计量失效,即导致了后续置信度的变化。如果单纯只是关心系数,那么异方差并不会影响结果,得出的系数依然无偏估计量。异方差直观来说,便是扰动项方差不再是一个常数,而是依赖于i。定性来说,同方差条件下,残差基本是随机的;异方差条件下,残差则会出现明显的函数特性。
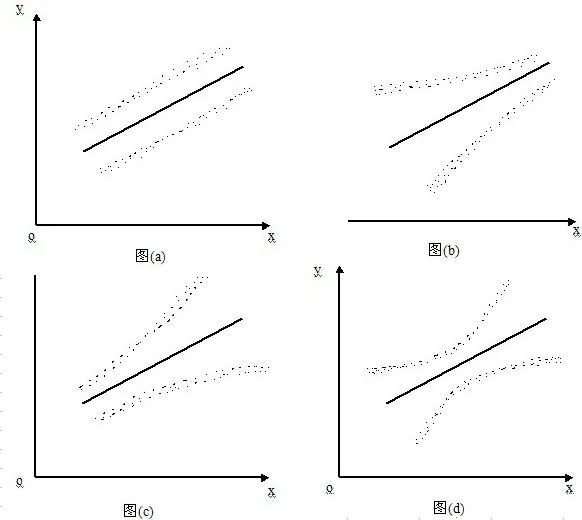
对于上文回归的结果,同样可以通过作图的方式定性地看其是否符合同方差假设。从图中不难发现,上文回归的结果还是存在异方差的情况。
plot(wage_LM, which = 1)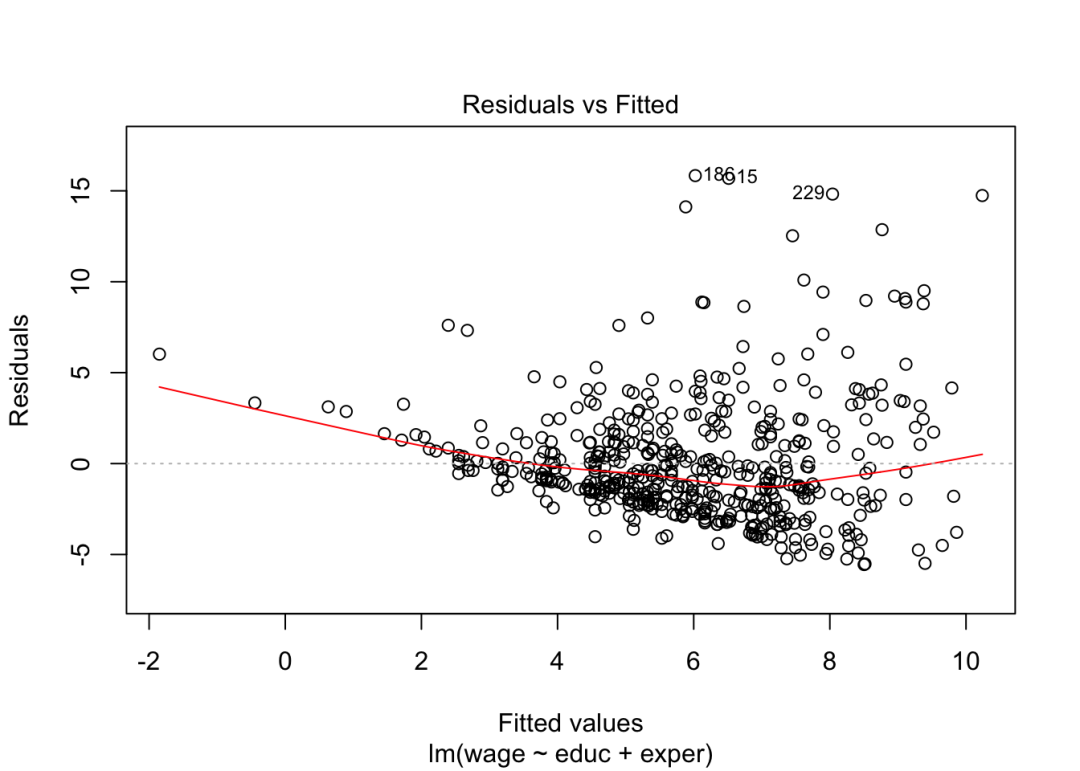
对于异方差的解决则存在多种方法。从理论的角度来看,广义最小二乘法(GLS)才是BLUE(最优线性无偏统计量)。但从实操的角度来看,这个方法可能并不经济。之所以说其不经济的原因在于通过最小二乘法获得的结果是无偏的,只是其检验统计量无效,因此更换统计检验量便可以解决该问题。目前,做实证分析的数据往往已经有充足的数据量,因此直接采用稳健标准误(Eicker 1967)修正统计量的有效性即可。
经典:电力部门的规模报酬
每每写到实证论文部分,尤其是利用最小二乘法的文章,Nerlove(1961)是一篇完全无法回避的经典文章,这篇文章也成为了诸多计量经济学教材中必定录取的参考文献。(Nerlove 1963)(Wooldridge 2016)(Hayashi 2000) 这篇文章想要度量的是美国电力供应行业规模报酬效应(Nerlove 1963),对应的产出范围又是多少。由于本文十分经典,其数据集也已经成为了公开数据集,可以直接在R内引用。
psych::describe(nerlove)[,c("n","mean","sd","median","min","max")]n | mean | sd | median | min | max | |
|---|---|---|---|---|---|---|
| tc | 145 | 12.9760965 | 19.7945767 | 6.7540002 | 0.0820000 | 1.394220e+02 |
| q | 145 | 2133.0827586 | 2931.9421310 | 1109.0000000 | 2.0000000 | 1.671900e+04 |
| pl | 145 | 1.9765517 | 0.2300404 | 2.0000000 | 1.5000000 | 2.300000e+00 |
| pf | 145 | 26.1765517 | 7.8760714 | 26.8999996 | 10.3000002 | 4.280000e+01 |
| pk | 145 | 174.4965517 | 18.2094771 | 170.0000000 | 138.0000000 | 2.330000e+02 |
| lntc | 145 | 1.7246633 | 1.4217234 | 1.9101349 | -2.5010359 | 4.937505e+00 |
| lnq | 145 | 6.5566511 | 1.9127924 | 7.0112138 | 0.6931472 | 9.724301e+00 |
| lnpf | 145 | 3.2088584 | 0.3589002 | 3.2921262 | 2.3321440 | 3.756538e+00 |
| lnpk | 145 | 5.1567768 | 0.1003898 | 5.1357985 | 4.9272537 | 5.451038e+00 |
| lnpl | 145 | 0.6743732 | 0.1197522 | 0.6931472 | 0.4054651 | 8.329091e-01 |
1-10 of 10 rows
数据中,tc为总成本,q为产出数量,pl为劳动价格,pf为燃油价格,pk为资本价格。在估计的过程中,Nerlove从Cobb-Douglas产出函数开始设定模型。
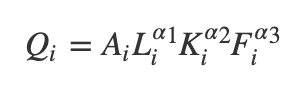
模型中,Q代表了i公司的产出,L代表了i公司的劳动投入,K代表了i公司的资本投入,F代表了i公司为了发电投入的燃油。A则代表了不同公司的不可观察的产出效率。方程 衡量了规模效应。由于电力部门的产出即为需求,因此电力部门的收益最大化即成本最小化,可以概述为以下的优化条件:

于是对于公司i而言,其Cobb-Douglas成本函数便为:
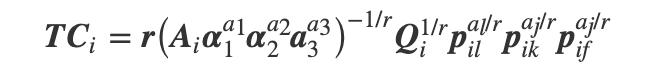
minLiKiFiTCi=pilLi+pikKi+pifFis.t.AiLiα1Kiα2Fiα3=Qi" role="presentation" style=" box-sizing: border-box; line-height: normal; font-size: 14px; word-spacing: normal; overflow-wrap: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial; display: table-cell !important; width: 10000em !important; text-align: left; ">利用自然对数函数的特征,便可以将上述函数变为线性函数。
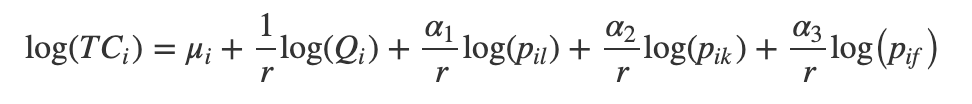
在设定了模型之后,便是对最小二乘法的适用性展开讨论。这也是本文之所以作为经典论文最主要的原因。
- 线性假设:模型形式已经可以说明满足线性假设
- 随机抽样:没有理由怀疑这条不满足
- 不存在完全共线性:这条也是显然的,否则无法回归
- 条件均值为0:这是本文的核心亮点,作者从电力行业的特征入手。一方面,对于投入而言,由于要素价格与公司效率是无关的,因此可以假定要素价格与e_i是独立的。另一方面对于产出而言,电力行业的产出等于需求,而产出价格是由utility commission决定的,根据行业管制的要求来看,这也是与公司效率相独立的。因此可以认为满足零条件均值假设。
- 同方差性:这条其实不满足,但并不影响系数估计,可以看下文的处理。
library(zoo)
library(lmtest)
library(sandwich)
base_reg print(summary(base_reg))##
## Call:
## lm(formula = lntc ~ lnq + lnpl + lnpk + lnpf, data = nerlove)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.97203 -0.23377 -0.01091 0.16185 1.80985
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.56651 1.77938 -2.004 0.047 *
## lnq 0.72091 0.01743 41.352 < 2e-16 ***
## lnpl 0.45596 0.29980 1.521 0.131
## lnpk -0.21515 0.33983 -0.633 0.528
## lnpf 0.42581 0.10032 4.244 3.97e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3923 on 140 degrees of freedom
## Multiple R-squared: 0.926, Adjusted R-squared: 0.9239
## F-statistic: 437.9 on 4 and 140 DF, p-value: < 2.2e-16上面是直接回归得到的结果,为了检验是否满足同方差假设条件,不妨从图示入手。从图中容易发现,残差项的确无法满足同方差条件,而是呈现出了二次函数的状态。
plot(base_reg, which = 1)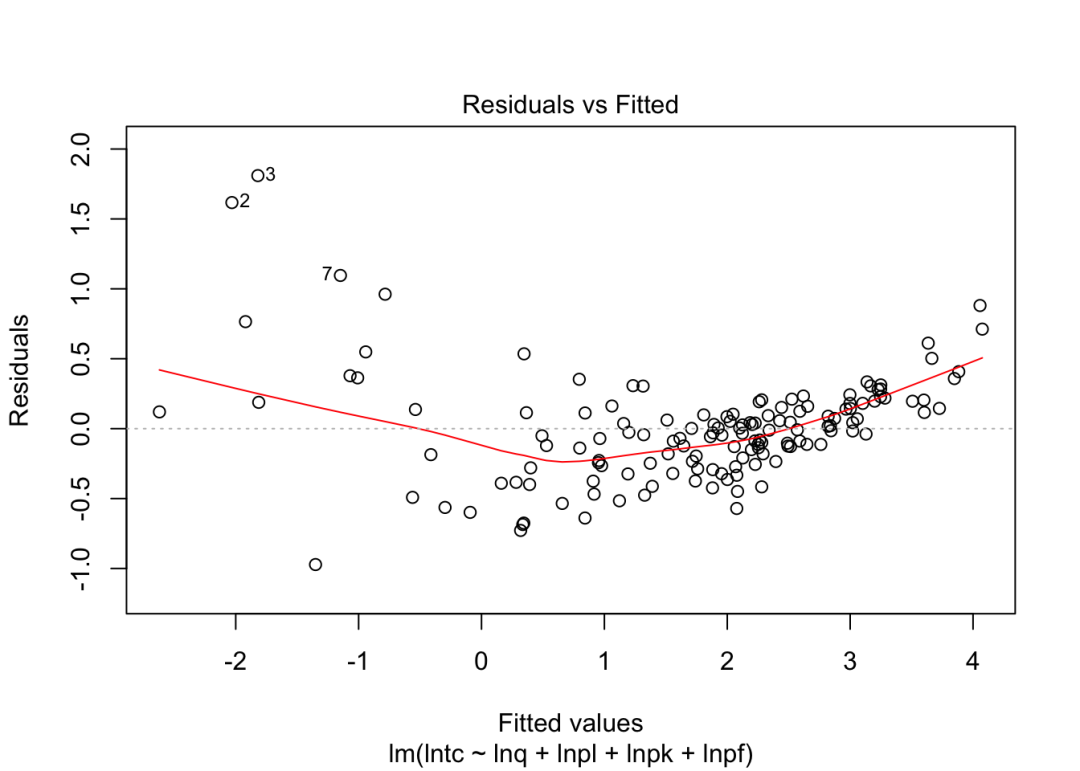
为此,进一步考虑采用稳健统计量进行处理。容易发现,通过稳健统计量进行处理后,估计的系数的确没有变化,而是t统计量产生了差异。
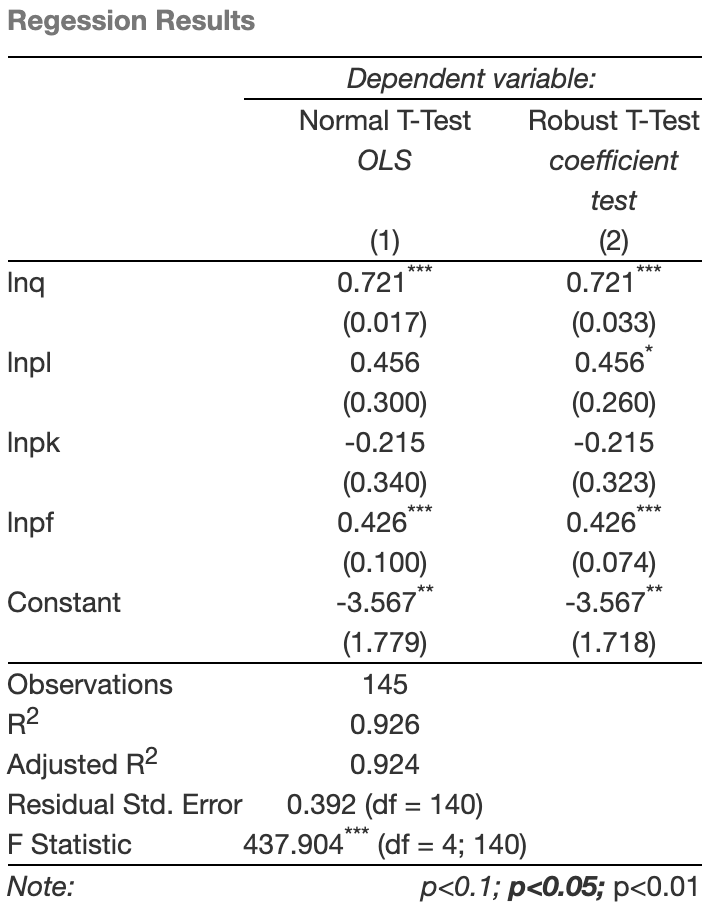
Nerlove也正是通过对最小二乘法中高斯马尔科夫定理成立的五大条件的细致论述,将他的论文流芳百世。对于论文作者而言,Nerlove(1963)最重要的启示是通过产业或研究的数据集的实际情况对计量模型适用性进行分析,分析的过程越充分,那么结果也就越具备说服力,也就可以发更好的期刊。同样细致分析模型的文章还有白重恩(2012)对遗漏变量的解释(白重恩, 李宏彬, and 吴斌珍 2012),未来在分析面板数据模型的时候,也会讲到这篇文章。
结语
本文回顾了计量经济学中最基础的线性回归与最小二乘法,并通过Nerlove(1963)的经典论文大致阐述了一篇优秀的所需要具备的基本条件。通过本文,读者应当能够利用R语言在借助优质的数据集,通过最小二乘法完成一篇相关的计量文章复现。
参考文献
- Angrist, Joshua D., and Jörn-Steffen Pischke. 2014. Mastering’metrics: The Path from Cause to Effect. Princeton University Press.
- Eicker, Friedhelm. 1967. “Limit Theorems for Regressions with Unequal and Dependent Errors.” In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, 1:59–82. 1. Berkeley, CA: University of California Press.
- Hayashi, Fumio. 2000. “Econometrics. 2000.” Princeton University Press. Section 1: 60–69.
- Nerlove, Marc. 1963. “Returns to Scale in Electricity Supply. En ‘Measurement in Economics-Studies in Mathematical Economics and Econometrics in Memory of Yehuda Grunfeld’, Edited by Carl F. Christ.” Stanford University. Press.
- Wooldridge, Jeffrey M. 2016. Introductory Econometrics: A Modern Approach. Sixth edition. Boston, MA: Cengage Learning.
- 白重恩, 李宏彬, and 吴斌珍. 2012. “医疗保险与消费: 来自新型农村合作医疗的证据.” 经济研究 2: 41–53.
- 赵西亮. 2017. 基本有用的计量经济学. 北京大学出版社.
- 陈强. 2015. 计量经济学及Stata应用. 北京: 高等教育出版社.
)



)





)








