刚体的姿态（attitude）有很多种表示方法，关于这个话题有一篇十分出名的综述[1]，也是这篇文章的主要资料来源。这篇文章从二维旋转开始，会讨论旋转矢量、旋转矩阵、四元数、欧拉角等旋转的表示方法。在开始讨论前，需要明确的一点是刚体的姿态具有三个自由度，但使用三个参数对姿态进行全局的、没有奇异性的描述已经被证明是不可能的[2]，这也是近来IMU姿态估计的方法大多使用四元数或旋转矩阵的原因。

1. 二维旋转的表示

相比在三维空间中的旋转，二维旋转十分直观且易于理解。二维旋转指将二维平面上的一个向量

（起点为原点）绕原点旋转一个角度

，得到一个新的向量

。角度

可以完全描述这个旋转操作，因此是最直接的二维旋转的表示方法。但需要注意的是，因为角度具有周期性，任何相差

的整数倍的两个角度所代表的旋转是相同的（只考虑旋转的结果），所以表示角度的空间不是实数集

，而是一个商空间

。

这个商空间可以和平面上的单位圆做一一对应：

，也就是说，我们可以认为单位圆上的每一个点，对应了一个独特的旋转操作，这也是二维旋转的第二种表示方法。最后，如果我们把旋转后得到的向量写成坐标的形式，可以得到：

(1)

其中

被称为二维旋转矩阵，可以和

作一一对应，是二维旋转的第三种表示方法。旋转矩阵是行列式为1的正交矩阵，也就是说它的每个列向量都是单位向量，每两个列向量都是互相正交（垂直）的。

2. 旋转矢量（rotation vector）

三维旋转和二维旋转的不同是：二维旋转永远绕着垂直于平面的轴旋转，但三维旋转可以绕三维空间内的任意一根轴旋转。根据欧拉旋转定理，任何一个三维旋转可以表示为绕一根转轴

旋转一个角度

，在这里我们约定转轴

用单位向量表示。因此最直接的三维旋转的表示方法就是单位向量

和角度

，这种方法被称为欧拉轴-角（axis-angle）。为了一些计算上的方便，我们可以把轴和角相乘，得到一个三维空间内的一般向量

，很容易验证

和欧拉轴-角是一一对应的，这也就是三维旋转的另一种表示方法，即所谓的旋转矢量。需要注意的是，和二维旋转的角度表示法类似，旋转矢量也具有周期性：任何方向相同，长度相差

的整数倍（可以将负的长度理解为方向相反的向量）的两个旋转矢量表示相同的旋转。因此如果考虑独特的旋转，我们可以把旋转矢量限制在半径为

的三维球体内。

如果在三维空间内一个向量

经过旋转矢量

所表示的旋转操作后得到

，那么它们两者有以下关系（Rodrigues' rotation formula）:

(2)

最后需要说明的是，当

时，旋转矢量

的导数会出现无穷大的情况，这也是旋转矢量表示方法的奇异点。

3. 旋转矩阵（rotation matrix）

类似于二维旋转，

和

的关系也可以用矩阵的形式来表示：

(3)

其中

被称为旋转矩阵，也是 IMU 姿态表示中最常用到的方法。表示三维旋转的旋转矩阵

是一个3×3，行列式为 1 的正交矩阵，也就是说它的每个列向量都是单位向量，每两个列向量互相正交（垂直）。可以证明两个旋转矩阵的乘积还是旋转矩阵，所以全部旋转矩阵构成一个“群”，也就是著名的 SO(3) 群，其中群的乘法就是矩阵的乘法。需要注意的是，矩阵的乘法是不交换的，也就是说一般情况下

，这意味着连续进行的两个旋转如果交换顺序，那么旋转的结果也会不同。

旋转矩阵可以由旋转矢量计算得到：

(4)

其中

表示叉积矩阵，也就是对任意向量

，

，它的表达式为：

(5)

最后需要说明的是，(4)可以写成指数矩阵的表达形式：

，其中指数矩阵指：

。

4. 单位四元数（unit quaternion）

四元数是对复数数系的进一步拓展，由四个实数表示：

。三个虚数单位服从以下的运算规则：

，

，

，

。三维旋转可以用单位四元数表示，即

的四元数。四元数有以下几种常见的运算：

(i) 乘法：

(ii) 幂：

(iii) 共轭：

(iv) 逆：

对于单位四元数，它的逆运算和共轭运算的结果是一样的。需要注意的是，与旋转矩阵类似，四元数的乘法也是不交换的。

表示一个三维旋转的单位四元数可以由旋转矢量

计算得到：

(6)

将

代入上式可以得到

，这意味着

和

表示相同的三维旋转。这是单位四元数一个非常重要的性质，它和三维旋转并不是一一对应的，而是 2 比 1 的对应关系。与旋转矩阵类似，(6)也可以用指数函数的形式表示：如果将三维向量

写为一个实部为 0 的四元数

，那么

，其中四元数的指数函数为

。四元数也可以和旋转矩阵之间互相转换，具体公式可以通过欧拉轴-角表示法(4) 和 (6) 间接得到。

最后，与旋转矩阵类似，一个向量

经过单位四元数

所表示的旋转操作后，得到的

也有很简单的形式：

(7)

5. 欧拉角（Euler angles）

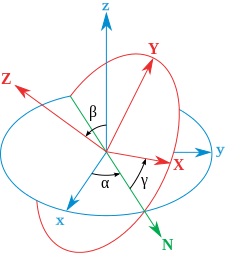
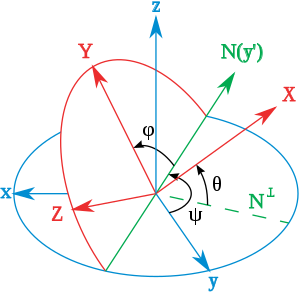
欧拉角大概是最常用到的姿态表示方法了，它的思路是把一个三维旋转分解为三个绕坐标轴的旋转。欧拉角使用时最令人困惑的地方在于它的不同定义方法：根据三个坐标轴的不同顺序，可以有12种定义方法；根据坐标轴是惯性坐标系（extrinsic）还是体坐标系（intrinsic），可以有2种定义方法。因此，一共有24种可能的方法来定义欧拉角，而且这些定义方式没有一种是通用的，因此每次使用欧拉角时一定要说明是哪种定义。在量子力学中，最常用的欧拉角是体坐标系 z-x'-z''；我个人比较喜欢的一种欧拉角是体坐标系 z-y'-x''，其中三个旋转角度也叫作yaw（航向角），pitch（俯仰角）和roll（横滚角）。

欧拉角可以很方便地转化为旋转矩阵，其中绕三个坐标轴的旋转分别可以转化为如下的旋转矩阵：

(i) 绕x轴旋转

(ii) 绕y轴旋转

(iii) 绕z轴旋转

对于用惯性坐标系定义的欧拉角，可以按坐标轴顺序将以上三个基本旋转矩阵左乘；而用体坐标系定义的欧拉角，则需按坐标轴顺序右乘。例如体坐标系 z-y'-x'' 欧拉角所对应的旋转矩阵是：

(8)

因为三维旋转具有三个自由度，所以欧拉角是所有姿态的表示方法中需要用到参数最少的一种，也就是只用到三个参数。但是这样的简化也带来了一些不方便的地方，在这里我们讨论欧拉角的两个缺点。第一个是欧拉角具有周期性，但和旋转矢量不同，它的周期性很不直观。以体坐标系 z-y'-x'' 欧拉角为例，它三个角度的范围是：

，

，

。这三个角度不仅以

为周期，而且通过

的公式可以验证：

，

，

与

，

，

表示的是相同的三维旋转。这样非常规的周期性在实践中有时难以察觉，而且也使欧拉角本身的含义变得难以理解。欧拉角的第二个缺点是“臭名昭著”的自锁现象（gimbal lock）：即当俯仰角

时，第三步中的 x-轴与第一步中的 z-轴重合，因此第一步绕 z-轴的旋转和第三步绕 x-轴的旋转实际上是一样的，导致欧拉角损失了一个自由度。在自锁点附近，横滚角

及航向角

的导数会趋向于无穷大，这也是欧拉角表示方法的奇异点。在使用卡尔曼滤波器时，这样的性质可能会使方差的计算十分不准确，我们会在后面讨论卡尔曼滤波器的文章中详细介绍这个问题。

6. 旋转和姿态的关系

在上面的讨论中，旋转矢量、旋转矩阵、四元数、欧拉角指的都是在三维空间中旋转一个向量的操作，那么这个操作和刚体的姿态有什么关系？这个问题可以用旋转矩阵回答：假设旋转矩阵

将一个坐标系 xyz 旋转到 x'y'z'（将坐标轴理解为三维向量），那么如果一个向量在 xyz 坐标系中由坐标

表示，在 x'y'z' 坐标系中由坐标

表示，这两个坐标有如下的关系：

(9)

在IMU中，我们计算的

是将一个向量在体坐标系（x'y'z'）里的坐标转为在惯性坐标系（xyz）中的坐标，那么这个旋转矩阵

的另外一层含义是将惯性坐标系旋转到体坐标系的旋转操作。

如果我们将

代入(9)可以得到：

的第一列是体坐标系的x-轴在惯性坐标系里的坐标；类似的，

的第二、三列分别是体坐标系的 y-轴和 z-轴在惯性坐标系里的坐标。因为的

逆和它的转置相等，所以

的第一、二、三行分别是惯性坐标系的 x-轴、y-轴、z-轴在体坐标系里的坐标。

7. 总结

刚体的姿态一般可以用四种方法表示：旋转矢量、旋转矩阵、四元数和欧拉角。刚体的姿态有三个自由度，在四种表示方法中，旋转矢量和欧拉角用了三个参数；四元数用了四个参数和一个约束条件（长度为1）；旋转矩阵用了九个参数和六个约束条件（矩阵的正交性）。旋转矢量和欧拉角都具有奇异性，也就是说在某种姿态下，它们的导数会趋向无穷大；四元数没有奇异性，但它和姿态是2比1的对应关系；只有旋转矩阵既没有奇异性，而且和姿态是一一对应的。在IMU姿态估计中，可以使用旋转矩阵、四元数或欧拉角对角速度进行积分，并设计滤波器。在乘法扩展卡尔曼滤波器中（MEKF），是用四元数进行积分，用旋转矢量表示姿态误差及估计姿态的协方差矩阵。