Unity中的矩阵（Matrix4x4）

最近在研究帧同步定点数物理系统中需要自定义定点数矩阵，所以在这里分享下基础的矩阵案例旋转、平移、缩放。（注意这里本文中的transform组件式基于unity浮点数的教程并非帧同步定点数）参考原文

创建自定义模型

参数可以参考我上图的参数，这里注意三个顶点是一个面，这里我上述的模型是一个三角形的面。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;public class Triangle : MonoBehaviour
{/// <summary>/// 网格/// </summary>Mesh mesh;/// <summary>/// 三角形顶点/// </summary>public Vector3[] vertices;/// <summary>/// 分配三角形顶点索引/// </summary>public int[] triangle;/// <summary>/// 材质球/// </summary>public Material mat;private void Start(){//实例化网格mesh = new Mesh();//分配顶点mesh.vertices = vertices;//分配三角形顶点索引mesh.triangles = triangle;//添加网格过滤器MeshFilter mf = gameObject.AddComponent<MeshFilter>();//网格赋值mf.mesh = mesh;//添加网格渲染器MeshRenderer mr = gameObject.AddComponent<MeshRenderer>();//材质赋值mr.materials[0] = mat;}
}

创建模型很简单我就不细讲了，看不懂的可以看上述的注释即可，直接黏贴也可。

平移矩阵

要做位移先搞明白矩阵中的哪几个索引值代表的坐标位置，如下图所示4x4矩阵

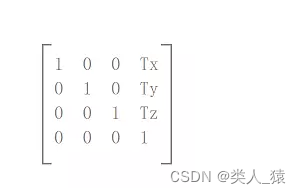
上图Tx，Ty，Tz为平邑的方向向量

这里可以自己做个测试，将transform的初始位置修改如下所示

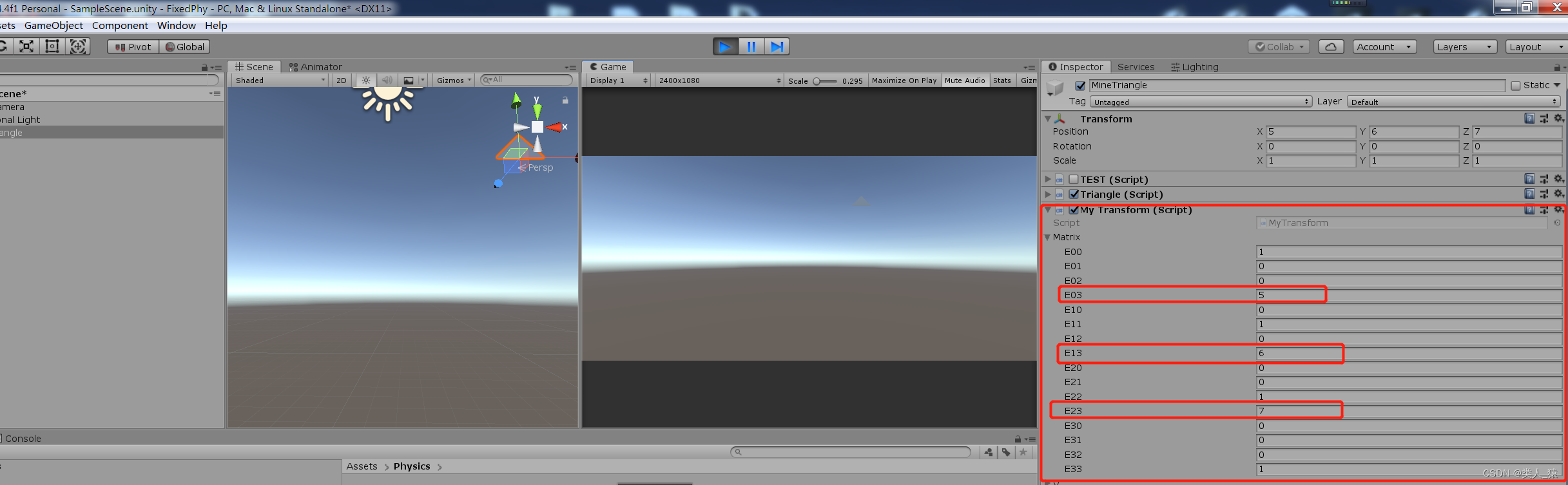
代码如下

using System.Collections;
using System.Collections.Generic;
using UnityEngine;public class MyTransform : MonoBehaviour
{public Matrix4x4 matrix;// Start is called before the first frame updatevoid Start(){matrix.SetTRS(transform.position,transform.rotation,transform.localScale);}// Update is called once per framevoid Update(){if (Input.GetKeyDown(KeyCode.Q)) {MyTranslate(new Vector3 (Random.Range(-5,5),Random.Range(-5,5), Random.Range(-5, 5)));}}public Vector4 v;/// <summary>/// 平移矩阵对象/// </summary>/// <param name="pos"></param>public void MyTranslate(Vector3 pos) {//按照当前位置进行位移//v = new Vector4(transform.position.x,transform.position.y,transform.position.z,1);//按照原点进行位移v = new Vector4(0, 0, 0, 1);matrix = Matrix4x4.identity;//X、Y、Z移动因子matrix.m03 = pos.x;matrix.m13 = pos.y;matrix.m23 = pos.z;//矩阵位移操作v = matrix * v;transform.position = new Vector3(v.x, v.y, v.z);}
}

缩放矩阵

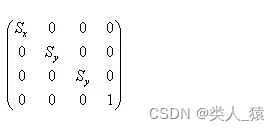
这个就是缩放矩阵，其中“Sx”、“Sy”、“Sz”就是各个轴上的缩放因子。缩放矩阵是矩阵表现物体大小变换的矩阵。如果缩放因子小于1，表现为物体缩小；如果大于1，则表现为物体扩大，如果等于1则不发生变化。

测试的话可以根据平移矩阵的测试方式修改scale来查看矩阵点对应值得变化

修改代码如下

using System.Collections;
using System.Collections.Generic;
using UnityEngine;public class MyTransform : MonoBehaviour
{public Matrix4x4 matrix;// Start is called before the first frame updatevoid Start(){matrix.SetTRS(transform.position,transform.rotation,transform.localScale);}// Update is called once per framevoid Update(){if (Input.GetKeyDown(KeyCode.Q)) {MyTranslate(new Vector3 (Random.Range(-5,5),Random.Range(-5,5), Random.Range(-5, 5)));}if (Input.GetKeyDown(KeyCode.W)) {int scale = Random.Range(-5,5);MyScale(new Vector3 (scale, scale, scale));}}public Vector4 v;/// <summary>/// 平移矩阵对象/// </summary>/// <param name="pos"></param>public void MyTranslate(Vector3 pos) {//按照当前位置进行位移//v = new Vector4(transform.position.x,transform.position.y,transform.position.z,1);//按照原点进行位移v = new Vector4(0, 0, 0, 1);matrix = Matrix4x4.identity;//X、Y、Z移动因子matrix.m03 = pos.x;matrix.m13 = pos.y;matrix.m23 = pos.z;//矩阵位移操作v = matrix * v;transform.position = new Vector3(v.x, v.y, v.z);}/// <summary>/// 缩放矩阵对象/// </summary>/// <param name="scale"></param>public void MyScale(Vector3 scale) {//设置当前对象大小//v = new Vector4(transform.localScale.x, transform.localScale.y, transform.localScale.z, 1);//按照原点进行位移v = new Vector4(1, 1, 1, 1);matrix = Matrix4x4.identity;//X、Y、Z缩放因子matrix.m00 = scale.x;matrix.m11 = scale.y;matrix.m22 = scale.z;//矩阵缩放操作v = matrix * v;transform.localScale = new Vector3(v.x, v.y, v.z);}
}

旋转矩阵

测试的话可以根据平移矩阵的测试方式修改Rotation来查看矩阵点对应值得变化

修改代码如下

using System.Collections;
using System.Collections.Generic;
using UnityEngine;public class MyTransform : MonoBehaviour
{public Matrix4x4 matrix;// Start is called before the first frame updatevoid Start(){matrix.SetTRS(transform.position,transform.rotation,transform.localScale);}// Update is called once per framevoid Update(){if (Input.GetKeyDown(KeyCode.Q)) {MyTranslate(new Vector3 (Random.Range(-5,5),Random.Range(-5,5), Random.Range(-5, 5)));}if (Input.GetKeyDown(KeyCode.W)) {int scale = Random.Range(-5,5);MyScale(new Vector3 (scale, scale, scale));}if (Input.GetKeyDown(KeyCode.A)) {MyRotation( Axle.X,10f);}if (Input.GetKeyDown(KeyCode.S)){MyRotation(Axle.Y, 10f);}if (Input.GetKeyDown(KeyCode.D)){MyRotation(Axle.Z, 10f);}}public Vector4 v;/// <summary>/// 平移矩阵对象/// </summary>/// <param name="pos"></param>public void MyTranslate(Vector3 pos) {//按照当前位置进行位移//v = new Vector4(transform.position.x,transform.position.y,transform.position.z,1);//按照原点进行位移v = new Vector4(0, 0, 0, 1);matrix = Matrix4x4.identity;//X、Y、Z移动因子matrix.m03 = pos.x;matrix.m13 = pos.y;matrix.m23 = pos.z;//矩阵位移操作v = matrix * v;transform.position = new Vector3(v.x, v.y, v.z);}/// <summary>/// 缩放矩阵对象/// </summary>/// <param name="scale"></param>public void MyScale(Vector3 scale) {//设置当前对象大小//v = new Vector4(transform.localScale.x, transform.localScale.y, transform.localScale.z, 1);//按照原点进行位移v = new Vector4(1, 1, 1, 1);matrix = Matrix4x4.identity;//X、Y、Z缩放因子matrix.m00 = scale.x;matrix.m11 = scale.y;matrix.m22 = scale.z;//矩阵缩放操作v = matrix * v;transform.localScale = new Vector3(v.x, v.y, v.z);}public enum Axle { X, Y, Z}public void MyRotation(Axle axle,float angle) {matrix = Matrix4x4.identity;//对应 X、Y、Z的旋转switch (axle){case Axle.X:matrix.m11 = Mathf.Cos(angle * Mathf.Deg2Rad);matrix.m12 = -Mathf.Sin(angle * Mathf.Deg2Rad);matrix.m21 = Mathf.Sin(angle * Mathf.Deg2Rad);matrix.m22 = Mathf.Cos(angle * Mathf.Deg2Rad);break;case Axle.Y:matrix.m00 = Mathf.Cos(angle * Mathf.Deg2Rad);matrix.m02 = Mathf.Sin(angle * Mathf.Deg2Rad);matrix.m20 = -Mathf.Sin(angle * Mathf.Deg2Rad);matrix.m22 = Mathf.Cos(angle * Mathf.Deg2Rad);break;case Axle.Z:matrix.m00 = Mathf.Cos(angle * Mathf.Deg2Rad);matrix.m01 = -Mathf.Sin(angle * Mathf.Deg2Rad);matrix.m10 = Mathf.Sin(angle * Mathf.Deg2Rad);matrix.m11 = Mathf.Cos(angle * Mathf.Deg2Rad);break;default:break;}float qw = Mathf.Sqrt(1f + matrix.m00 + matrix.m11 + matrix.m22) / 2;float w = 4 * qw;float qx = (matrix.m21 - matrix.m12) / w;float qy = (matrix.m02 - matrix.m20) / w;float qz = (matrix.m10 - matrix.m01) / w;transform.rotation = new Quaternion(qx, qy, qz, qw);}}

原文中有对应的小工具可以参考