一、项目简介

本项目主要基于SpringBoot、Mybatis-plus、MySQL、Redis实现的书店管理系统。
本系统是前后端分离的，分别由三个子项目构成：java服务端、用户浏览与购买的前端、管理员管理商品的前端

环境

• java 1.8
• mysql8.0
• redis
• vue2.x

管理员子系统功能

• 商品创建与编辑
• 商品上下架
• 订单管理，查看下单情况
• 订单管理，查看订单详情
• 轮播图管理，维护用户端上方的轮播图广告

用户端子系统功能

• 用户注册与登录
• 首页轮播图广告
• 首页热门商品
• 全部商品
• 商品搜索
• 商品加入购物车
• 提交购买订单
• 付款（点击就表示付款了哈哈哈哈哈）
• 订单详情查看
• 收货地址管理
• 密码修改

二、运行展示

用户端

首页

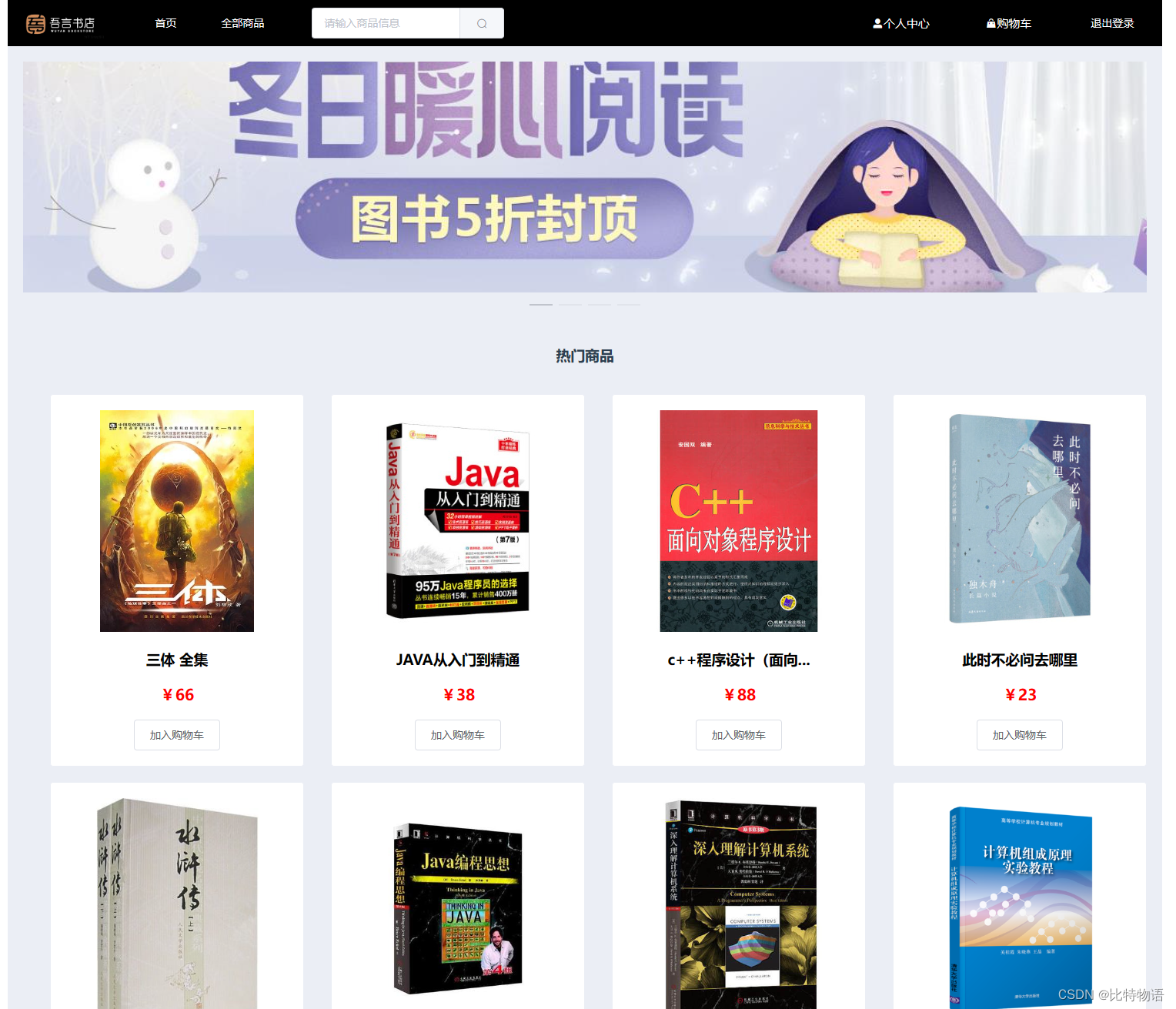
全部商品

商品详情

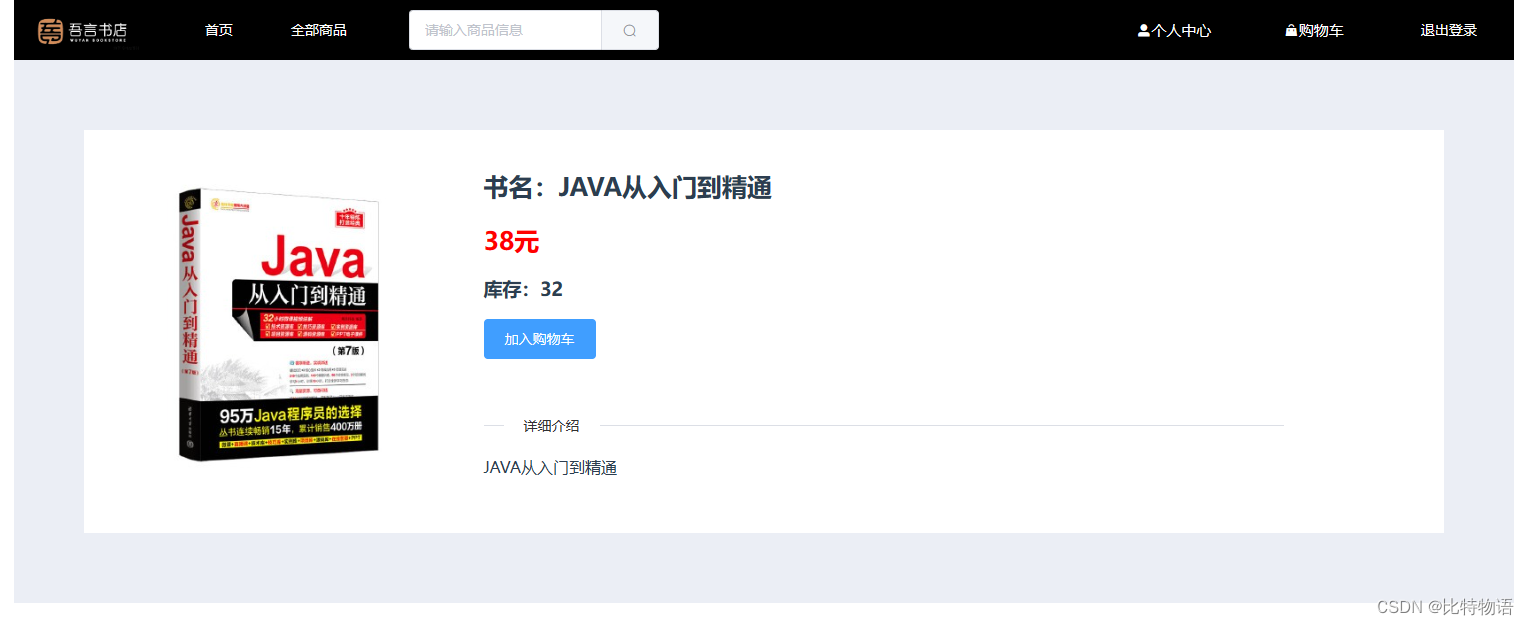
购物车

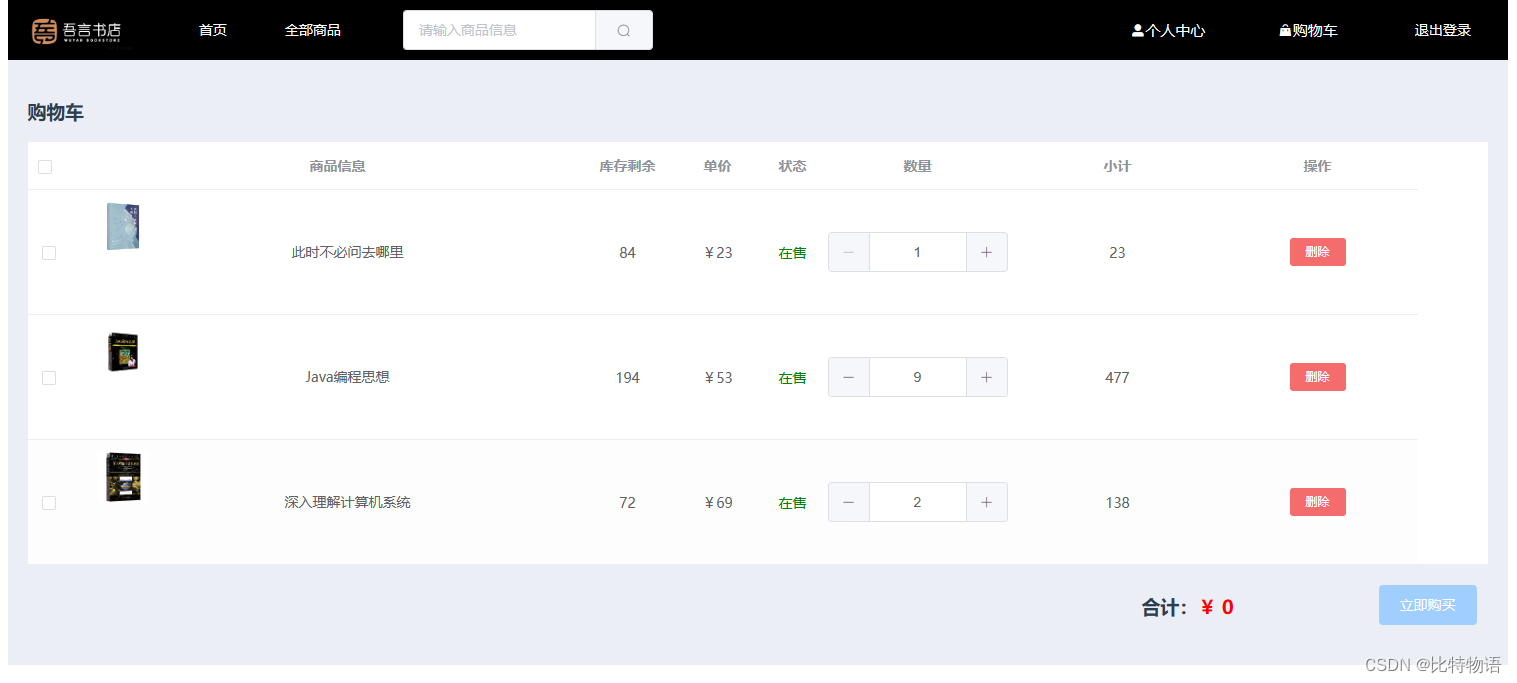
订单中心

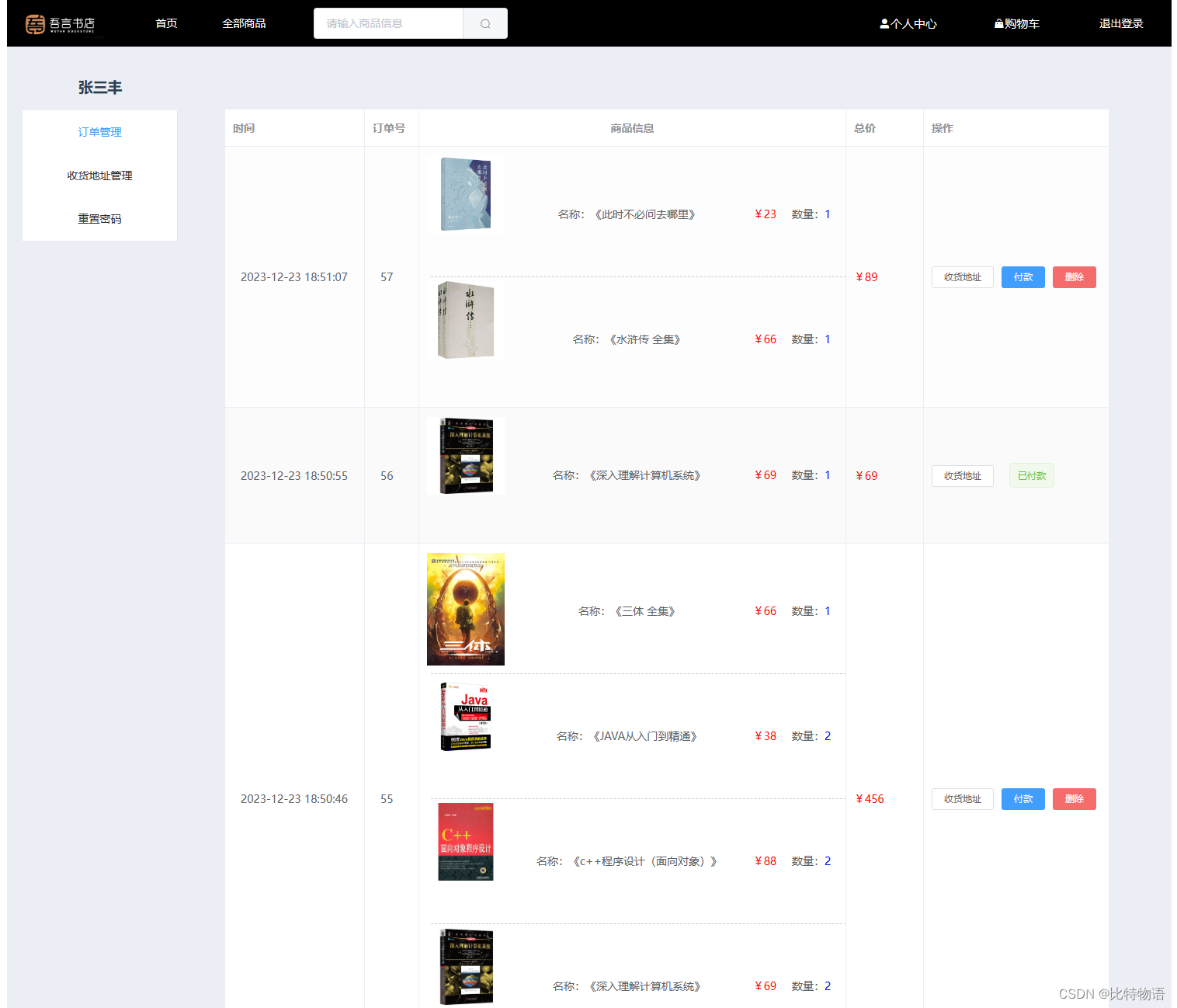
收货地址

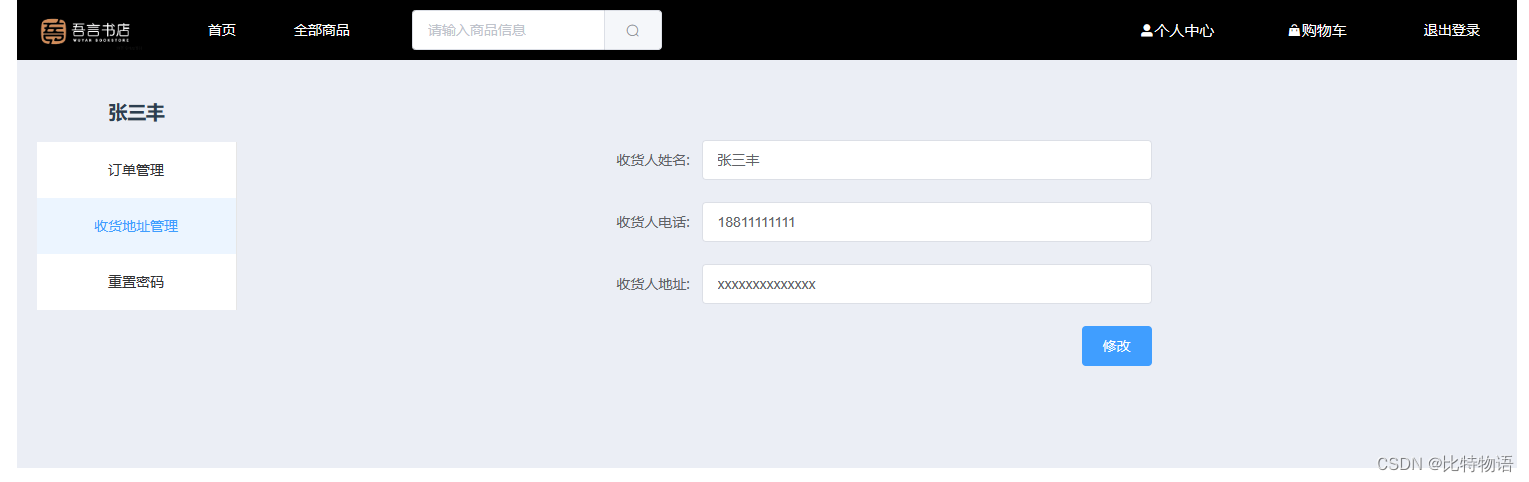
管理员端

商品管理

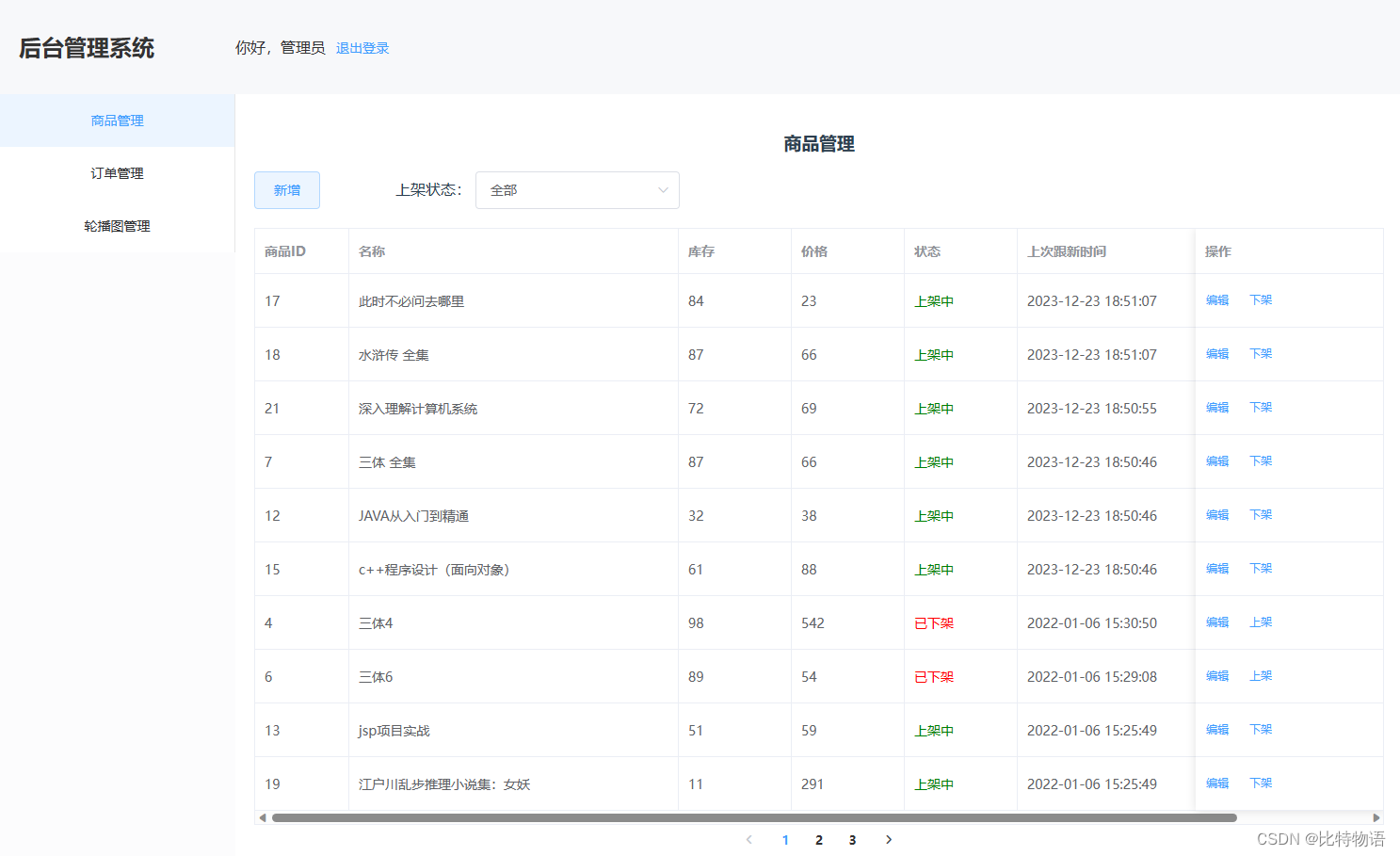
商品编辑

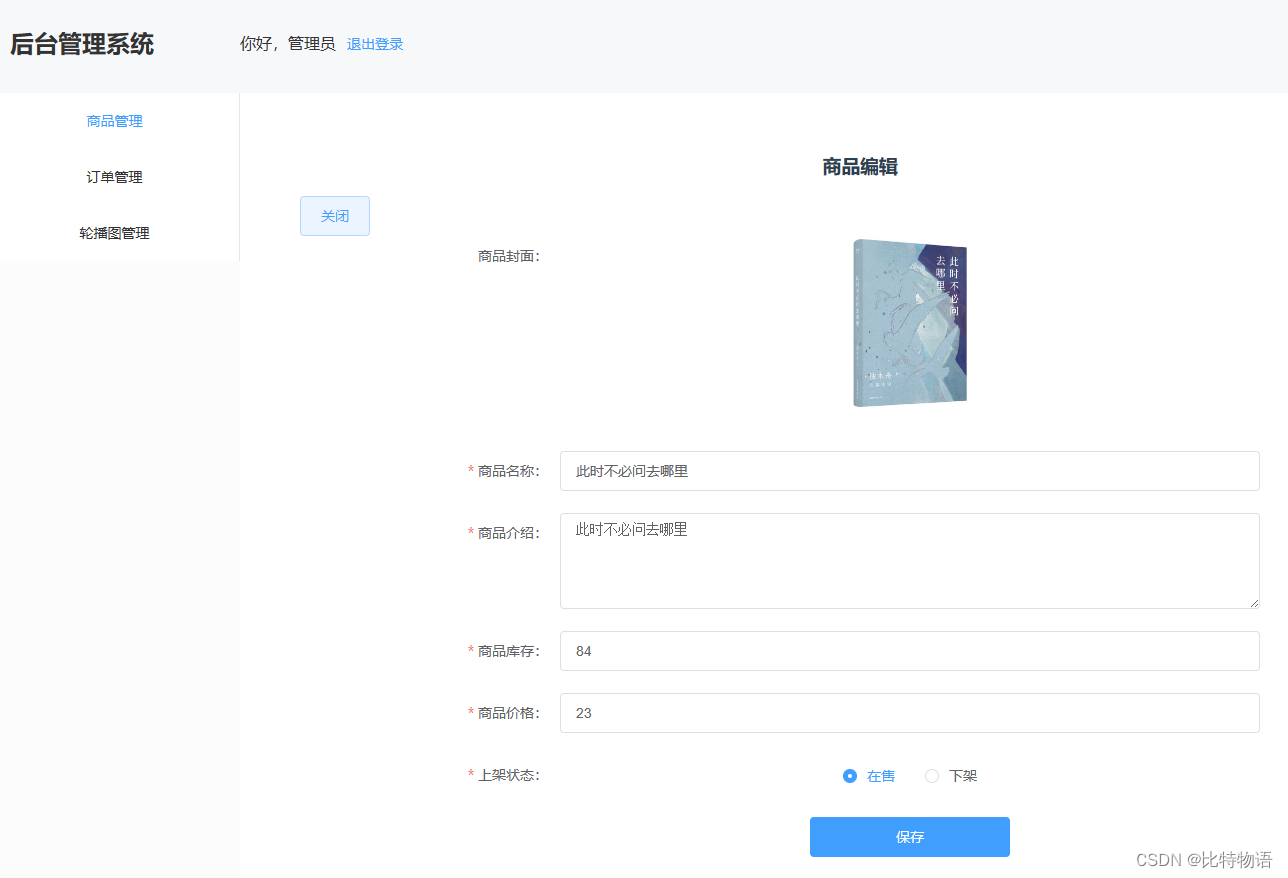
订单管理

订单详情

轮播图管理

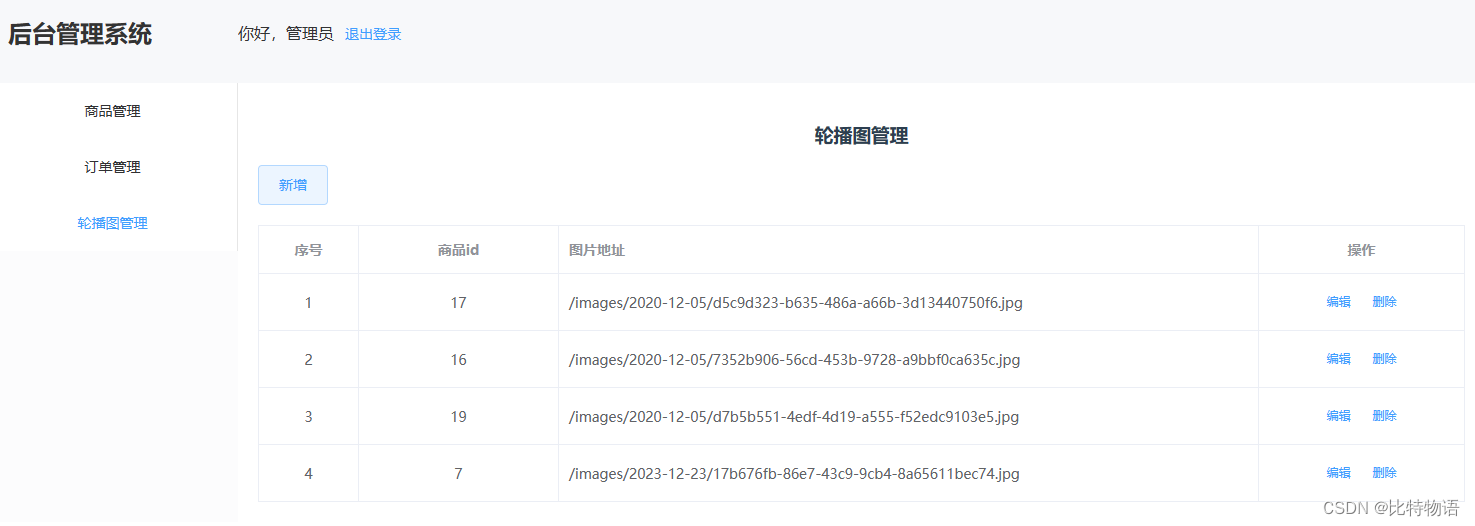
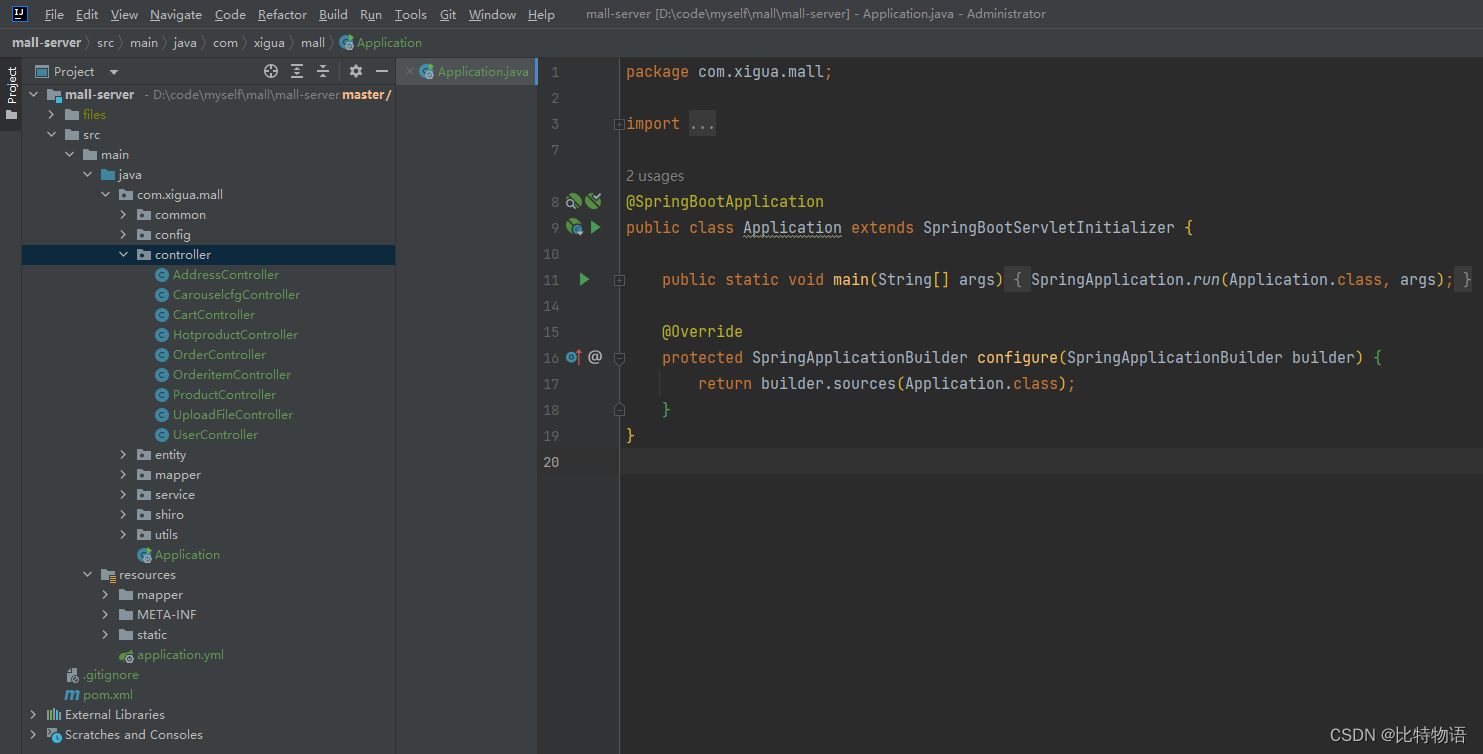
java端项目结构

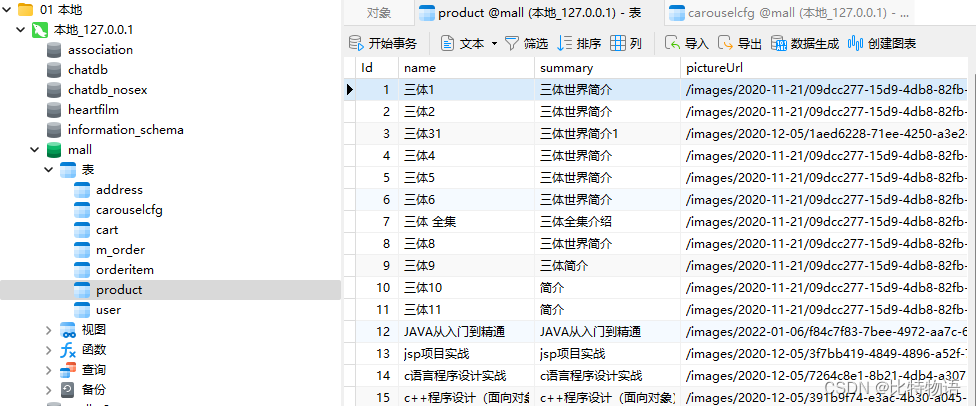
数据库结构