背包问题

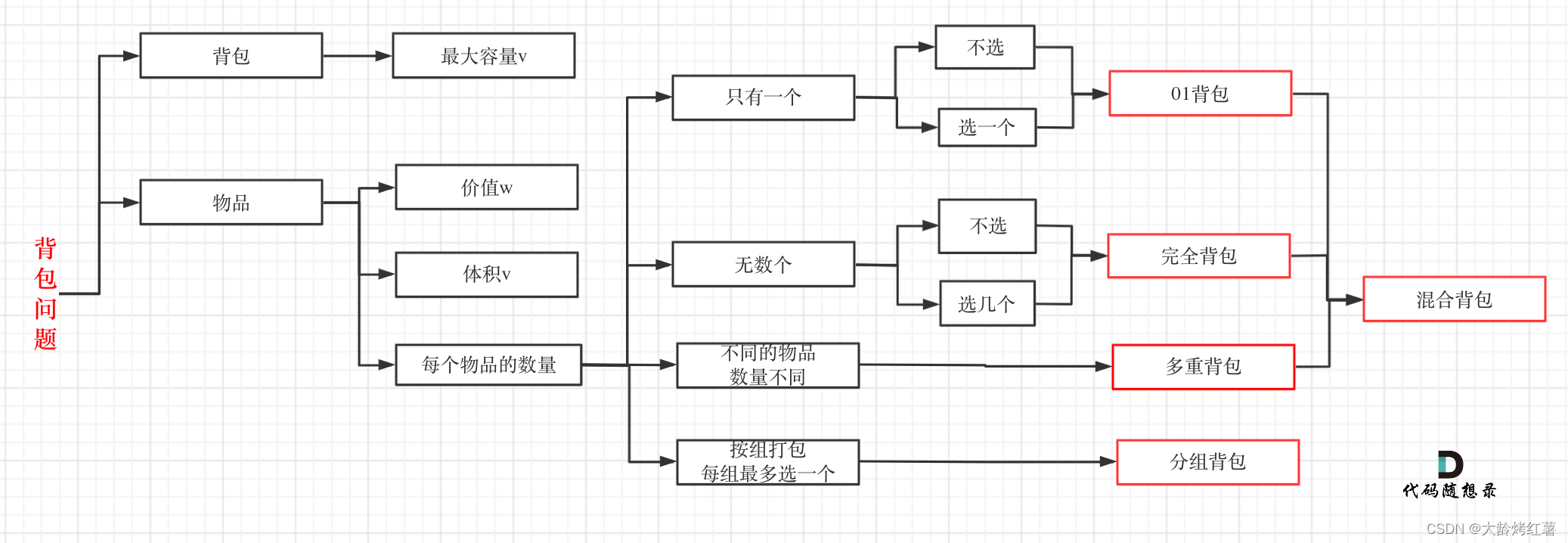
动规五部曲

其中最主要的就是前两个步骤

• 确定dp数组以及下标的含义
• 确定递推公式
• dp数组如何初始化
• 遍历顺序
• 出结论，写代码

一、0-1背包问题 ：限制物品不可重复 (要么不选 要么选一个)

二、完全背包问题：不限制重复（要么不选 要么可以多选）（完全背包可以转化为0-1背包问题）

下面讲的是0-1背包问题：

其中：

• i,表示物品；j表示背包容量；
• w[] 数组表示物品重量的集合；
• v[] 数组表示物品价值的集合；
• v[][]表示装入背包的最大价值集合；

（1）找w[i]和j的关系

v[i][0]=v[0][j]=0,表示第一列和第一行最大价值都是0；

• 1.w[i]>j,表示当前准备新增物品的质量要是大于背包的容量，v[i][j] =v[i-1][j]，该位置的最大价值就是把该列上一行的数据赋给它；如第二次音响进来的最大价值情况；v[i-1][j]上一个单元格装入的最大价值；
• 2.j>=w[i]，表示背包的容量要是大于等于当前要新增物品的质量；

(2) 则装入的最大价值策略为：v[i][j] = max { v[i-1][j], v[i] + v[i-1][j-w[i]] }
v[i] 当前商品的价值；
j-w[i] 装入当前物品后，背包剩余的容量大小；

(3) v[i] + v[i-1][j-w[i]]表示：装入当前物品的价值 + 剩余容量可装入的最大价值
最后比较 两个最大价值，取max

eg：总w=4；电脑w=3装入后的价值2000 + 剩余w=1只可装一个吉他价值1500=3500 > 上一个单元格装入的最大价值3000
所以选择这个装配方式；

上面讲的很清楚了 看一下具体的实现

那么可以有两个方向推出来dp[i][j]：

1.不放物品i：dp[i][j]=dp[i - 1][j]。
w[i]>j，表示：当前准备新增物品的质量要是大于背包的容量，v[i][j] =v[i-1][j]，
就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。

2.放物品i：
表示背包的容量要是大于等于当前要新增物品的质量；

• dp[i - 1][j - weight[i]]推出，
  dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候 不放物品i（所以是i-1）的最大价值
• value[i]+dp[i - 1][j - weight[i]]
  表示：装入当前物品的价值 + 剩余容量可装入的最大价值

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

动态规划：01背包 二维dp数组

动规五部曲分析一波。

1. 确定dp数组以及下标的含义

- 对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0,i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
- w[i] 表示第i个物品的重量；
- v[i] 表示第i个物品的价值；

要时刻记着这个dp数组的含义，下面的一些步骤都围绕这dp数组的含义进行的，如果哪里看懵了，就来回顾一下i代表什么，j又代表什么。

2. 确定递推公式

再回顾一下dp [i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

# 那么可以有两个方向推出来dp[i][j]：
##1.不放物品i：dp[i][j]=dp[i - 1][j]。
------w[i]>j,表示当前准备新增物品的质量要是大于背包的容量，v[i][j] =v[i-1][j]，就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。
##2.放物品i：表示背包的容量要是大于等于当前要新增物品的质量；#  dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候 不放物品i（所以是i-1）的最大价值，#  value[i]+dp[i - 1][j - weight[i]]  表示：装入当前物品的价值 + 剩余容量可装入的最大价值所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

动态规划：01背包滚动数组

读到这里估计大家都忘了 dp[i][j]里的i和j表达的是什么了，i是物品，j是背包容量。

dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

动规五部曲分析如下：

1. 确定dp数组的定义

   在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。

2. 一维dp数组的递推公式

• dp[j]可以通过dp[j - weight[i]]推导出来：
  dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
  dp[j - weight[i]] + value[i] 表示：容量为 j-物品i重量的背包的价值 加上 物品i的价值。
  （就是容量为j的背包，放入物品i了之后的价值再加上物品i的价值）
• 此时dp[j]有两个选择：
  一个是取自己dp[j] 相当于二维dp数组中的dp[i-1][j]，即不放物品i；
  一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值，
• 所以递归公式为：
  dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

3. 一维dp数组如何初始化

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么背包容量为0所背的物品的最大价值就是0。

所以dp[0]=0；

假设物品价值都是大于0的，所以dp数组初始化的时候，都初始为0就可以了。

Arrays.fill(dp,0);

4. 遍历顺序从后向前

​ 还是先遍历物品，然后再遍历背包容量

for(int i = 0; i < v.length; i++) { // 遍历物品for(int j = weight; j >= w[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - w[i]] + v[i]);}
}

动态规划代码

5. 代码

public static void main(String[] args) {int[] v = {15, 20, 30};int[] w = {1, 3, 4};int weight = 4;int[] dp = new int[weight + 1];Arrays.fill(dp, 0);//i是物品 j是背包重量 所以物品重量是w[i]int res=dp[0];for (int i = 0; i < v.length; i++) {for (int j = weight; j >= w[i]; j--) {dp[j]=Math.max(dp[j],dp[j-w[i]]+v[i]);res=Math.max(res,dp[j]);}}System.out.println(res);}

public static void main(String[] args) {int[] value = new int[]{1500, 2000, 3000};//表示物品的价值int[] weight = {1, 4, 3};//表示物品的重量int w = 4;//背包的容量int n = value.length;//物品的个数//创建一个二维数组 表 n+1行：有一行是0行；w+1列：有一列是0列int[][] dp = new int[n + 1][w + 1];  //n+1就是列长 w+1就是行长//1.初始化第一行第一列for (int i = 0; i < w + 1; i++) {dp[0][i] = 0;//第一行为0}for (int i = 0; i < n + 1; i++) {dp[i][0] = 0;//第一列为0}int res=dp[0][0];//2.判断物品重量w[i] 和背包容量的关系for (int i = 1; i < dp.length; i++) {//从第一行for (int j = 1; j < dp[0].length; j++) {//第一列开始if (weight[i-1] > j) {//i-1是因为我们从1开始的dp[i][j] = dp[i - 1][j];} else {dp[i][j] = Math.max(dp[i - 1][j], (value[i-1] + dp[i - 1][j - weight[i-1]]));//value[i-1] //是因为我们的i是从1开始的 所以-1//weight[i-1]}res=Math.max(res,dp[i][j]);}}
//        3.打印这个最大价值表for (int i = 0; i <dp.length ; i++) {for (int j = 0; j <dp[0].length; j++) {System.out.print(dp[i][j]+"\t");}System.out.println();}System.out.println("最大价值为："+res);}
}