738. 单调递增的数字 - 力扣(LeetCode)
这个问题是关于找到一个小于或等于给定数字n的最大单调递增数字。
我们可以将数字n转换为字符数组,然后从左到右扫描,寻找第一个违反单调递增条件的位置。一旦找到这样的位置,我们将该位置上的数字减一,并将其右侧的所有数字设置为9,以使得整个数字尽可能大。
然而,这个策略可能会导致左侧的一些数字违反单调递增的条件,因此我们需要从违反位置开始向左扫描,以确保整个数字仍然是单调递增的。
以下是解决问题的Python代码:
def monotoneIncreasingDigits(n: int) -> int:digits = list(str(n))n = len(digits)pos = n # 用来记录第一个违反单调递增条件的位置# 扫描从左到右找到第一个违反单调递增条件的位置for i in range(n - 1, 0, -1):if digits[i] < digits[i - 1]:pos = idigits[i - 1] = str(int(digits[i - 1]) - 1)# 将pos右侧的所有数字设置为9for i in range(pos, n):digits[i] = '9'return int(''.join(digits))
我们可以用给定的示例来测试这个函数:
print(monotoneIncreasingDigits(10)) # 输出: 9
print(monotoneIncreasingDigits(1234)) # 输出: 1234
print(monotoneIncreasingDigits(332)) # 输出: 299
注:这题的关键还是通过样例观察规律,找到贪心的解法
968. 监控二叉树 - 力扣(LeetCode)
使用贪心算法来解决此问题的关键思想是自底向上遍历二叉树,并尽可能地在没有摄像头的父节点上放置摄像头。以下是具体步骤和实现:
- 我们可以自底向上遍历二叉树,使用后序遍历。
- 为了记录每个节点的状态,我们可以使用三个常量表示:0表示未监视,1表示有摄像头,2表示被监视。
- 如果任何子节点未监视,则在当前节点放置摄像头。
- 如果任何子节点有摄像头,则当前节点被监视。
- 如果所有子节点都被监视,则当前节点未监视。
- 我们需要确保根节点被监视,所以如果根节点未监视,则增加一个摄像头。
以下是Python代码实现:
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef minCameraCover(root: TreeNode) -> int:NOT_MONITORED, MONITORED_WITHOUT_CAM, MONITORED_WITH_CAM = 0, 1, 2cameras = 0# 后序遍历函数def dfs(node):nonlocal camerasif not node:return MONITORED_WITHOUT_CAMleft = dfs(node.left)right = dfs(node.right)if left == NOT_MONITORED or right == NOT_MONITORED:cameras += 1return MONITORED_WITH_CAMif left == MONITORED_WITH_CAM or right == MONITORED_WITH_CAM:return MONITORED_WITHOUT_CAMreturn NOT_MONITORED# 如果根节点未监视,则增加一个摄像头if dfs(root) == NOT_MONITORED:cameras += 1return cameras
可以使用上面给出的示例来测试该函数,结果应与之前相同。这种贪心策略确保了在满足所有约束的情况下使用的摄像头数量最少。
贪心算法总结
如果找出局部最优并可以推出全局最优,就是贪心,如果局部最优都没找出来,就不是贪心,可能是单纯的模拟。
在做贪心题的过程中,如果再来一个数据证明,其实没有必要,手动模拟一下,如果找不出反例,就试试贪心。面试中,代码写出来跑过测试用例即可,或者自己能自圆其说理由就行了
星友总结的思维导图如下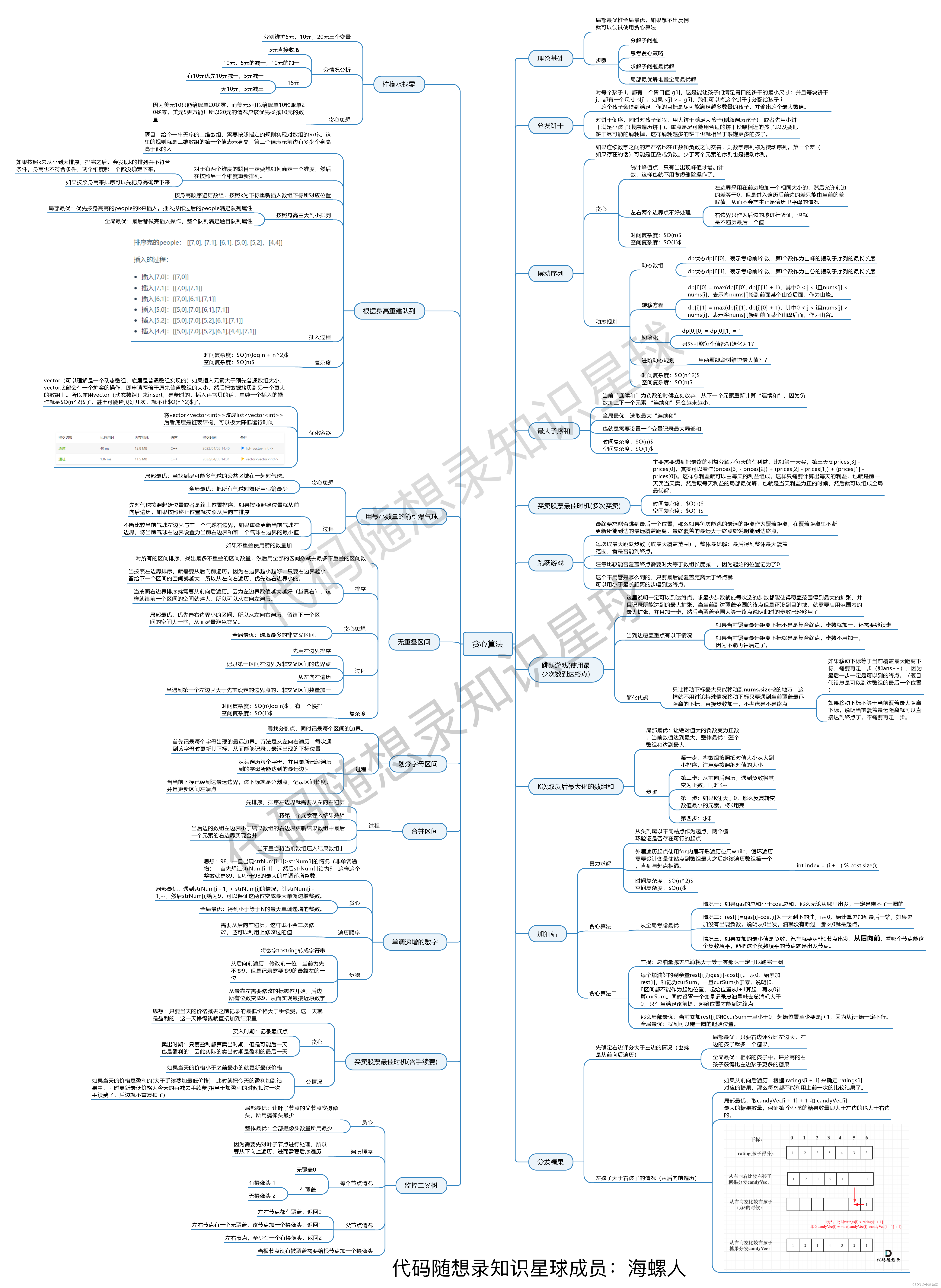












 的 fftshift, ifftshift 函数的实现)
——物联网之Blynk 2)

)



