文章目录
- 引言
- 和为 K 的子数组
- 题目描述
- 提示
- 解决方案1:【暴力枚举】
- 解决方案2:【前缀和】
- 结束语
和为 K 的子数组
引言
编写通过所有测试案例的代码并不简单,通常需要深思熟虑和理性分析。虽然这些代码能够通过所有的测试案例,但如果不了解代码背后的思考过程,那么这些代码可能并不容易被理解和接受。我编写刷题笔记的初衷,是希望能够与读者们分享一个完整的代码是如何在逐步的理性思考下形成的。我非常欢迎读者的批评和指正,因为我知道我的观点可能并不完全正确,您的反馈将帮助我不断进步。如果我的笔记能给您带来哪怕是一点点的启示,我也会感到非常荣幸。同时,我也希望我的分享能够激发您的灵感和思考,让我们一起在编程的道路上不断前行~
和为 K 的子数组
题目描述
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
- 子数组:是数组中元素的连续非空序列。
示例 1:
- 输入:nums = [1,1,1], k = 2
- 输出:2
示例 2:
- 输入:nums = [1,2,3], k = 3
- 输出:2
提示
- 1 <= nums.length <= 2 * 104
- 1000 <= nums[i] <= 1000
- 107<= k <= 107
解决方案1:【暴力枚举】
根据题意,我们需要统计数组nums中和为k的子数组的个数。为了做到这一点,一种直接方法是遍历所有子数组,然后检查每个子数组的和是否等于k。
完整代码如下:
class Solution: def subarraySum(self, nums: List[int], k: int) -> int: # 初始化计数器为0 count = 0 # 获取数组的长度 n = len(nums) # 遍历数组 for i in range(n): # 初始化tmp_sum为0 tmp_sum = 0 # 遍历当前元素之后的数组 for j in range(i, n): # 累加当前元素到tmp_sum tmp_sum += nums[j] # 如果tmp_sum等于k,则计数器加1 if tmp_sum == k: count += 1 # 返回最终的计数结果 return count
运行结果:
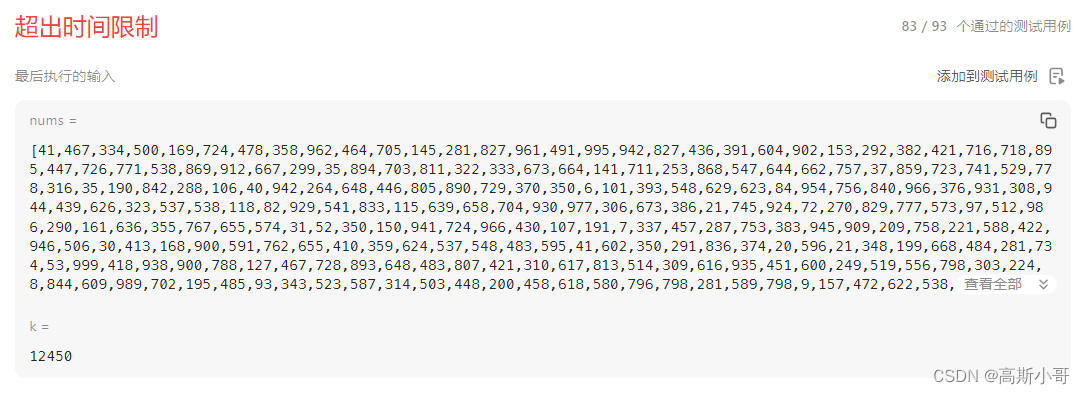
虽然这种方法很直接,但它的效率并不高,因为它涉及到两层循环的暴力枚举,时间复杂度为O(n2), 不能通过所有的测试用例。
问题1:从运行结果来看,暴力枚举算法应该存在巨大的优化空间,代码哪些部分可以进一步优化呢?
暴力枚举算法简单粗暴,如果能够优化,一定是在两层遍历中找到优化点! ⇒ 拆解for循环,尝试找到优化点
我们将sum(i --> j)定义为子数组nums[i: j+1]的和(即包括位置j)
- 当
i=0时,tmp_sum可以动态记录sum(0 --> j),其中j从0—>n-1 - 当
i为区间[1, n-1]的任意值时,tmp_sum可以动态记录sum(i --> j),其中j从i—>n-1。 对于任意的j,sum(i --> j)等价于sum(0 --> j)-sum(0 --> i-1),更关键的是,sum(0 --> j)和sum(0 --> i-1)已经在i=0时就已经计算出来了 ⇒ 只需要知道所有的sum(0 --> j),其中j从0—>n-1,就可以算出任意区间[i, j]的子数组和sum(i --> j)!!!
问题2:通过拆解for循环,我们知道用好sum(0 --> j)是进一步优化算法的关键,那么基于sum(0 --> j)的算法有没有约定俗成的名称?
有,[sum(0 --> j), for j in range(n)]实际上就是数组nums的前缀和数组!
解决方案2:【前缀和】
问题3:现在我们已知前缀和数组[sum(0 --> j), for j in range(n)],如何找到满足和为k的所有子数组呢?
首先,明确核心目标:找到所有满足和为k的所有子数组的个数。
当遍历到nums的第i个元素时,我们已知
-
sum(0 --> j), j从0 --> i的所有情况 ; - 区间[0, i]内的任意以i为终止位置的子区间[j ,i]的和都可以通过
sum(0 --> i) - sum(0 --> j)获取;
那么对于以i为终止位置的任意子区间[j ,i],只要sum(0 --> i) - sum(0 --> j) = k成立,那么都是我们要找的子数组。如果我们提前用字典数据结构pre_sum_dict存储所有出现过的前缀和,以和为键,以和出现的次数为值 ⇒ 查找sum(0 --> i) - k 是否存在于 pre_sum_dict, 若存在,且pre_sum_dict[sum(0 --> i) - k]的值为N ⇒ 找到了N个以i为终止位置的子区间[j ,i],满足sum(0 --> i) - sum(0 --> j) = k。
通过一次for循环,i从0取到n-1,我们就可以得到每个循环下所有以i为终止位置且满足和为k的子数组个数,用count作为计数器进行计数即可得到满足和为k的所有子数组的个数。
完整代码如下:
class Solution: def subarraySum(self, nums: List[int], k: int) -> int: # 初始化计数器为0 count = 0 # 获取数组的长度 n = len(nums) # 创建一个字典用于存储前缀和及其出现的次数 pre_sum_dict = {} # 初始化前缀和为0的次数为1 pre_sum_dict[0] = 1 # 初始化前缀和为0 cur_pre_sum = 0 # 遍历数组 for i in range(n): cur_pre_sum += nums[i] # 以i为结束位置的数组nums[:i+1]的和# 如果前缀和减去目标值在之前的前缀和中出现过 if cur_pre_sum - k in pre_sum_dict: # 将出现次数加入计数器 count += pre_sum_dict[cur_pre_sum - k] # 如果前缀和不在之前的前缀和中出现过 if cur_pre_sum not in pre_sum_dict: # 将前缀和加入字典并设置出现次数为1 pre_sum_dict[cur_pre_sum] = 1 else: # 否则将前缀和的出现次数加1 pre_sum_dict[cur_pre_sum] += 1 return count
运行结果:

复杂度分析
- 时间复杂度:O(n), n为数组nums的元素个数。
- 空间复杂度:O(n),哈希字典需要存放n个前缀和。
结束语
- 亲爱的读者,感谢您花时间阅读我们的博客。我们非常重视您的反馈和意见,因此在这里鼓励您对我们的博客进行评论。
- 您的建议和看法对我们来说非常重要,这有助于我们更好地了解您的需求,并提供更高质量的内容和服务。
- 无论您是喜欢我们的博客还是对其有任何疑问或建议,我们都非常期待您的留言。让我们一起互动,共同进步!谢谢您的支持和参与!
- 我会坚持不懈地创作,并持续优化博文质量,为您提供更好的阅读体验。
- 谢谢您的阅读!
:数据库主从同步的原理)

)
















