前言:前面我们学习了堆的模拟实现,今天我们来进一步学习二叉树,当然了内容肯定是越来越难的,各位我们一起努力!
💖 博主CSDN主页:卫卫卫的个人主页 💞
👉 专栏分类:数据结构 👈
💯代码仓库:卫卫周大胖的学习日记💫
💪关注博主和博主一起学习!一起努力!
什么是树
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。光看文字可能大家理解不了,我们看下图。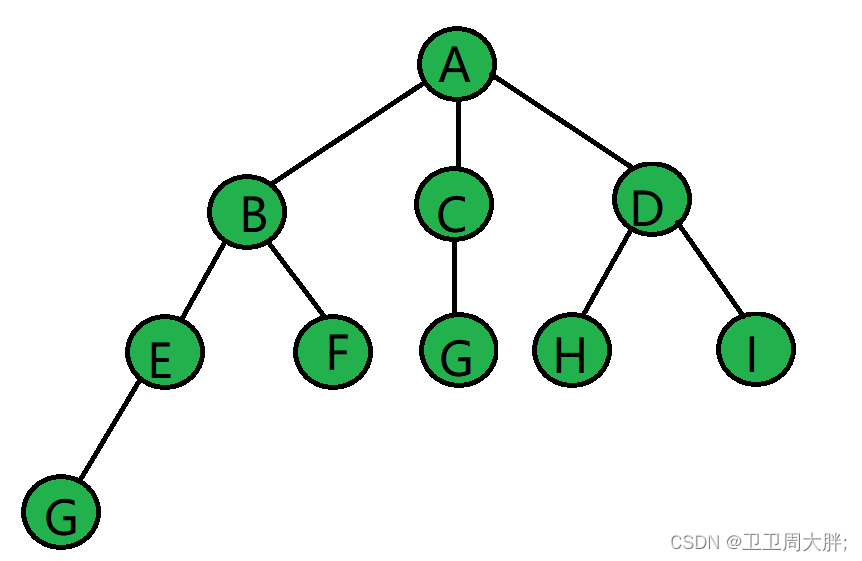
树的相关概念
- 节点的度:一个节点含有的子树的个数称为该节点的度。 如上图:A的为3。
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:F、G、H、I…等节点为叶节点。
- 非终端节点或分支节点:度不为0的节点; 如上图:B、C、D…等节点为分支节点.
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。 如上图:A是B的父节点。
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点。 如上图:B是A的孩子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。 如上图:B、C是兄弟节点。
- 树的度:一棵树中,最大的节点的度称为树的度。 如上图:树的度为5。
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
- 树的高度或深度:树中节点的最大层次。如上图:树的高度为4。
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟。如上图:G、G互为兄弟节点 。
- 节点的祖先:从根到该节点所经分支上的所有节点。如上图:A是所有节点的祖先。
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙。
- 森林:由m(m>0)棵互不相交的树的集合称为森林。
什么是二叉树
二叉树是一种常见的树型数据结构,由若干个节点组成,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树有以下特点(如图所示):
- 每个节点最多有两个子节点,且子节点的位置是固定的。
- 左子节点在父节点的左边,右子节点在父节点的右边。
- 二叉树的子树也是二叉树。
- 二叉树的每个节点都有一个值,可以是任意类型的数据。
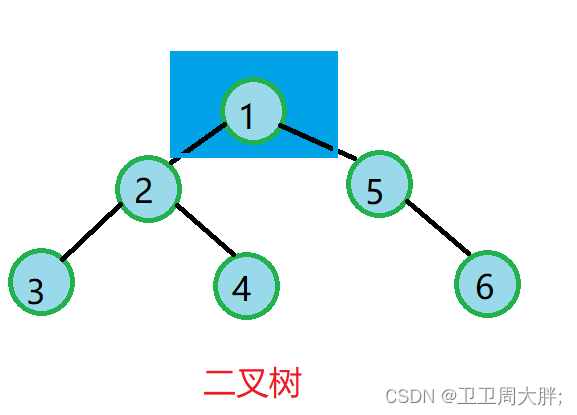
讲完了二叉树的基本性质,我们开始模拟实现二叉树吧!
二叉树的基本功能
- 前序遍历–根、左、右 – 深度优先遍历
- 计算树节点。
- 中序遍历–左、根、右
- 计算叶子节点
- 树的高度
- 求第k层结点的个数
- 二叉树查找值为x的结点
- 通过前序遍历的数组构建二叉树。
- 销毁二叉树
- 层序遍历 – 广度优先遍历
- 判断二叉树是否是完全二叉树
二叉树的初始化(手搓二叉树)
思路导读:由于通过数组创建二叉树比较难,我们先放在博客的后面在去讲解,但是我们又需要二叉树怎么办,那就手搓一个。
代码演示:
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;}TreeNode;TreeNode* BuyNode(int x)
{TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}TreeNode* CreateTree()//创建二叉树
{TreeNode* node1 = BuyNode(1);TreeNode* node2 = BuyNode(30);TreeNode* node3 = BuyNode(2);TreeNode* node4 = BuyNode(71);TreeNode* node5 = BuyNode(99);TreeNode* node6 = BuyNode(11);TreeNode* node7 = BuyNode(21);node1->left = node2;node1->right = node3;node2->left = node4;node2->right = node5;node3->right = node7;node3->left = node6;return node1;
}创建好后的树的结构如下图所示
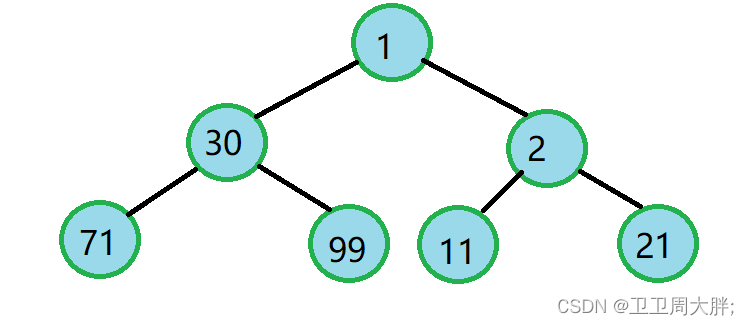
二叉树的前序遍历
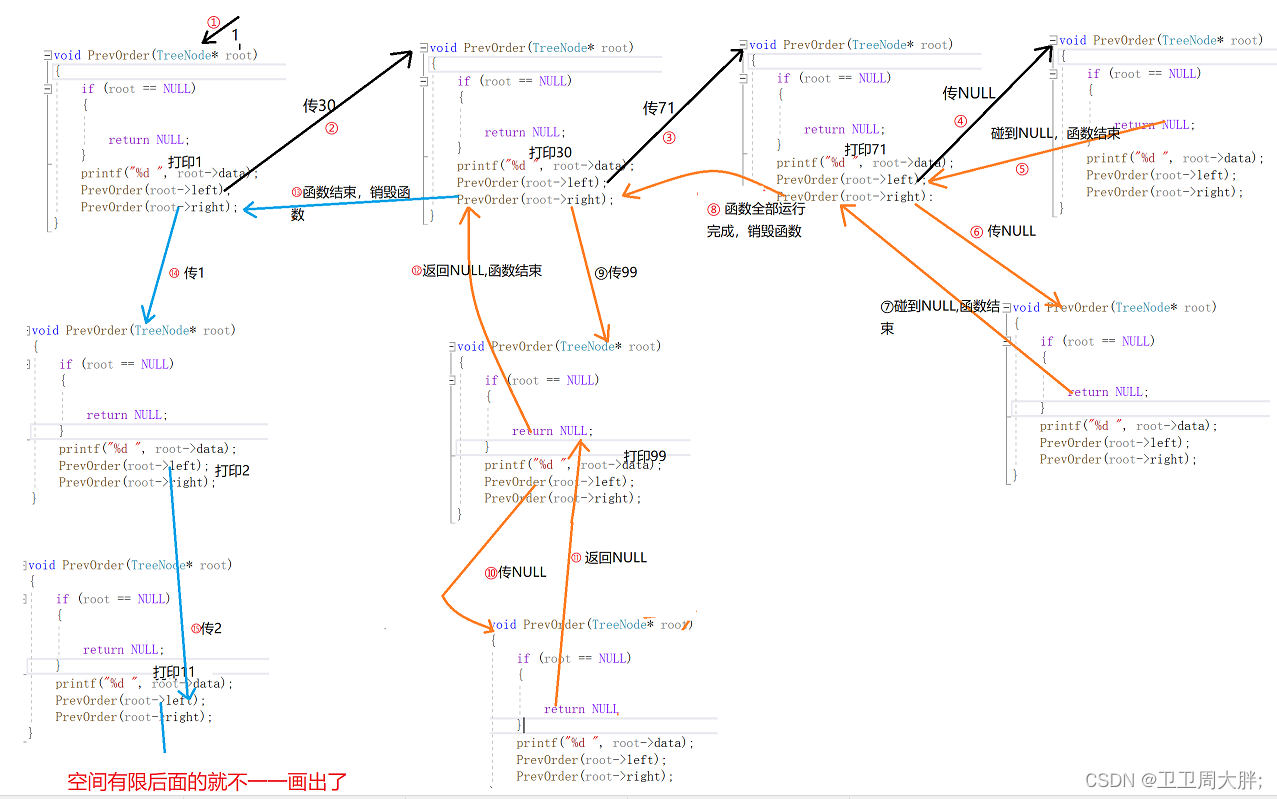
思路导读:二叉树的前序遍历指先遍历二叉树的根,左子树,在遍历右子树。我们可以先画个图来模拟一下它遍历的顺序如下图:
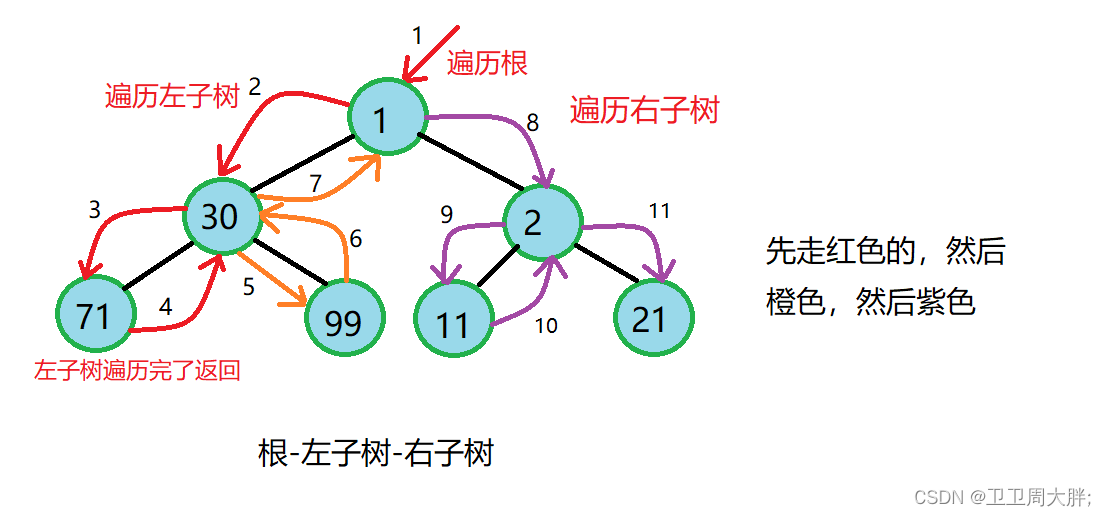
既然图都画出来了,我们肯定思路都大致清晰了,那用什么方式去遍历呢?循环还是什么?今天我们要讲的方式是递归解决二叉树的遍历,这种是目前比较简单的方式。
代码实现:对于刚刚接触二叉树的友友们可能还不能理解这个递归的方式,没事可以看下图的递归展开图帮助你进一步理解
void PrevOrder(TreeNode* root)//前序遍历--根、左、右 -- 深度优先遍历
{if (root == NULL){return NULL;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
运行结果:
二叉树的中序遍历
思路导读:二叉树的中序遍历指先遍历左子树,再遍历根,最后遍历右子树。这个就不为大家再画递归展开图了,看代码!
代码演示:
void InOrder(TreeNode* root)//中序遍历--左、根、右
{if (root == NULL){return NULL;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}运行结果:
计算树节点
思路导读:我们要想计算树节点的个数,我们只需要将其左子树,右子树,还有根的值全部算出有多少即可,我们只需通过像前序遍历的思想来计算。如果不懂的话可以看下面的递归展开图(博主就画了前几步)。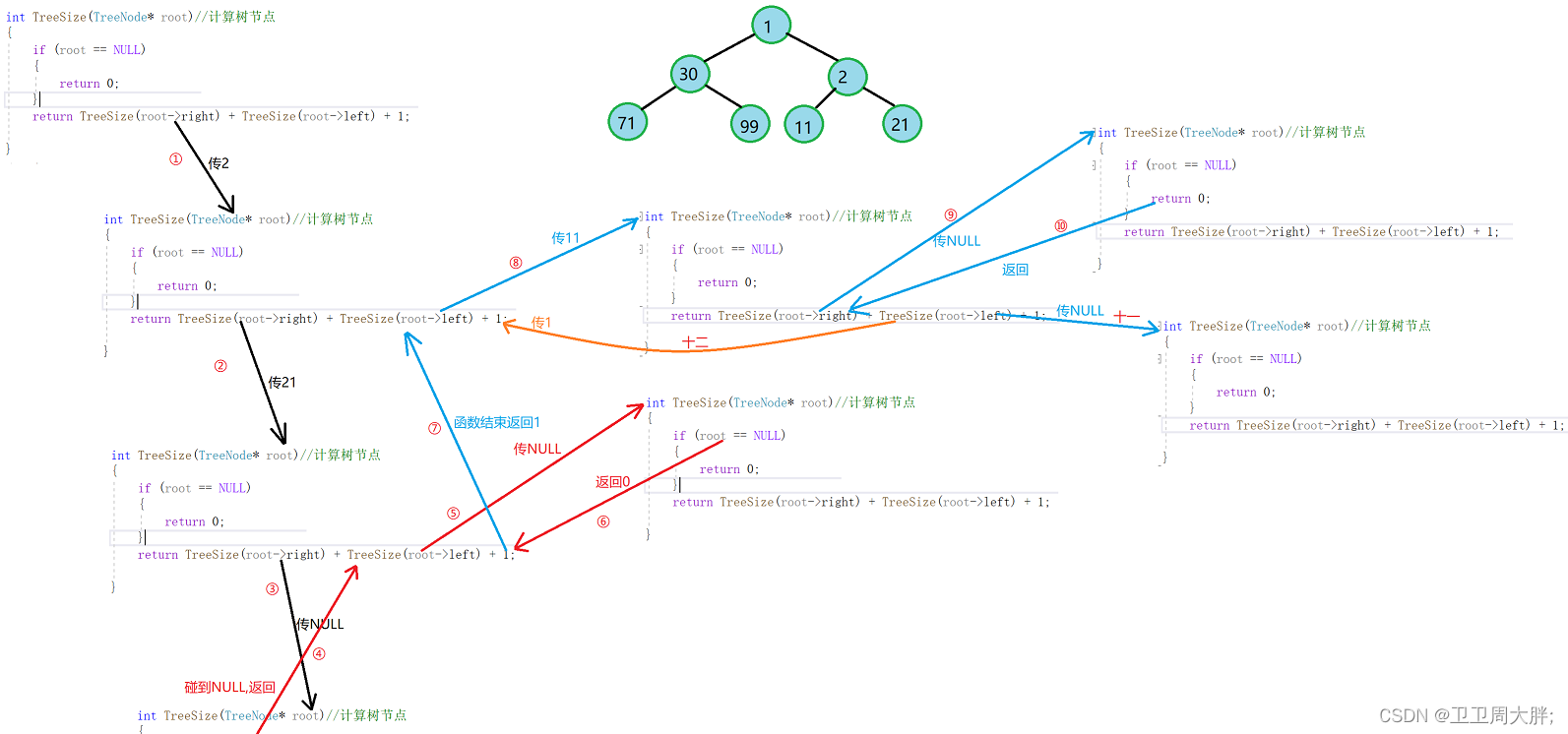
代码实现:
int TreeSize(TreeNode* root)//计算树节点
{if (root == NULL){return 0;}return TreeSize(root->right) + TreeSize(root->left) + 1;}
计算叶子节点
思路导读:我们可以通过遍历该树的左子树和右子树,如果左子树和右子树同时为NULL我们就让它返回1,以此类推,我们可以通过像前面一样的方式遍历二叉树达到计算叶子节点的效果(部分递归展开图)。
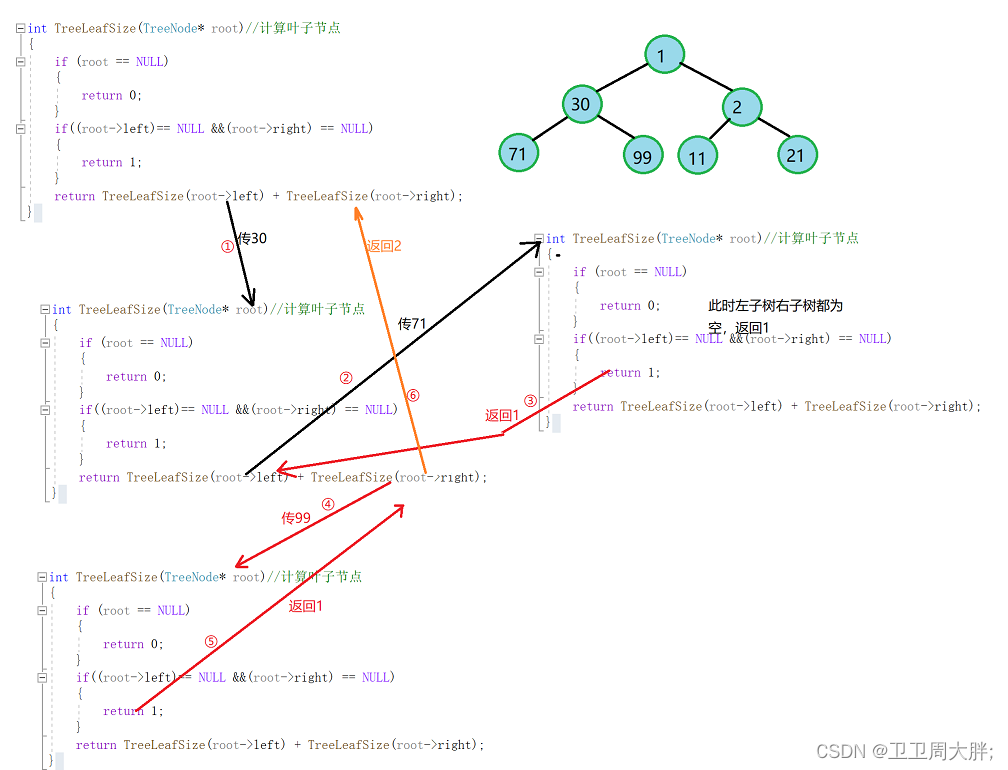
代码实现:
int TreeLeafSize(TreeNode* root)//计算叶子节点
{if (root == NULL){return 0;}if((root->left)== NULL &&(root->right) == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}计算树的高度
思路导读:计算树的高度我们可以通过比较它的左子树和右子树找出其树高度中较大的那个然后加上一即可算出来这个树的高度,怎么比较呢?那我们就可以通过利用fmax这个函数来比较其找到最大值。
(部分递归展开图如下)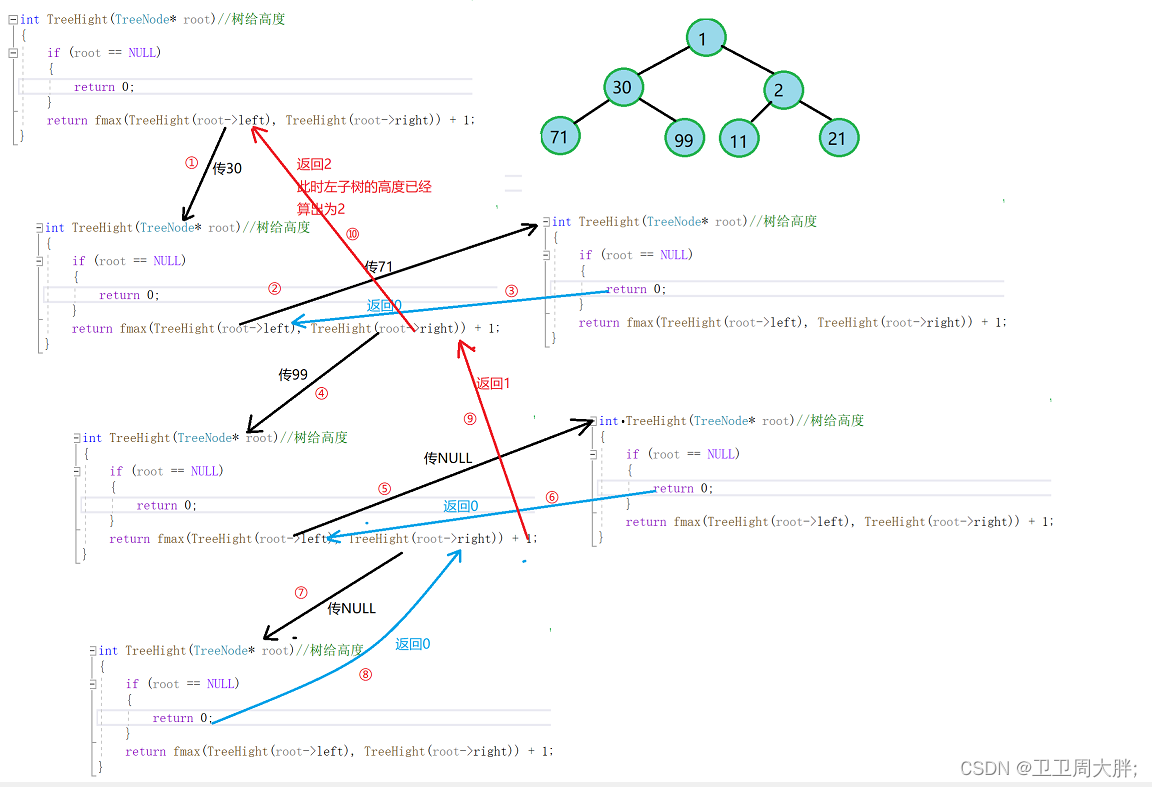
代码实现:
int TreeHight(TreeNode* root)//树给高度
{if (root == NULL){return 0;}//fmax函数,它是C语言(C99)中的一个内置函数,用于比较两个浮点数的大小并返回较大值。return fmax(TreeHight(root->left), TreeHight(root->right)) + 1;
}
求第k层节点的个数
思路导读:要想求第k层节点的个数我们需要将该层中左子树和右子树的位置分别记录下来,然后将其相加就是该层的个数。那么另一个问题来了,我们如何找到是这一层呢?我们可以通过每让它往下走一层时,就让k-1,依次递归,当k完全等于1的时候说明已经到了这一层,再返回1即可。(递归展开图如下)
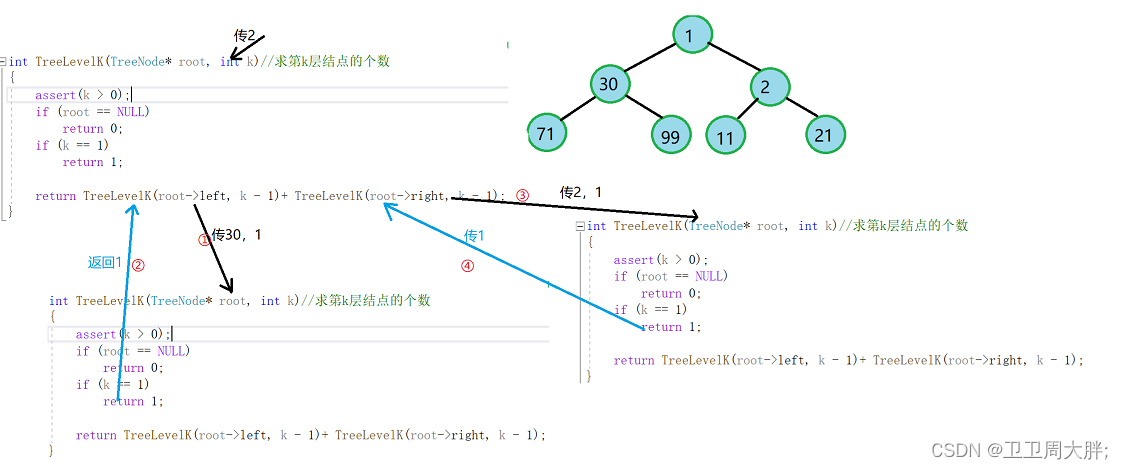
代码实现:
int TreeLevelK(TreeNode* root, int k)//求第k层结点的个数
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;二叉树查找值为x的节点
思路导读:我们通过前面写了这么多的二叉树的接口,这里我们可以想到,我们先查左子树中是否有相同的,然后我们再去查看右子树中是否有相同的,如果左子树找到了就将该值返回即可。(部分递归展开图如下)
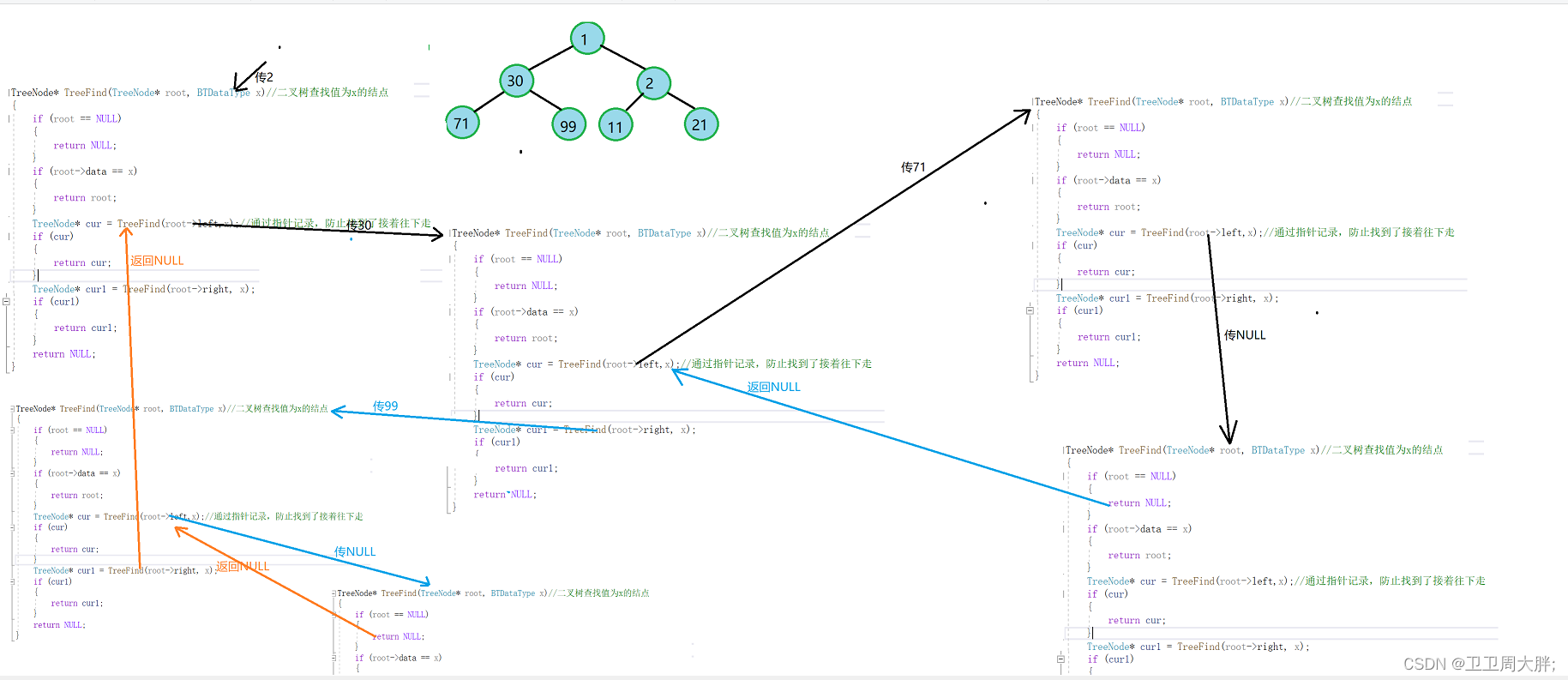
代码实现:
TreeNode* TreeFind(TreeNode* root, BTDataType x)//二叉树查找值为x的结点
{if (root == NULL){return NULL;}if (root->data == x){return root;} TreeNode* cur = TreeFind(root->left,x);//先找左子树,通过指针记录,防止找到了接着往下走if (cur){return cur;}TreeNode* cur1 = TreeFind(root->right, x);//再找右子树,同理指针记录if (cur1){return cur1;}return NULL;
}
通过前序遍历的数组构建二叉树
我们先假定传来的数组为:char arr[] = { 'A','B','D','#','#','E','#','H','#','#','C','F','#','#','G','#','#' };
该’#'代表NULL,因此我们先画出其前序遍历的展开图(如下):

然后我们只需要像前序遍历一样,将其按照根、左子树、右子树一样依次开辟结点赋值,此时我们要注意的是一定要使用指针,防止在递归的过程中其值不会变化。
代码实现如下:
TreeNode* TreeCreate2(char* a, int* pi)//通过前序遍历的数组构建二叉树
{if (*(a + *pi) =='#'){(*pi)++;return NULL ;}TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));root->data = *(a + (*pi)++);root->left = TreeCreate2(a, pi);root->right = TreeCreate2(a, pi);return root;
}
运行结果:

二叉树的销毁
思路导读:二叉树的销毁可以像二叉树的后序遍历一样先左子树、右子树
代码实现:
void DestoryTree(TreeNode* root)//销毁
{if (root == NULL){return NULL;}DestoryTree(root->left);DestoryTree(root->right);free(root);}
层序遍历 – 广度优先遍历
思路导读:我们知道二叉树的一个特性,每一个节点都有俩个子节点,因此我们在可以充分的利用这个特性来实现我们层序遍历,我们可以模拟实现一个队列,让二叉树的根先存进去队列,然后打印其数据,就打印了第一层的数据,此时我们要打印第二层的数据,我们只需要将根的左子树和右子树在分别存入队列,在第二次循环中在依次打印即可实现层序遍历了。记住一定在队列中存的是二叉树根的地址而不是值(如下图所示)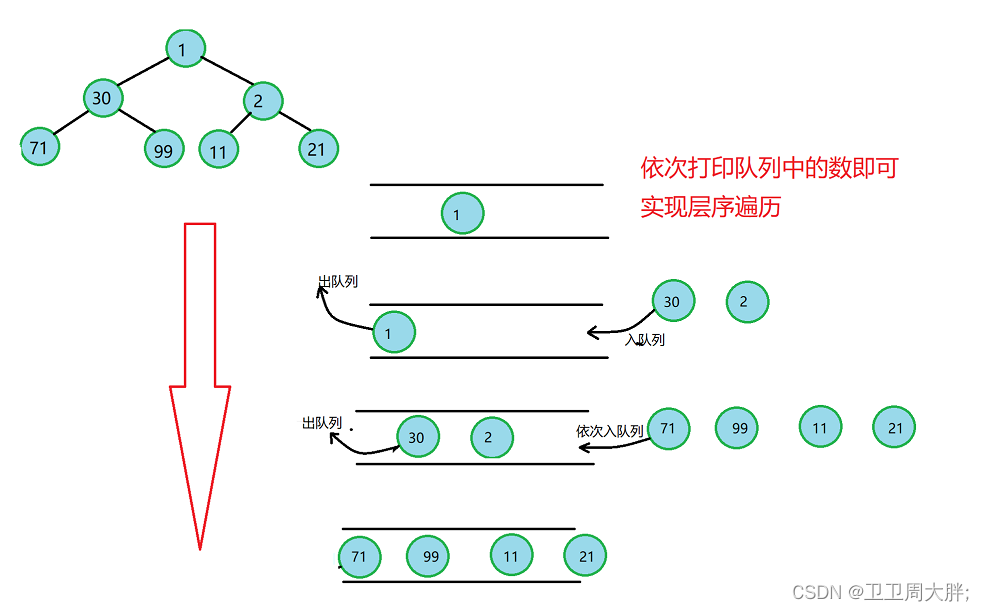
代码实现:
void levelorder(TreeNode* root)//层序遍历 -- 广度优先遍历
{QNode q1;QueueInit(&q1);// TreeHight(root);if (root){//QueuePush(Queue * pq, QDataType x)QueuePush(&q1, root);}int level = 1;while (!QueueEmpty(&q1)){while (level--){TreeNode* front = QueueFront(&q1);//将头元素地址保存在二叉树中QueuePop(&q1);printf("%c ", front->data);if (front->left){QueuePush(&q1, front->left);}if (front->right){QueuePush(&q1, front->right);}}level = QueueSize(&q1);printf("\n");}QueueDestroy(&q1);
测试函数:
void Test1()
{TreeNode* root = CreateTree1();char arr[] = { 'A','B','D','#','#','E','#','H','#','#','C','F','#','#','G','#','#' };int i = 0;levelorder(TreeCreate2(arr, &i));
}
运行结果:
判断是否是完全二叉树
思路导读:我们可以像前面一样,让它们依次层次入队列,如果在入队列的过程中就碰到了NULL,就说明其不是完全二叉树,然后再将最后一层中队列的元素依次出队列,如果出队列的途中也碰到了NULL也就说明其不是完全二叉树。如果都没碰到则是完全二叉树。
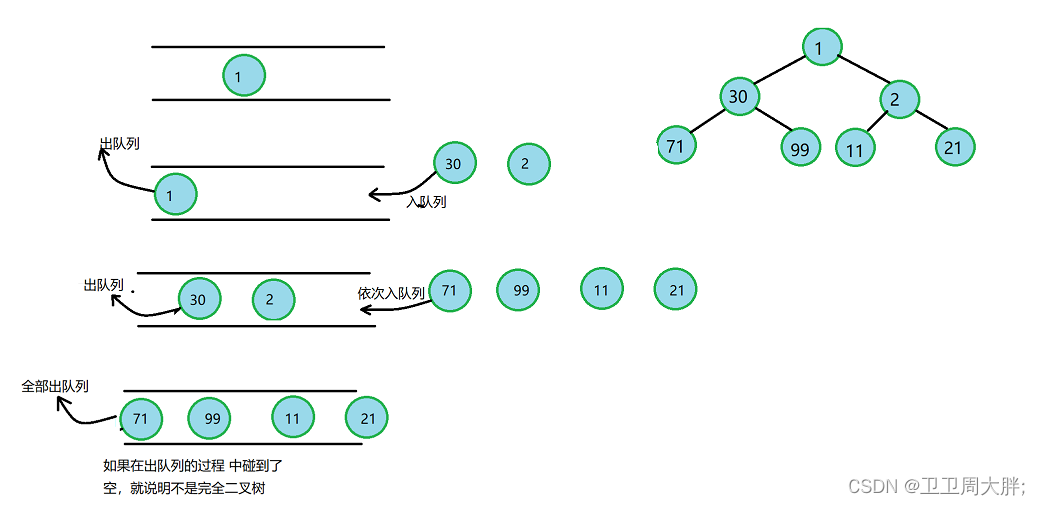
代码实现:
bool TreeComplete(TreeNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);}// 前面遇到空以后,后面还有非空就不是完全二叉树while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
结语:今天的内容就到这里吧,谢谢各位的观看,如果有讲的不好的地方也请各位多多指出,作者每一条评论都会读的,谢谢各位。





)
九-EMI 滤波器容性电流影响分析)






)

正反向转换)
技术支撑单位)



