大模型 RLHF 实战

• • 大模型 RLHF 实战
  • RLHF：OpenAI独家绝技
  • • RLHF 的问题
  • DPO 直接偏好优化算法：RLHF的替代算法
  • • 公式 1 - 4：KL散度下奖励的最大化目标
    • 使用 DPO 微调 Llama 2
  • RAIHF

 

---

大模型 RLHF 实战

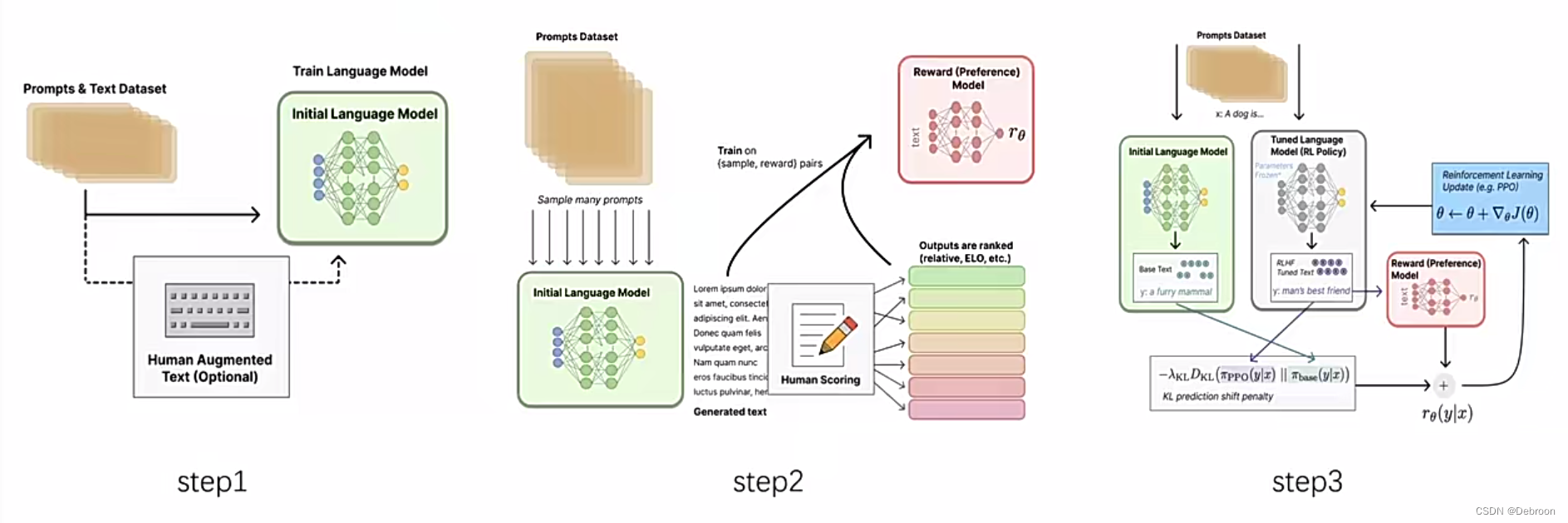
RLHF（基于人类反馈的强化学习）分为 3 个阶段：

• 预训练：为了生成内容，需要一个生成式的预训练语言模型（如GPT）；还会引入微调，帮助模型更好理解提示（Prompts）
• 训练奖励函数：通过对模型生成的结果，人工标注反馈，构造训练集，用于训练奖励函数，模拟人的奖励偏好
• 强化学习：定义策略（第一阶段语言模型输入输出）、动作空间（词表token的排列组合）、奖励函数（第二阶段训练的）；对于同一个问题，会同时送入原始模型、训练模型，用奖励函数对俩者评分，分数差值用于训练策略函数。

安利下面的工具，支持主流模型（ChatGLM系列、Baichuan系列、LLaMA系列、Qwen系列、Bloom）：

• https://github.com/littepan/LLaMA-Efficient-Tuning/blob/main/README_zh.md

• https://github.com/hiyouga/LLaMA-Factory

同时支持训练方法，包括预训练(pre-training), 有监督微调（sft）和 RLHF，微调方式均为 LoRA 或者 QLoRA、全参数。

按照ta的教程一步步操作即可。

RLHF：OpenAI独家绝技

正在更新…

RLHF 的问题

RLHF 的替代有 2 种：DPO、RAIHF。

• RLHF：从人类反馈中学习的强化学习

• DPO：直接偏好优化算法，专门替代传统的基于奖励的 RL 方法。

  RLHF 问题：策略和价值函数迭代步骤相当复杂，经验数据采集计算成本高。

  改进：DPO 是简化了 RLHF 步骤（不需要对奖励函数进行复杂的工程设计），但同时效果不比 RLHF 差。

• RAIHF：RLHF不再需要人类，AI 实现标注自循环，AI标注效果一样好。

  RLHF 问题：

  • 成本高昂（收集高质量人工，反馈需要大量的时间和金钱资源），RLHF通常使用数以万计的人类偏好标签
  • 样本效率低（模型需要大量的人类反馈来学习和改进其行为）
  • 人类偏见（模型可能会学习并放大人类评估者的偏见）
  • 一致性问题（不同人评估给出不一致的反馈，导致模型训练中的不确定性）
  • 可扩展性问题（对于非常复杂的任务或环境，难以获得足够的人类反馈来训练模型）
     

  改进：RAIHF 是通过 AI 排序，而非人工排序数据集，训练出来的偏好模型PM的指引下迭代模型策略。

DPO 直接偏好优化算法：RLHF的替代算法

论文地址：https://arxiv.org/abs/2305.18290

作者在训练 DPO 模型时省略了奖励模型训练的步骤，而是通过设计一种包含正负样本对比的损失函数，在训练过程中得到一个满足人类偏好的模型。

• 你的语言模型其实是一个奖励模型
• 不训练奖励模型，语言模型直接做偏好优化
• 学习你的偏好，满足你的偏好

这种方法在文本总结和单轮对话任务上提高了生成结果的质量。

正样本和负样本的对比，使得模型能够更好地学习到人类偏好的特征，从而提升了生成的质量。

RLHF、DPO 差异：

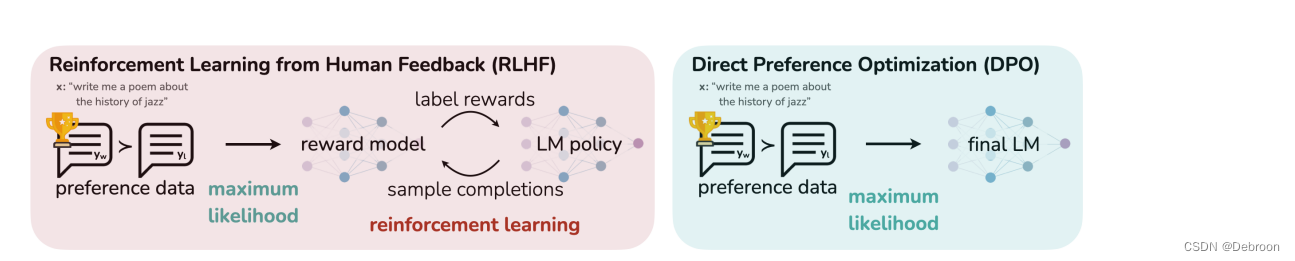
左右两边最大的区别就是，有没有reward model (RM)。

DPO 是将配给 RW 的训练融合在 final LM 里面，LLM本身即是RM。

公式 1 - 4：KL散度下奖励的最大化目标

$p^{\ast }(y_1\succ y_2\mid x)=\frac{\exp \left(r^{\ast }(x,y_1)\right)}{\exp \left(r^{\ast }(x,y_1)\right)+\exp \left(r^{\ast }(x,y_2)\right)}$

• 人类偏好分布 $p\ast$
• 模型会生成问答对，会呈现给人类标注者，并让他们给出一个答案偏好 $y_1>y_2|x$
• $y_1>y_2$：更好的答案
• 假设这些偏好是由某个潜在的奖励模型 $r^{\ast }(x,y_1)$ 生成

建立奖励模型，对其参数做最大似然估计，从而将问题转换为二分类问题，同时使用负对数做似然损失：

• ${\mathcal{L}}_R(r_{\varphi },\mathcal{D})=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}[\log \sigma (r_{\varphi }(x,y_w)-r_{\varphi }(x,y_l))]$

目标函数（使用学到的奖励函数来为语言模型提供反馈）：

• ${\max }_{{\pi }_{\theta }}{\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(y|x)}[r_{\varphi }(x,y)]-\beta {\mathbb{D}}_{\mathbf{KL}}[{\pi }_{\theta }(y\mid x)||{\pi }_{\mathbf{ref}}(y\mid x)]$

推导上式，得到：

• ${\pi }_r(y\mid x)=\frac{1}{Z(x)}{\pi }_{\mathrm{ref}}(y\mid x)\exp \left(\frac{1}{\beta }r(x,y)\right)$
   

上述就是论文 1 - 4 的推导结果。

这个公式是从一个最大化目标函数出发来推导的，其中包含了两个部分：模型预期奖励的最大化以及KL散度的一个约束项。

KL散度是衡量两个概率分布之间差异的一个指标，在这里用于限制学习到的策略 ${\pi }_{\theta }$ 与参考策略 ${\pi }_{\mathrm{ref}}$ 之间的差异。

目标函数可以分解为两部分：

1. ${\max }_{{\pi }_{\theta }}{\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(y|x)}[r_{\varphi }(x,y)]$

   • 这部分表示模型试图最大化预期奖励，也就是在给定输入 $x$ 的情况下，通过策略 ${\pi }_{\theta }$ 生成答案 $y$ 来获得尽可能高的奖励 $r_{\varphi }(x,y)$。

2. $-\beta {\mathbb{D}}_{\mathbf{KL}}[{\pi }_{\theta }(y\mid x)||{\pi }_{\mathbf{ref}}(y\mid x)]$

   • 这部分表示有一个正则化项，通过KL散度来限制策略 ${\pi }_{\theta }$ 不能偏离参考策略 ${\pi }_{\mathrm{ref}}$ 太远。$\beta$ 是一个正的权衡系数，决定了对偏离的惩罚程度。

目标函数最大，而公式 3 是相减，就意味着 $-\beta {\mathbb{D}}_{\mathbf{KL}}[{\pi }_{\theta }(y\mid x)||{\pi }_{\mathbf{ref}}(y\mid x)]$ 要最小。

而要从这个目标函数推导出策略 ${\pi }_r(y\mid x)$ 的表达式，我们需要用到拉格朗日乘子法来处理带有约束的优化问题。拉格朗日乘子法可以帮助我们求解在某些约束条件下的最优化问题。

在这种情况下，想要的是一个新的策略 ${\pi }_r(y\mid x)$，不仅能最大化奖励，还要满足对参考策略 ${\pi }_{\mathrm{ref}}(y\mid x)$ 的约束。

为了解这个带约束的优化问题，可以构建一个拉格朗日函数：

$$\mathcal{L}({\pi }_{\theta })={\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(y|x)}[r_{\varphi }(x,y)]-\beta {\mathbb{D}}_{\mathbf{KL}}[{\pi }_{\theta }(y\mid x)||{\pi }_{\mathbf{ref}}(y\mid x)]$$

对这个函数求解最优策略 ${\pi }_{\theta }$ 的表达式时，会发现最优策略具有如下形式：

• 公式 3 到 公式 4 的详细推导：https://zhuanlan.zhihu.com/p/644911957

$${\pi }_r(y\mid x)=\frac{1}{Z(x)}{\pi }_{\mathrm{ref}}(y\mid x)\exp \left(\frac{1}{\beta }{r}_{\varphi }(x,y)\right)$$

这里的 $Z(x)$ 是规范化因子（相当于做了归一化，取值 0-1），确保 ${\pi }_r(y\mid x)$ 是一个有效的概率分布。

这个推导使用了变分原理，其中 ${\pi }_r(y\mid x)$ 是 ${\pi }_{\theta }(y\mid x)$ 的一个特殊形式，它使得拉格朗日函数 $\mathcal{L}({\pi }_{\theta })$ 被最大化。

意思是，可以通过一个加权的参考策略来构造一个新的策略，该策略会偏向于高奖励的行为，同时保持与参考策略的相似性。

权重由奖励函数和温度参数 $\beta$ 共同决定。

正在更新…

使用 DPO 微调 Llama 2

请猛击：https://github.com/huggingface/blog/blob/main/zh/dpo-trl.md

RAIHF