【数据结构】八大排序之简单选择排序算法

🦄个人主页:修修修也

🎏所属专栏:数据结构

⚙️操作环境:Visual Studio 2022

一.简单选择排序简介及思路

二.简单选择排序的代码实现

三.简单选择排序的优化

四.简单选择排序的时间复杂度分析

结语

一.简单选择排序简介及思路

简单选择排序算法(Simple Selection Sort)是一种简单直观的选择排序算法.

它的基本操作是:

每一次通过n-i次关键字间的比较,从n-i+1个数据中选出关键字最小(大)的数据,并和第i(1≤i≤n)个数据交换
重复n-1次上述操作,直到全部待排序的数据元素排完.

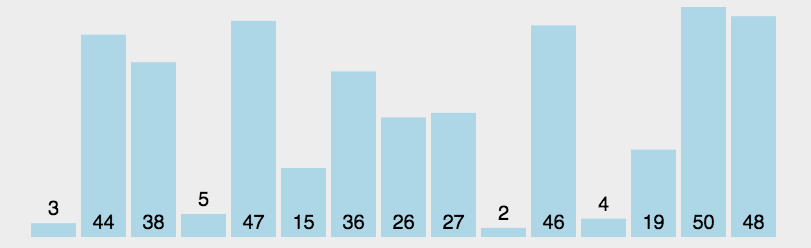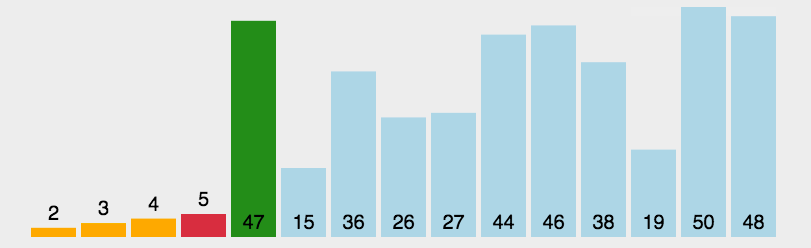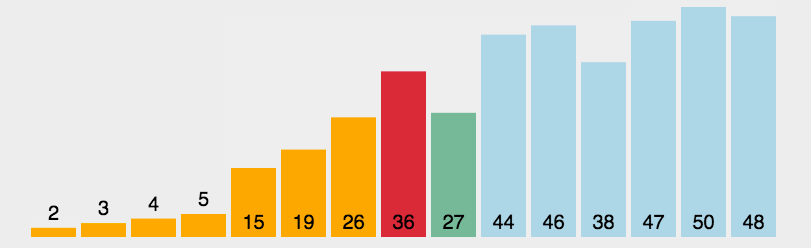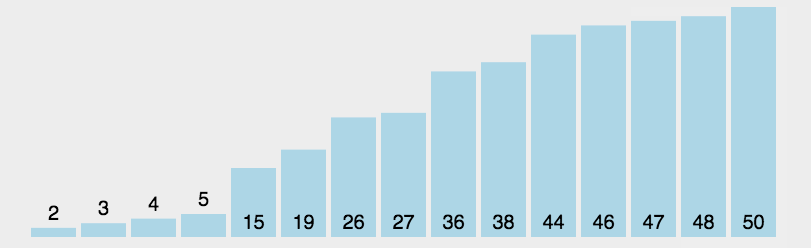
算法动图演示如下:

二.简单选择排序的代码实现

算法实现步骤:(以升序为例)

在元素集合arr[i]~arr[n-1]中选择关键码最小(大)的数据元素.
若它不是这组元素中的第一个(最后一个)元素,则将它与这组元素中的第一个(最后一个)元素交换.
在剩余的arr[i+1]~arr[n-1](arr[i]~arr[n-2])集合中,重复上述步骤,直到集合剩余一个元素.

清楚了实现步骤后,代码的实现就比较简单了,代码如下:

//交换函数
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//直接选则排序(升序
void SelectSort(int* a, int n)
{int left = 0;while (left < n - 1){int mini = left;for (int i = left + 1; i <= n - 1; i++){if (a[i] < a[mini]){mini = i;}}Swap(&a[left], &a[mini]);left++;}
}

三.简单选择排序的优化

我们在设计简单选择排序时,思路往往都是每趟循环选出一个最大或最小的将其放在相应位置上,那么其实我们可不可以一趟直接将最大和最小的两个元素都选出来呢?

依照这个思路,我们对简单选择排序进行优化,使其一趟就可以将最大的元素和最小的元素都选出来交换到相应的位置上,综上,代码实现如下:

//交换
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//选择排序(直接选择排序)
void SelectSort(int* a, int n)
{//优化:一趟选出最大和最小的int left = 0;int right = n - 1;while (left < right){int mini = left, maxi = left;for (int i = left + 1; i <= right; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[left], &a[mini]);//如果left和maxi重叠,交换后需要修正一下再交换right和maxiif (left == maxi){maxi = mini;}Swap(&a[right], &a[maxi]);left++;right--;}
}

注意:

当我们在一趟比较结束后选出mini和maxi并做交换的时候,要小心如果left记录的位置恰好存放的是maxi,则第一步交换left和mini后我们就要重新对maxi的位置做一个修正,如图:

四.简单选择排序的时间复杂度分析

我们可以发现,简单选择排序的特点是:

         元素挪动交换次数很少,但是元素比较次数很多,并且无论是数组天生顺序的情况还是天生逆序的情况,元素比较次数都是一样的,都是:T(n)=(n-1)+(n-2)+...+2+1=n(n-1) / 2 次.

          而对于交换次数而言,最好的时候,交换次数为0次,最坏的时候,交换次数为n-1次.

          基于最终的排序时间是交换次数和比较次数的总和,因此,总的时间复杂度依然是O(n^2).

结语

希望这篇简单选择排序算法详解能对大家有所帮助,欢迎大佬们留言或私信与我交流.

有关更多排序相关知识可以移步:

【数据结构】八大排序算法https://blog.csdn.net/weixin_72357342/article/details/135038495?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135038495%22%2C%22source%22%3A%22weixin_72357342%22%7D&fromshare=blogdetail