数字滤波器设计——Matlab实现数字信号处理＜1＞

目录

一.实验内容

二.代码分析

1.信号产生部分

2.利用傅立叶级数展开的方法，自由生成所需的x(t)

3.通过选择不同的采样间隔T（分别选T>或<1/2fc），从x(t)获得相应的x(n)

3.对获得的不同x(n)分别作傅立叶变换，分析其频率响应特性（给出幅频与相频特性曲线）

4.利用巴特沃思滤波器设计数字滤波器

<1>低通滤波器

<2>高通滤波器

<3>绘图

5.利用窗函数设计法或频率采样法设计数字滤波器

<1>高通滤波器

<2>低通滤波器

<3>绘图

三.实验结果

一.实验内容

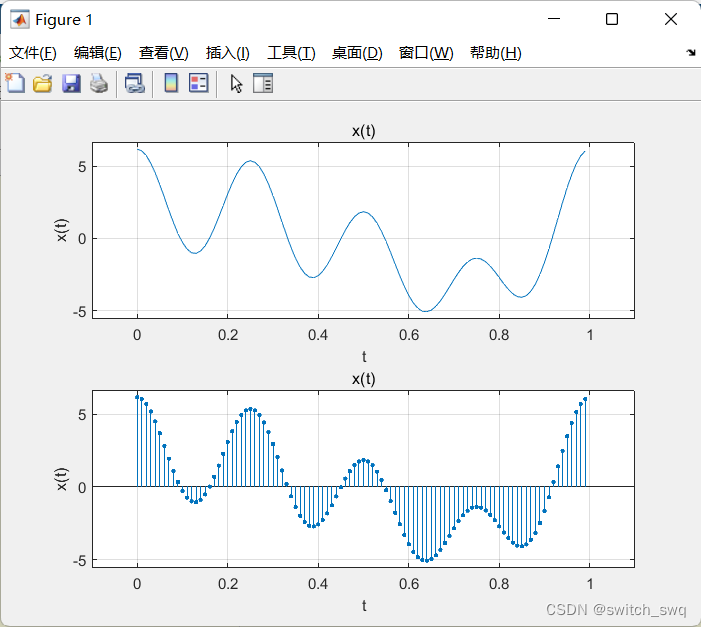
1．利用傅立叶级数展开的方法，自由生成所需的x(t)；

2．通过选择不同的采样间隔T（分别选T>或<1/2fc），从x(t)获得相应的x(n)（作出x(n)图形）；

3．对获得的不同x(n)分别作傅立叶变换，分析其频率响应特性（给出幅频与相频特性曲线）；

4．利用巴特沃思、切比雪夫或椭圆滤波器设计数字滤波器（滤波特性自定），要求通过改变滤波器参数或特性（低通、高通、带通或带阻）设计至少两种数字滤波器，分析所设计滤波器（画出频率特性曲线），并对上述给出的不同x(n)分别进行滤波（画出滤波结果），然后加以讨论；

5．利用窗函数设计法或频率采样法设计数字滤波器（滤波特性自定），要求通过改变滤波器参数或特性（低通、高通、带通或带阻等）设计至少两种数字滤波器，分析所设计滤波器（画出频率特性曲线），并对上述给出的不同x(n)分别进行滤波（画出滤波结果），然后加以讨论。

二.代码分析

1.信号产生部分
function [signal]=signal_xt(t_length,T,f,A,u)
%%  函数描述
%   功能：利用傅立叶级数展开的方法，自由生成所需的x(t)（不含直流量）；
%   输入参数：产生序列的长度t_length；采样间隔T；f(t)的基波频率f；傅立叶级数展开的各项幅值和相位。故最高频率为fc=length(A)*f
%   使用举例：signal=signal_xt(3,0.01,1,[1,2,3,4],[0,1,0,1])
%%  t,y初始化并计算
t=0:T:t_length-T;
t_num=t_length/T;
signal=zeros(1,t_num);
max=0;
min=0;
for i=1:t_num  for k=1:length(A)%   计算函数值signal(i)= signal(i) + A(k)*cos(2*pi*k*t(i)*f+u(k));%   最大最小值记录if max<signal(i)max=signal(i);endif min>signal(i)min=signal(i);endend
end
%%  结果展示
figure;
subplot(2,1,1);
plot(t,signal);
%   x，y轴范围限制及标题
axis([0-0.1,t_length+0.1,min-0.5,max+0.5])
title('x(t)'); 
xlabel('t');
ylabel('x(t)'); 
grid onsubplot(2,1,2);
stem(t,signal,".");
%   x，y轴范围限制及标题
axis([0-0.1,t_length+0.1,min-0.5,max+0.5])
title('x(t)'); 
xlabel('t');
ylabel('x(t)'); 
grid on

function [signal]=signal_xt(t_length,T,f,A,u)
%%  函数描述
%   功能：利用傅立叶级数展开的方法，自由生成所需的x(t)（不含直流量）；
%   输入参数：产生序列的长度t_length；采样间隔T；f(t)的基波频率f；傅立叶级数展开的各项幅值和相位。故最高频率为fc=length(A)*f
%   使用举例：signal=signal_xt(3,0.01,1,[1,2,3,4],[0,1,0,1])

2.利用傅立叶级数展开的方法，自由生成所需的x(t)
%%  利用傅立叶级数展开的方法，自由生成所需的x(t)，即signal_origin；
t_length=1;     %生成长度
f=1;            %基础频率
A=[3,1,1,3];    %各项幅度
u=[-1,0,1,0];   %各项相位
signal_origin=signal_xt(t_length,0.01,f,A,u);
fc=f*length(A);
3.通过选择不同的采样间隔T（分别选T>或<1/2fc），从x(t)获得相应的x(n)
%%  通过选择不同的采样间隔T（分别选T>或<1/2fc），从x(t)获得相应的x(n)；
T=[1/(2*fc+1),1/fc,1/(4*fc)];
N=zeros(1,length(T));
for i=1:length(T)N(i)=1/T(i);
end
x1=signal_xt(t_length,T(1),f,A,u);
x2=signal_xt(t_length,T(2),f,A,u);
x3=signal_xt(t_length,T(3),f,A,u);

选取频率分别为2fc+1、fc、4fc

3.对获得的不同x(n)分别作傅立叶变换，分析其频率响应特性（给出幅频与相频特性曲线）
%%  对获得的不同x(n)分别作傅立叶变换，分析其频率响应特性（给出幅频与相频特性曲线）；
X1=fft(x1,N(1));
X2=fft(x2,N(2));
X3=fft(x3,N(3));%   绘制
figure;
%   幅值绘制
subplot(2,3,1);
stem(0:N(1)-1,abs(X1),'.');
title("X1");
grid onsubplot(2,3,2);
stem(0:N(2)-1,abs(X2),'.');
title("X2");
grid onsubplot(2,3,3);
stem(0:N(3)-1,abs(X3),'.');
title("X3");
grid on%   相位绘制
subplot(2,3,4);
stem(0:N(1)-1,angle(X1),'.');
title("X1");
grid onsubplot(2,3,5);
stem(0:N(2)-1,angle(X2),'.');
title("X2");
grid onsubplot(2,3,6);
stem(0:N(3)-1,angle(X3),'.');
title("X3");
grid on

使用 fft 函数进行 DFT，注意结果频率响应是复数，使用abs函数得其幅值，angle函数得其相位。

4.利用巴特沃思滤波器设计数字滤波器
<1>低通滤波器
%   设置低通滤波器参数
wp=0.35;    %通带边界频率
ws=0.7;     %阻带截止频率
Rp=3;
As=15;
%   计算滤波器阶数N和3dB截止频率wc
[Nc,wc]=buttord(wp,ws,Rp,As,'s');
%   计算滤波器系统函数分子分母多项式系数
[Bz,Az]=butter(Nc,wc,'low');
wk=64;
Hk=freqz(Bz,Az,wk);

参数设置及函数使用参考课本《数字信号处理》

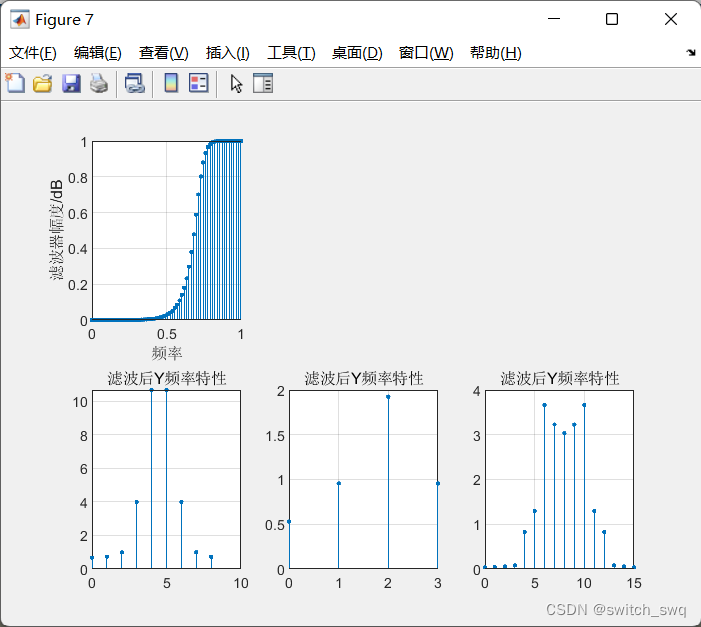
<2>高通滤波器
%   设置高通滤波器参数
wp=0.75;
ws=0.5;
rp=3;
rs=15;
[Nc,wc]=buttord(wp,ws,rp,rs,'s');
[Bz,Az]=butter(Nc,wc,'high');
wk=64; 
Hk=freqz(Bz,Az,wk);
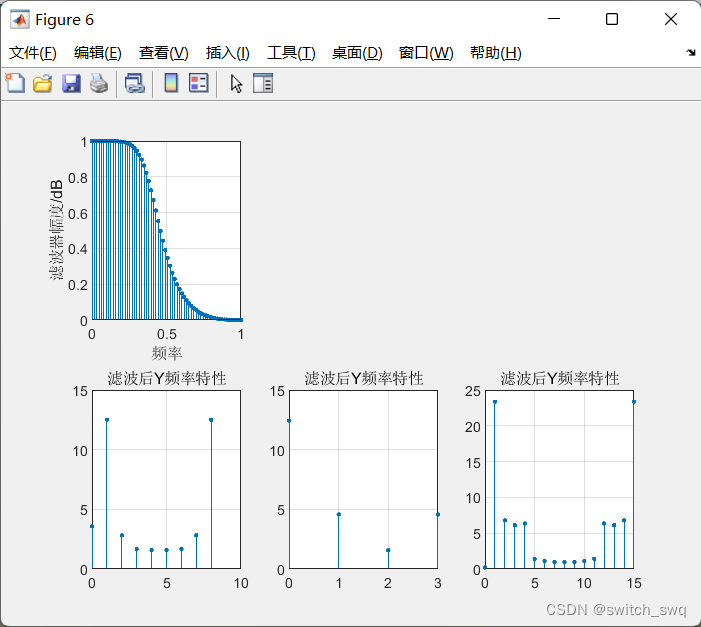
<3>绘图
%   绘图
figure;
subplot(2,3,1);
stem(0:1/63:1,abs(Hk),'.');
xlabel('频率');
ylabel('滤波器幅度/dB');
grid on%   滤波后结果
m1=filter(Bz,Az,x1);
m2=filter(Bz,Az,x2);
m3=filter(Bz,Az,x3);
Y1=fft(m1,N(1));
Y2=fft(m2,N(2));
Y3=fft(m3,N(3));
%   绘图
subplot(2,3,4);
stem(0:N(1)-1,abs(Y1),'.');
title('滤波后Y频率特性');
grid on
subplot(2,3,5);
stem(0:N(2)-1,abs(Y2),'.');
title('滤波后Y频率特性');
grid on
subplot(2,3,6);
stem(0:N(3)-1,abs(Y3),'.');
title('滤波后Y频率特性');
grid on
5.利用窗函数设计法或频率采样法设计数字滤波器
<1>高通滤波器
%   设置高通滤波器参数
wp=pi/2;
ws=pi/4;
Bt=wp-ws;   %过渡带宽度
N0=ceil(6.2*pi/Bt); %汉宁窗计算所需h(n)长度N0
Nn=N0+mod(N0+1,2);  %确保h(n)长度为奇数
wc=(wp+ws)/2/pi;    %理想高通滤波器通带截止频率
hn=fir1(Nn-1,wc,'HIGH',hanning(Nn));
%   高通滤波器频率响应
Hk=fft(hn,length(hn));
<2>低通滤波器
%   设置低通滤波器参数
wp=pi/4;
ws=pi/2;
Bt=abs(wp-ws);   %过渡带宽度
N0=ceil(6.2*pi/Bt); %汉宁窗计算所需h(n)长度N0
Nn=N0+mod(N0+1,2);  %确保h(n)长度为奇数
wc=(wp+ws)/2/pi;    %理想高通滤波器通带截止频率
hn=fir1(Nn-1,wc,'LOW',hanning(Nn));
%   低通滤波器频率响应
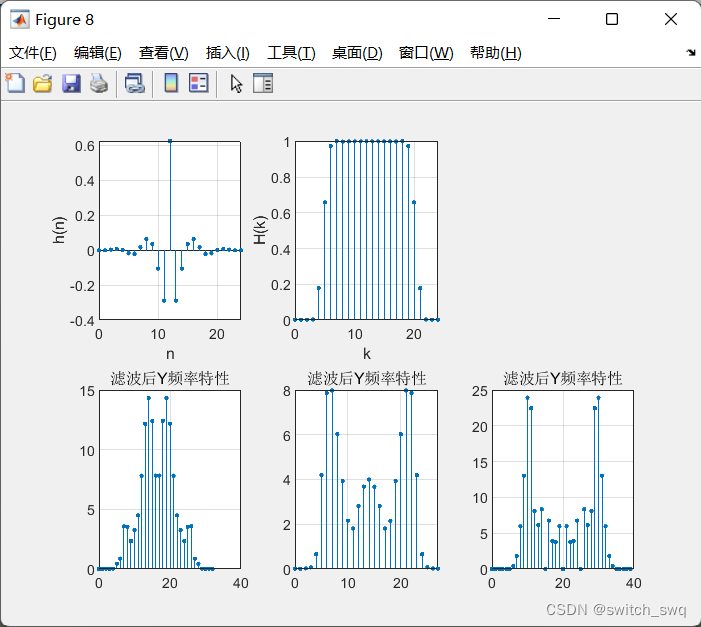
Hk=fft(hn,length(hn));
<3>绘图
%   滤波结果
y1=conv(hn,x1);
y2=conv(hn,x2);
y3=conv(hn,x3);
n1=length(y1);
n2=length(y2);
n3=length(y3);
Y1=fft(y1,n1);
Y2=fft(y2,n2);
Y3=fft(y3,n3);
%   绘图
figure;
subplot(2,3,1);
stem(0:Nn-1,hn,'.');
xlabel('n');
ylabel('h(n)');
grid on
subplot(2,3,2);
stem(0:Nn-1,abs(Hk),'.');
xlabel('k');
ylabel('H(k)');
grid on
subplot(2,3,4);
stem(0:n1-1,abs(Y1),'.');
title('滤波后Y频率特性');
grid on
subplot(2,3,5);
stem(0:n2-1,abs(Y2),'.');
title('滤波后Y频率特性');
grid on
subplot(2,3,6);
stem(0:n3-1,abs(Y3),'.');
title('滤波后Y频率特性');
grid on

三.实验结果

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/231081.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

2024年高效远程协同运维工具推荐

2024年高效远程协同运维工具推荐

随着企业的不断发展以及变化&#xff0c;企业的内部IT环境也是日益复杂&#xff0c;一跨高效远程协同运维工具必不可少&#xff0c;不仅可以提高生产力&#xff0c;还能降低运营成本。这里就给大家推荐2024年高效远程协同运维工具。 高效远程协同运维工具应用场景 1、IT运维管…
阅读更多...
openresty介绍、安装、使用

openresty介绍、安装、使用

openresty介绍、安装、使用 1、openresty介绍2、openresty安装3、openresty使用 1、openresty介绍 OpenResty是一个基于 Nginx 与 Lua 的高性能 Web 平台&#xff0c;其内部集成了大量精良的 Lua 库、第三方模块以及大多数的依赖项。用于方便地搭建能够处理超高并发、扩展性极…
阅读更多...
安卓端出现https请求失败(转)

安卓端出现https请求失败(转)

背景# 某天早上&#xff0c;正在一个会议时&#xff0c;突然好几个同事被叫出去了&#xff1b;后面才知道&#xff0c;是有业务同事反馈到领导那里&#xff0c;我们app里面某个功能异常。 具体是这样&#xff0c;我们安卓版本的app是禁止截屏的&#xff08;应该是app里做了拦…
阅读更多...
设计模式（三）-结构型模式（2）-桥接模式

设计模式（三）-结构型模式（2）-桥接模式

一、为何需要桥接模式&#xff08;Bridge&#xff09;? 在软件设计中&#xff0c;存在有两个或多个不同维度的模块时&#xff0c;我们需要将这些模块使用到在一起&#xff0c;来实现一个完整的功能。所谓不同维度的意思就是这些模块所负责的职责是不同的&#xff0c;并且它们…
阅读更多...
lua安装

lua安装

lua安装 1.Lua介绍 特点&#xff1a;轻量、小巧。C语言开发。开源。 设计的目的&#xff1a;嵌入到应用程序当中&#xff0c;提供灵活的扩展和定制化的功能。 luanginx&#xff0c;luaredis。 2.windows安装lua windows上安装lua&#xff1a; 检查机器上是否有lua C:\U…
阅读更多...
【《漫画算法》笔记】找数组中出现奇数次的元素

【《漫画算法》笔记】找数组中出现奇数次的元素

给定数组&#xff0c;只有一个元素出现过奇数次 思路&#xff1a; 考虑到异或运算的性质——两个等值数的异或结果等于0&#xff0c;两个不等值的数异或结果为1&#xff0c; 将给定数组的所有元素异或起来&#xff0c;最终结果就是那个“唯一出现过计数次”的数。 给定数组&a…
阅读更多...
10129 - Play on Words （UVA）

10129 - Play on Words （UVA）

题目链接如下&#xff1a; Online Judge 欧拉道路的题。 有向图满足欧拉道路有两个条件&#xff1a;1&#xff0c;图是连通的&#xff08;无向边意义上&#xff09;&#xff1b;2&#xff0c;最多只能有两个点的出度不等于入度&#xff0c;而且其中一个点的出度比入度大1&am…
阅读更多...
Kubernetes 的用法和解析 -- 4

Kubernetes 的用法和解析 -- 4

一.Deployment 资源详解 如果Pod出现故障&#xff0c;对应的服务也会挂掉&#xff0c;所以Kubernetes提供了一个Deployment的概念 &#xff0c;目的是让Kubernetes去管理一组Pod的副本&#xff0c;也就是副本集 &#xff0c;这样就能够保证一定数量的副本一直可用&#xff0c;…
阅读更多...
概率论复习

概率论复习

第一章&#xff1a;随机概率及其概率 A和B相容就是 AB 空集 全概率公式与贝叶斯公式&#xff1a; 伯努利求概率&#xff1a; 第二章&#xff1a;一维随机变量及其分布&#xff1a; 离散型随机变量求分布律&#xff1a; 利用常规离散性分布求概率&#xff1a; 连续性随机变量…
阅读更多...
华为OD试题四（字符串统计、计算误码率、计算最大乘积）

华为OD试题四（字符串统计、计算误码率、计算最大乘积）

1. 字符串统计 题目描述&#xff1a; 给定两个字符集合&#xff0c;一个为全量字符集&#xff0c;一个为已占用字符集。 已占用的字符集中的字符不能再使用&#xff0c;要求输出剩余可用字符集。 输入描述&#xff1a; 1、输入为一个字符串&#xff0c;一定包含符号。前的为全…
阅读更多...
记录每日LeetCode 746.使用最小花费爬楼梯 Java实现

记录每日LeetCode 746.使用最小花费爬楼梯 Java实现

题目描述&#xff1a; 给你一个整数数组 cost &#xff0c;其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用&#xff0c;即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 请你计算并返回达到楼梯顶部的最低…
阅读更多...
Windows使用VNC Viewer远程桌面Ubuntu【内网穿透】

Windows使用VNC Viewer远程桌面Ubuntu【内网穿透】

文章目录 前言1. ubuntu安装VNC2. 设置vnc开机启动3. windows 安装VNC viewer连接工具4. 内网穿透4.1 安装cpolar【支持使用一键脚本命令安装】4.2 创建隧道映射4.3 测试公网远程访问 5. 配置固定TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址5.3 测试…
阅读更多...
hypervisor display显卡节点card0生成过程

hypervisor display显卡节点card0生成过程

ditsi 配置 lagvm/LINUX/android/vendor/qcom/proprietary/devicetree/qcom direwolf-g9ph.dts #include "direwolf-vm-la.dtsi" direwolf-vm-la.dtsi #include "display/quin-vm-display-la.dtsi" quin-vm-display-la.dtsi //对应/sys/class/drm/card…
阅读更多...
推荐几款值得收藏的3DMAX插件

推荐几款值得收藏的3DMAX插件

推荐几款值得收藏的3DMAX插件 StairGenerator StairGenerator一键楼梯插件&#xff0c;不需要花费太多的时间&#xff0c;轻松从2D平面图生成3D楼梯模型&#xff0c;生成的楼梯模型细节丰富真实。 【主要功能】 1.简单&#xff1a;轻松实现2D到3D建模。 2.具有最详细三维结…
阅读更多...
高级桌面编程（一）

高级桌面编程（一）

前言 学习心得&#xff1a;C# 入门经典第8版书中的第15章《高级桌面编程》 创建控件并设置样式 1 样式 Style WPF 当中我们可以对每一个控件进行完全的自定义。我们可以随意更改控件外观和功能。提供我们能完成这样的效果与控件的样式&#xff08;Style&#xff09;有着不可分…
阅读更多...
【mysql8的一个利器, CTE查询】

【mysql8的一个利器, CTE查询】

今天因为一个比较头疼的mysql查询问题, 去Stack Overflow提问, 然后底下有人答复说既然用了mysql8, 不要用子查询, 直接用CTE查询. CTE查询是啥, 我直接百度了下, 然后发现, 这玩意太好用了, 但是说实话, 我可以肯定大多数人基本都不会去了解这些新出的功能,毕竟经手的项目大多…
阅读更多...
人工智能革命：共同探索AIGC时代的未来

人工智能革命：共同探索AIGC时代的未来

一、引言 随着大数据和强大的计算能力的兴起&#xff0c;人工智能技术&#xff08;AI&#xff09;正在快速发展&#xff0c;并为各个领域带来革命性的变化。人工智能与智能计算技术&#xff08;AIGC&#xff09;的融合不仅为企业、科研机构和普通用户提供了巨大的机遇&#xff…
阅读更多...
60.Sentinel源码分析

60.Sentinel源码分析

Sentinel源码分析 1.Sentinel的基本概念 Sentinel实现限流、隔离、降级、熔断等功能&#xff0c;本质要做的就是两件事情&#xff1a; 统计数据&#xff1a;统计某个资源的访问数据&#xff08;QPS、RT等信息&#xff09; 规则判断&#xff1a;判断限流规则、隔离规则、降级规…
阅读更多...
数字孪生Web3D智慧机房可视化运维云平台建设方案

数字孪生Web3D智慧机房可视化运维云平台建设方案

前言 进入信息化时代&#xff0c;数字经济发展如火如荼&#xff0c;数据中心作为全行业数智化转型的智慧基座&#xff0c;重要性日益凸显。与此同时&#xff0c;随着东数西算工程落地和新型算力网络体系构建&#xff0c;数据中心建设规模和业务总量不断增长&#xff0c;机房管理…
阅读更多...
函数装饰器基础

函数装饰器基础

1 函数装饰器基础 1.1 函数调用 描述 根据之前文章《python函数属性和注解》得知&#xff0c;python函数定义时生成函数对象并赋值给了函数名。 调用方式&#xff1a; &#xff08;1&#xff09;直接调用方式为&#xff1a;通过函数名圆括号()调用函数&#xff0c;比如f1(…
阅读更多...
最新文章

Copyright @ 2022~2023