滑动窗口（一）

滑动窗口

什么是滑动窗口算法？通俗的来讲就是 “同向双指针” ，当一组数据的规律含有单调性的时候，就可以使用下面这套逻辑来优化暴力解法。

当两个指针同向移动的时候，类似于一个窗口在滑动。使用于在连续序列里找特殊的子串、子数列、子数组等。

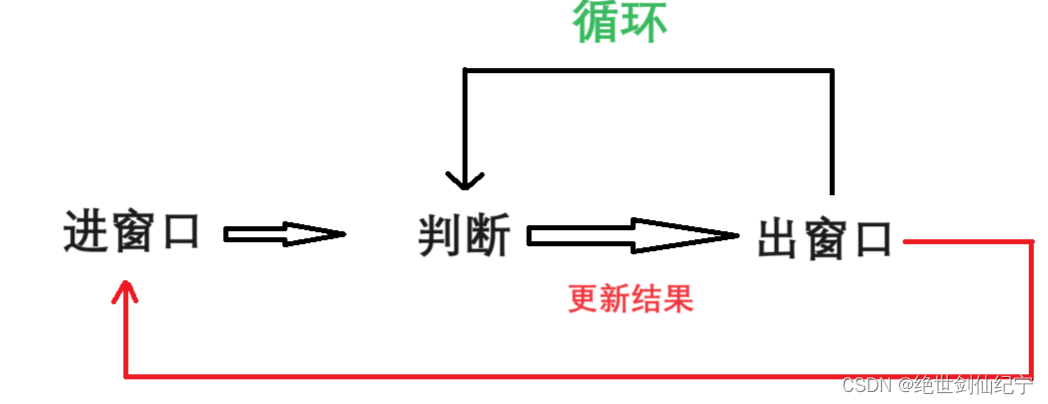
下面将用一道题来解释上面的逻辑。

长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

定义两个指针 left，right，都从零位置开始，用 sum 记录子数组的和。

第一步：进窗口（sum+=nums [right] ），将第一个值添加到 sum 中。

第二步：判断：sum 是否大于等于题目要求的 target ，如果符合，就进入循环：更新长度最小长度 len，让‘窗口’向右划（left左移）！再次进行第二步的判断，当不满足 sum 大于等于 target 这个要求的时候，就让 right++，准备下次的进窗口。

这道题还有一个细节需要注意：需要定义一个 flag 如果 满足过sum大于等于 就要让 flag 的值改变，只要当他满足过的时候，才能返回 len，否则就是序列中没有满足条件的，返回 0。

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int left = 0, right = 0, n = nums.size();int sum = 0;int len = nums.size();int flag = 0;while (right < n){    sum += nums[right];while(sum >= target){flag = 1;if (right - left < len) len = right - left + 1;sum -= nums[left];left++;}right++;}if(flag == 1) return len;else return 0;}
};

无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长连续子字符串 的长度。

思路：利用哈希表作为判断字符是否重复的依据，使用滑动窗口更新最长的长度。

因为数据比较少，所以可以直接使用 ASCII 来构建哈希表，将ASCII 当做下标，出现了的话那个位置的数就加1.

判断条件为：hash 表里 right 位置的值大于1，说明有重复的字符进入了哈希表，然后开始出窗口，循环出，直至这个 hash 表里 right 位置的值等于1后，right++，为下一次进窗口做准备。

class Solution {
public:int lengthOfLongestSubstring(string s) {int left = 0,right = 0,n=s.size();int len = 0;int hash[128]={0};while(right < n){hash[s[right]]++;while(hash[s[right]]>1){hash[s[left++]]--;}len = max(len, right -left + 1);right++;}return len;}
};

最大连续1的个数

最大连续1的个数 III

给定一个二进制数组 nums 和一个整数 k，如果可以翻转最多 k 个 0 ，则返回 数组中连续 1 的最大个数 。

此题如果采用正常方法的话，将是特别特别难的一道题，所以采用正难则反的思想。

将题目中找反转不大于K个0后的连续1的最大个数，转化为：找最长的子数组，其中这个子数组中 0 的个数不大于 K，利用滑动指针来解决就可以了，判断条件就是子数组中 0 个数小于等于 K，更新的结果就是这个子数组的长度！

class Solution {
public:int longestOnes(vector<int>& nums, int k) {//题目转化为在数组中找到一个子数组，里面零的个数小于 K 个int left = 0, right = 0, zero = 0;int n = nums.size();int len = 0;while (right < n){if(nums[right]==0) zero++;while (zero > k){if (nums[left] == 0) zero--;left++;}len = max(len, right - left+1);right++;}return len;}
};