学习目标:
动态规划五部曲:
① 确定dp[i]的含义
② 求递推公式
③ dp数组如何初始化
④ 确定遍历顺序
⑤ 打印递归数组 ---- 调试
引用自代码随想录!
60天训练营打卡计划!
学习内容:
392. 判断子序列
这个题目就是 1143.最长公共子序列 的变种,最后只需要判断最长公共子序列长度 与 s字符串(给定字符串 s 和 t ,判断 s 是否为 t 的子序列。)长度的关系。
- 动态规划五步曲:
① 确定dp[i][j]的含义 : 在[0, i] 和 [0, j]范围中的最长公共子序列的长度。(指的就是第一行第一列全填充为空,即多申请这么多空间)
② 求递推公式 :
当前行列元素相等:dp[i+1][j+1] = dp[i][j]
当前行列元素不相等:dp[i+1][j+1] = max(dp[i][j+1],dp[i+1][j]) – 从前一个元素继承公共序列长度
③ dp数组如何初始化 : 第一行和第一列都为零。空置。
④ 确定遍历顺序 : 从上到下,从左到右
class Solution {public boolean isSubsequence(String s, String t) {int size1 = s.length();int size2 = t.length();int[][] dp = new int[size1+1][size2+1];// 初始化for(int i = 0; i < size1; i++){for(int j = 0; j < size2; j++){if(s.charAt(i) == t.charAt(j)) dp[i+1][j+1] = dp[i][j] + 1;else dp[i+1][j+1] = Math.max(dp[i+1][j], dp[i][j+1]);}}return dp[size1][size2] == size1;}
}
115.不同的子序列
- 动态规划五步曲:
① 确定dp[i][j]的含义 : 以 i-1 为结尾的 s 中有以 j-1 为结尾的 t 的个数。(指的就是第一行和第一列都置为空)
② 求递推公式 : (不是很好理解)
当前行列元素相等:dp[i+1][j+1] = dp[i][j] + dp[i][j+1] – 目标字符串是拼凑成的序列的数量 + 目标字符串是连续子序列的数量
当前行列元素不相等:dp[i+1][j+1] = dp[i][j+1] – 目标字符串是连续子序列
(精髓)以下图为例分析上述的递推公式:
其中s为ba时,t为babgba。因为此时行列元素相等,所以递推公式为dp[i+1][j+1] = dp[i][j] + dp[i][j+1] ,其中dp[i][j]代表的是babgba有几个b,dp[i][j+1]代表出现了几次完整的ba字符串,此时s[ ]为a,所以babgba中的所有ba字符串可以由2种方式组成,一种是连续的ba字符串,另一种是分散的b加上当前s[ ]的最后一位a,所以共计有4种。正好可以对应递推公式。
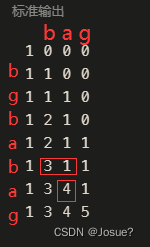
③ dp数组如何初始化 : 第一列为1,第一行除dp[0][0]外都为0。因为列长是目标字符串长度,第一列为空字符,所以第一列为1。
④ 确定遍历顺序 : 从上到下,从左到右
class Solution {public int numDistinct(String s, String t) {int s_size = s.length();int t_size = t.length();int[][] dp = new int[s_size+1][t_size+1];// 初始化// Arrays.fill(dp[0], 1);for (int i = 0; i < s.length() + 1; i++) {dp[i][0] = 1;}for(int i = 0; i < s_size; i++){for(int j = 0; j < t_size; j++){if(s.charAt(i) == t.charAt(j)) dp[i+1][j+1] = dp[i][j] + dp[i][j+1];else dp[i+1][j+1] = dp[i][j+1];}}// for(int i[]: dp){// for(int j : i)// System.out.print(j + " ");// System.out.println(" ");// }return dp[s_size][t_size];}
}学习时间:
- 上午两个半小时,整理文档半小时。

)






)


)
:自由切换图表的背景颜色)

 11)




