【数据结构】八大排序之希尔排序算法

🦄个人主页:修修修也

🎏所属专栏:数据结构

⚙️操作环境:Visual Studio 2022

一.优化直接插入排序算法

我们在之前对直接插入排序算法的优化部分通过对直接插入排序的分析可以得到一个结论,即:

进行直接插入排序的数组,如果越接近局部有序,则后续进行直接插入排序算法时其时间复杂度就会越低.

所谓基本有序,就是指小的关键字基本在前面,大的关键字基本在后面,而不大不小的基本在中间.

例如下面这个数组序列,虽然它还是无序的状态,甚至是局部逆序的状态,但至少它的前8个数据"0-7"都在前半部分,后8个数据"8-15"都在后半部分,这样就比完全逆序状态更接近基本有序,相应的算法执行的次数也直接减少了一半:

当我们再进一步,将它们整合的更加接近局部有序一些,可以发现,这时算法的总执行次数又直接减少了一半:

而当我们整合到最接近局部有序时,可以发现,这时算法的总执行次数表达式中的n^2项就已经消失了:

我们已经知道了如果将数组整合成局部有序,就可以大大优化直接插入排序,问题是如何通过预排序将数列整合成局部有序呢?

其实很简单,我们将这些数字不断分为gap组,然后分别让相隔gap个元素的一组数据保持有序就可以了:

如下,第一次我们将数组分为8组,然后使相隔8个元素的每组数据都保持有序,即第一组数据"15和7"要调整为顺序,则将其二者调换位置即可,后续七组操作同理:

然后我们就可以得到如下数组了:

接着,我们再将数组分为4组,让每隔4个元素的数据保持有序,即第一组数据"7,3,15,11"要调整为顺序,则将其看作一个代排数组,然后用直接插入排序将其调整为"3,7,11,15"的顺序,后面7组同理:

然后我们就可以得到如下数组:

我们继续再将数组分为2组,让每隔2个元素的数据保持有序,即将第一组数据"3,1,7,5,11,9,15,13"直接插入排序,将其调整为"1,3,5,7,9,11,13,15"的顺序,第二组同理:

然后我们就可以得到如下数组:

然后就是最后一步,我们将数组看作一组,让相邻的两个元素的数据保持有序,即将全组数据直接插入排序,就可以得到最终结果:

至此,其实我们对直接插入排序的优化过程,就是希尔排序算法的思路.

二.希尔排序简介及思路

希尔排序(Shell Sort)是一种插入排序算法.

它的基本思想是:

先选定一个整数,把待排序文件中所有数据分成gap个组,所有距离为gap的数据分在同一组内,并对每一组内的数据进行排序.
重复上述分组和排序的工作,当达到gap=1时,所有数据在统一组内排好序.

算法动图演示如下:

三.希尔排序算法的代码实现

算法实现步骤:(以升序为例)

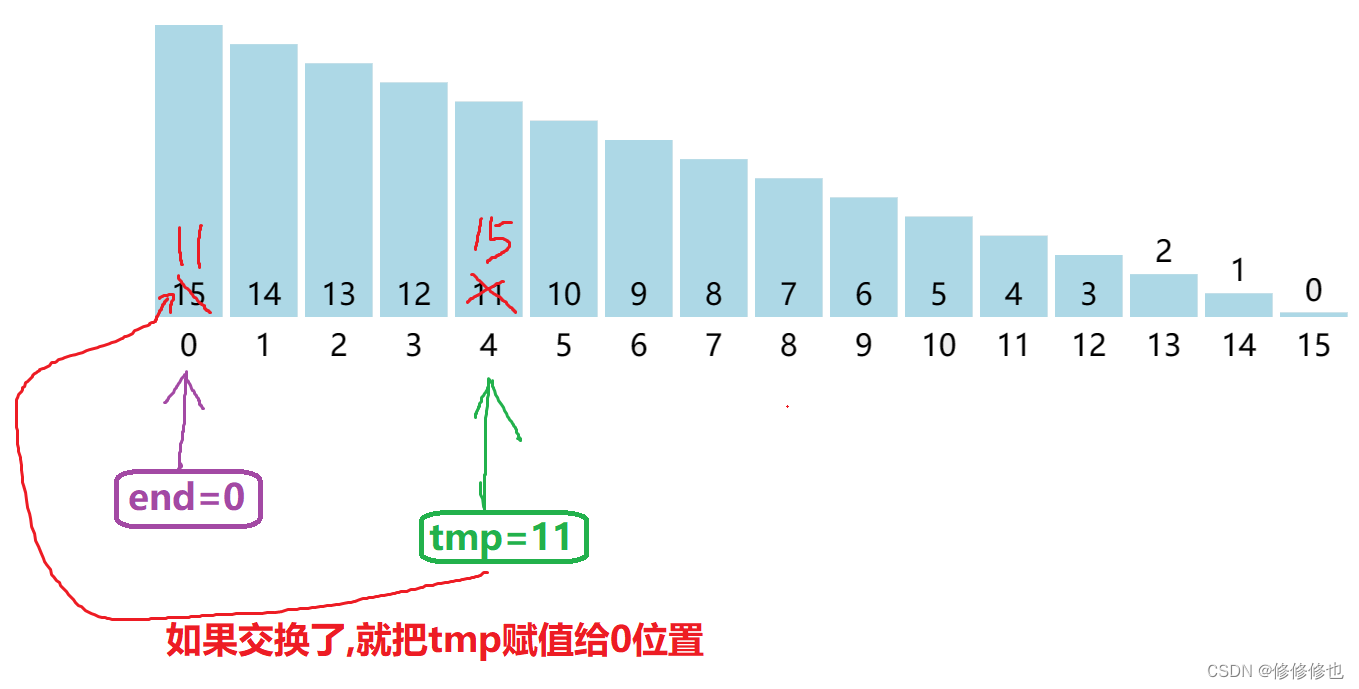
从下标为0的元素开始,遍历到下标为n-gap个元素为止,我们使用end来记录本次处理的元素下标,用tmp记录下间隔gap的元素的数值.
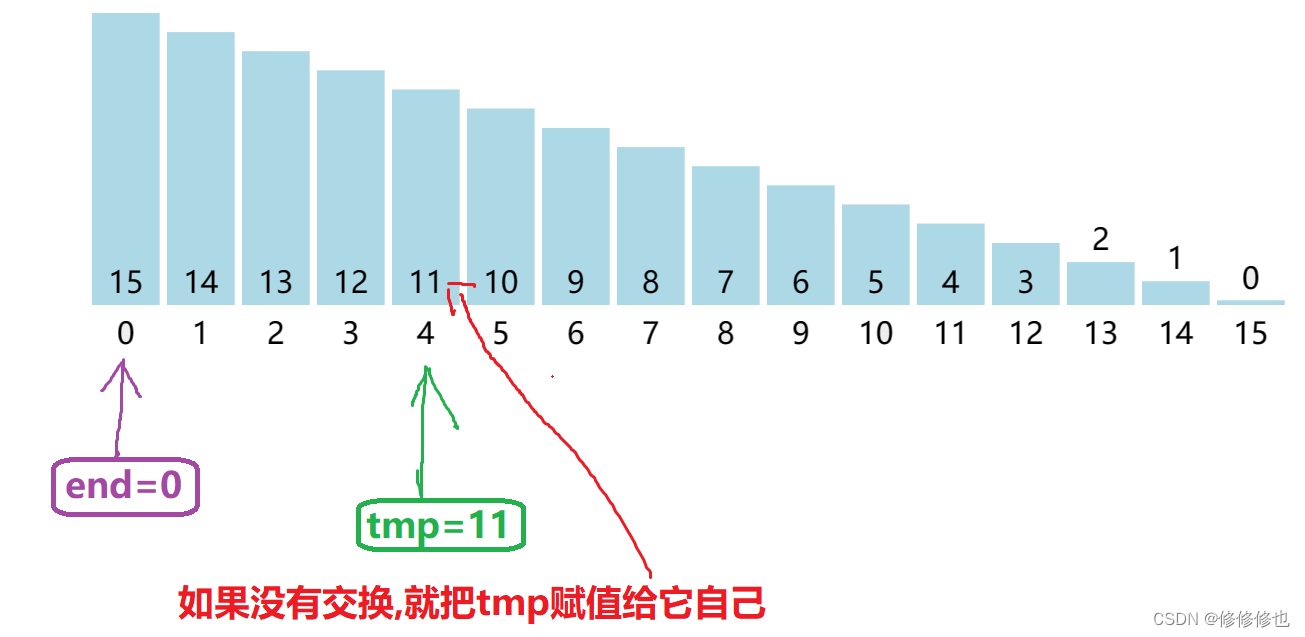
和间隔gap的两个元素进行比较,如果a[end+gap] < a[end],则将a[end]的值赋值给a[end+gap],并给end减掉gap.
然后无论这次有没有交换位置,都将tmp赋值给a[end+gap]的位置,如果没有交换,则a[end+gap]就是tmp原本的值,如果这次有交换,则因为end减去了gap,则会使tmp赋值给原本a[end]的位置.该部分图示如下:
当第一轮遍历完下标为n-gap的元素之后,给gap除以2,继续重复1-3步的操作.
不断重复第4步操作,直到最终gap为1,即执行直接插入排序后,本次排序完成.

搞清算法实现步骤后,代码实现就比较简单了,希尔排序代码如下:

//希尔排序(升序
void ShellSort(int* a, int n)
{int gap = n;//gap>1都是在预排序//gap==1时就是直接插入排序了while (gap > 1){gap /= 2;//嫌慢的话可以gap/=3+1.加一是要保证最后一次一定是1for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

四.希尔排序算法的时间复杂度分析

希尔排序的时间复杂度的计算是较为复杂的,我们先来看两本官方书籍对该部分的描述:

       希尔排序的分析是一个复杂的问题，因为它的时间是所取“增量”序列的函数，这涉及一些数学上尚未解决的难题。因此，到目前为止尚未有人求得一种最好的增量序列，但大量的研究已得出一些局部的结论。如有人指出，当增量序列为 $dlta[k]=2^{t-k+1}-1$ 时，希尔排序的时间复杂度为 $O(n^{\frac{3}{2}})$ ，其中t为排序趟数， $1 \leqslant k \leqslant t \leqslant \left \lfloor log_{2}(n+1) \right \rfloor$ 。

        还有人在大量的实验基础上推出：当n在某个特定范围内，希尔排序所需的比较和移动次数约为 $n^{1.3}$ ，当 $n\rightarrow \infty$ 时，可减少到 $n((log_{2}n)^{2})^{2}$ 。增量序列可以有各种取法，但需注意：应使增量序列中的值没有除1之外的公因子，并且最后一个增量值必须等于1。

                                                                 ——《数据结构(C语言版)》严蔚敏

gap的取法有多种。最初Shell提出取 $gap=\left \lfloor \frac{n}{2} \right \rfloor$ ， $gap=\left \lfloor \frac{gap}{2} \right \rfloor$ ，直到gap=1,后来Knuth提出取 $gap=\left \lfloor \frac{gap}{3} \right \rfloor+1$ 。还有人提出都取奇数为好，也有人提出各gap互质为好。无论哪一种主张都没有得到证明。
对希尔排序的时间复杂度的分析很困难，在特定情况下可以准确地估算关键码的比较次数和对象移动次数，但想要弄清关键码比较数和对象移动次教与增量选择之间的依赖关系，并给出完整的数学分析，还没有人能够做到。在Knuth所著的《计算机程序设计技巧》第3卷中，利用大量的实验统计资料得出，当n很大时，关键码平均比较次数和对象平均移动次数大约在 $n^{1.25}$ 到 $1.6n^{1.25}$ 范围内，这是在利用直接插入排序作为子序列排序方法的情况下得到的。 ——《数据结构-用面向对象方法与C++描述》殷人昆

因此,当前对于希尔排序的时间复杂度,学术界仍没有一个确切的研究结果,我们只能在估算希尔排序时间复杂度时借助Knuth大佬的实验统计结果,即采用 $O(n^{1.25})$ 到 $O(1.6*n^{1.25})$ 来近似的估算希尔排序的时间复杂度.

结语

希望这篇希尔排序算法详解能对大家有所帮助,欢迎大佬们留言或私信与我交流.

有关更多排序相关知识可以移步:

【数据结构】八大排序算法https://blog.csdn.net/weixin_72357342/article/details/135038495?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135038495%22%2C%22source%22%3A%22weixin_72357342%22%7D&fromshare=blogdetail学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!