八数码原题
剖析一下BFS
BFS算法是一种图遍历算法,它从起点开始,逐层扩展搜索范围,直到找到目标节点为止。
BFS算法一般选择队列作为节点存储的数据结构,我们将搜索目标节点的问题抽象为寻找目标状态,那么队列存储的对象就是每一种状态。
对于状态的含义与变化过程,BFS算法如下要求(为了讲解得更加透彻,举走迷宫问题为例):
- 初始以及其拓展出开的状态都要存储在队列中。在走迷宫问题中,队列q存储已走过的点 ,点代表位置状态,基于一个点可以拓展出它四周的点;
- 问题的求解必须有初始状态与最终状态。在走迷宫问题中,起点(0,0)便是初始状态,而终点(n,n)是最终状态;
- 问题的状态次数是有限的,已出现的状态一般需要被记录下来。在走迷宫问题中,dis[i][j]表示从起点到达点(i,j)的距离。当dis的所有元素被初始化为0时,如果dis[i][j]非零时,就说明点(i,j)已被记录过;
- 当前状态preState可以拓展出其他状态State,如果State已经出现过或者不符合要求,那么该状态无法加入队列中.
八数码问题的求解
问题描述
八数码,在3×3的方格棋盘上,摆放着1到8这八个数码,有1个方格放置字符x,其初始状态如图所示,要求对字符x执行x左移、x右移、x上移和x下移这四个操作使得棋盘从初始状态到目标状态。
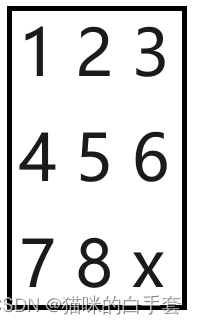
基于上述状态能够拓展出如下四种状态:

八数码问题要求是,对字符x进行若干次唯一操作,得到目标状态并且求算操作次数:

求解思路
- 每一个矩阵的里面的元素能够用一个字符串来存储,例如存储最终状态string s = "12345678x";
- 本问题借助state结构体存储每一种状态,state的分量为:s,pos,step.其中,s代表该状态对应的字符串,pos代表x在s字符串中的位置,step代表本状态由初始转台经过了step次操作得来;
- 定义一个map<string,bool>st映射,记录该字符串(即新拓展出来的状态)曾经是否出现过,即已出现的状态需要被记录下来;
- 当前状态preState包含三个分量{s,pos,step},根据pos与s值,拓展出其他至多四种状态,具体实现将代码的genOtherState函数.
好啦,大功告成~~👌👌👌其他细节部分见代码后,也许会有更加深刻的体会(代码有详细注释,所谓优秀的代码本身就是学习文档!!!)
代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<string>
#include<map>
#include<queue>
using namespace std;// come from Acwing// 记录状态
struct state {string s;int pos; // x的位置int step; // step次交换
};string str;
map<string, bool>st; // 记录某个状态是否曾出现
queue<state>q; // 状态队列// 产生其他状态
void genOtherState(const state& sta) {string s;state t;// 判断是否能够交换x与它上面字符的位置if (sta.pos - 3 >= 0) {// 交换两个字符的位置s = sta.s;swap(s[sta.pos], s[sta.pos - 3]);if (!st[s]) {q.push(state{ s,sta.pos - 3,sta.step + 1 });st[s] = true;}}// 判断是否能够交换x与它下面字符的位置if (sta.pos + 3 <= 8) {s = sta.s;swap(s[sta.pos], s[sta.pos + 3]);if (!st[s]) {q.push(state{ s,sta.pos + 3,sta.step + 1 });st[s] = true;}}// 判断是否能够交换x与它右边字符的位置if (sta.pos % 3<=1) {s = sta.s;swap(s[sta.pos], s[sta.pos + 1]);if (!st[s]) {q.push(state{ s,sta.pos + 1,sta.step + 1 });st[s] = true;}}// 判断是否能够交换x与它左边字符的位置if (sta.pos % 3 >= 1) {s = sta.s;swap(s[sta.pos], s[sta.pos - 1]);if (!st[s]) {q.push(state{ s,sta.pos - 1,sta.step + 1 });st[s] = true;}}
}int bfs(int pos) {string target = "12345678x"; // 目标状态// 初始化state init = state{ str,pos,0 };q.push(init);st[str] = true;while (q.size()) {auto t = q.front(); // 取出队头状态进行拓展q.pop();if (t.s == target) {return t.step;}// 当前状态拓展出其余状态genOtherState(t);}return -1;
}int main() {int cnt = 9;int pos = 0;// 输入for (int i = 0;i <= 8;i++) {char a;cin >> a;if (a == 'x') {pos = i;}str += a;}int res = bfs(pos);cout << res << endl;return 0;
}总结
本博客先解释了BFS的存储队列节点的抽象含义,将每一个节点看作一种状态,并从状态存储、状态记录、状态拓展等角度解答了BFS算法如何解决遍历问题。
紧接着,我们借助BFS算法的状态处理方法给出了八数码问题的求解思路。我们以字符串存储了八数码的每一种状态,每一种状态记录{s,pos,step}三个分量,借助st映射记录新拓展出的状态,并于代码中给出状态拓展的方法。
实际上,八数码问题只是抽象BFS问题的一种实例化,当我们判断一个问题是否属于BFS问题时,需要判断问题是否存在初始状态与最终状态?每一种状态如何存储,有哪些分量?如何记录每一种状态?每一种状态拓展出其他状态的方式是否是规律的且有限的?掌握了如上的思考方式,相信你能够在下一次遇到或判断一个问题是否属于BFS问题时,你能够更加游刃有余!!!

:最短路问题)






 以及常见的色调)





)
:ACL与NAT)



