题目链接:
https://ac.nowcoder.com/acm/contest/72041#question
A题
解题思路
签到
代码
#include <bits/stdc++.h>
using namespace std;int main() {int a, b, c, d, e;cin >> a >> b >> c >> d >> e;int A, B, C, D;cin >> A >> B >> C >> D;if (a * A + b * B + c * C - d * D > e)cout << "YES\n";elsecout << "NO\n";return 0;
}
B题
解题思路
贪心,很显然,我们应该尽可能将更大的魔法1用于更大的魔法2。
所以先将两个数组从大到小排序。
一个小细节是:如果当前直接使用魔法2就能击败,那么就直接使用魔法2,没必要先使用魔法1。以及如果当前魔法1是1,那么也没必要使用。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e4 + 10;
int a[maxn], b[maxn];void solve() {int n, m, x;cin >> n >> m >> x;for (int i = 1; i <= n; i++) {cin >> a[i];}for (int i = 1; i <= n; i++) {cin >> b[i];}sort(a + 1, a + 1 + n, greater<int>());sort(b + 1, b + 1 + n, greater<int>());int cnt = 0, i = 1, j = 1;while(j <= n) {int f1 = a[i] * b[j];int f2 = b[j];if (f1 > f2 && x > f2) {cnt += 2;x -= f1;i++;j++;} else {cnt++;x -= f2;j++;}if (x <= 0)break;}if (x <= 0)cout << cnt << "\n";elsecout << -1 << "\n";
}int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout << fixed;cout.precision(18);solve();return 0;
}
C题
解题思路
看见题面是Minecraft MITE直接肃然起敬。
根据题意很容易分析出,只有三种方案可以做出铜镐:
1、16个铜粒。
2、12个铜粒+4个银粒。
3、12个铜粒+4个金粒。
将三种方案的概率相加即可。
公式如下:
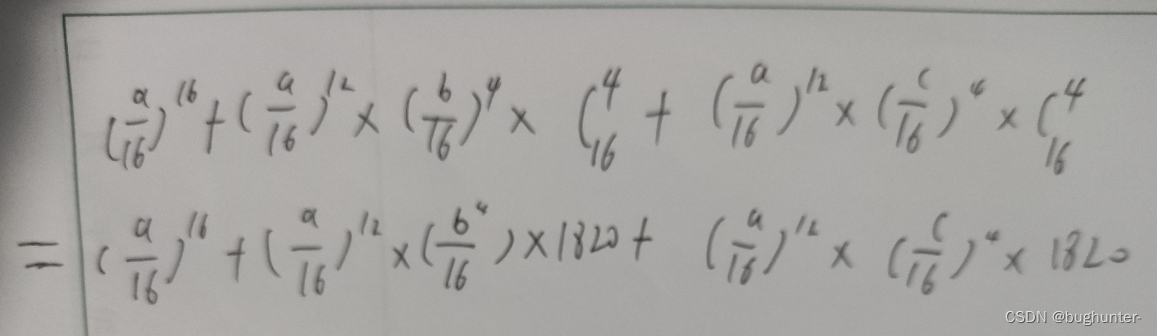
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e4 + 10;
//double PJIN[20], PYIN[20], PTONG[20];double pow(double b, int e) {if (e == 0)return 1;if (e == 1)return b;double res = pow(b, e / 2);if (e % 2 == 0) {return res * res;}else {return res * res * b;}
}
double Power(double base, int exponent) {if (exponent == 0)return 1;if (exponent == 1)return base;if (exponent < 0) {return pow(1 / base, -exponent);}else {return pow(base, exponent);}}void solve() {double a, b, c;cin >> a >> b >> c;double pTong = a / 16;double pYin = b / 16;double pJin = c / 16;double tongGao = Power(pTong, 12);// 方案一:4铜粒(工作台) + 12铜粒(一个铜稿子)double f1 = Power(pTong, 4) * tongGao;// 方案二:4银粒(工作台) + 12double f2 = Power(pYin, 4) * tongGao * 1820; // C(16, 4) = 1820// 方案三:4金粒 + 12double f3 = Power(pJin, 4) * tongGao * 1820;cout << (f1 + f2 + f3) << "\n";
}int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout << fixed;cout.precision(18);int t;cin >> t;while (t--)solve();return 0;
}
D题
解题思路
n <= 500,所以O(n^3)也是能过的。
考虑找出左端点为ch1,右端点为ch2,长度为k的子序列数量,假设有si == ch1,sj == ch2,那么[i, j]这段子串对于答案的贡献为C(j - i - 1, k - 2)。
因为这相当于在固定了si和sj的情况下,在中间j - i - 1个字符([i + 1, j - 1]这个子串)中选择k - 2个字符。
我们可以考虑先预处理出答案,暴力枚举,第一层循环枚举左端点,第二层循环枚举右端点,第三层循环枚举子序列长度,统计出数量。对于组合数我们可以先用杨辉三角预处理出来。
详见代码和注释。
代码
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 5e2 + 10;
const int INF = 0x3fffffff;
const ll mod = 998244353;
ll c[maxn][maxn];
string s;
int n;
ll ans[300][maxn][maxn]; // 预处理答案,ans[ch1][ch2][k]代表在字符串s中左端点为ch1,右端点为ch2,长度为k的子序列的数量void initC() {for (int i = 0; i <= n; i++) {c[i][i] = 1;c[i][0] = 1;}for (int i = 1; i <= n; i++) {for (int j = 1; j < i; j++) {c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;}}
}void init() {// 用杨辉三角预处理组合数initC();// 预处理for (int i = 0; i < n; i++) { // 枚举左端点for (int j = i + 1; j < n; j++) { // 枚举右端点for (int k = 2; k <= j - i + 1; k++) { // 枚举序列长度char ch1 = s[i];char ch2 = s[j];// 当左端点为i右端点为j,能贡献出C(j - i - 1, k - 2)个长度为k的左端点si,左端点sj的子序列ans[ch1][ch2][k] += c[j - i - 1][k - 2]; // 将贡献数量加到对应的答案记录ans[ch1][ch2][k] %= mod;}}}
}void solve() {cin >> n;cin >> s;// 预处理init();// 询问查询int m;cin >> m;while (m--) {char ch1, ch2;cin >> ch1 >> ch2;int len;cin >> len;cout << ans[ch1][ch2][len] << endl;}
}int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout << fixed;cout.precision(18);solve();return 0;
}




)









导入坐标点txt)
)



