初级数据结构（五）——树和二叉树的概念

文中代码源文件已上传：数据结构源码

<-上一篇初级数据结构（四）——队列 | NULL 下一篇->

1、树结构（Tree）

1.1、树结构的特点

自然界中的树由根部开始向上生长，随机长出分支，分支之上又可长出分支，层层递进，直至长出叶子则此分支结束。

数据结构中“树”的概念便是借鉴大自然中的树，将下图垂直镜像翻转便是如此，只是在画结构图时往往更习惯由上向下画。它从根节点开始不断长出分支，直至终端。与自然中的树不同点在于，随着数据后续插入，树结构的叶子节点也可能变为分支节点。

尤其需要注意，不同分支上的节点不可互相交织。下图中红色线条连接到其他分支的节点，这就不属于树结构：

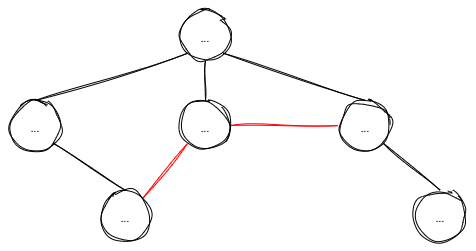
总之，树是若干个节点的有限集，有且仅有一个根节点。树的分支数量可以任意多，也可以不包含分支仅有一个根节点甚至没有节点（没有节点的树称为空树）。不同分支的节点互不相交。

1.2、常用名词

在了解树结构特点的同时，为了后续使用该结构时方便描述，还应了解几个名词。

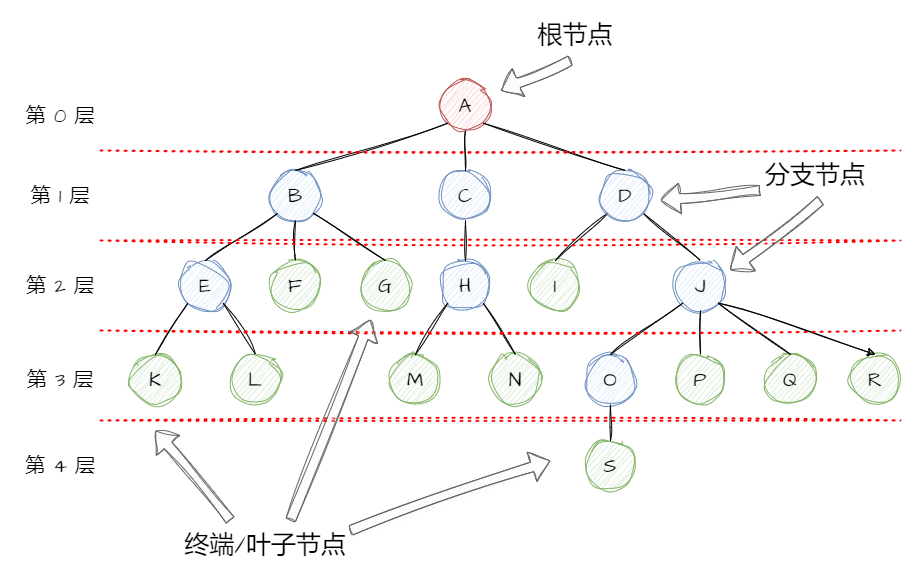
节点（ Node ）：树中的每一个元素称为节点，上图中每个圆圈都代表一个节点；

根节点（ Root ）：最初的节点称为根节点，如上图中的 A ；

子树（ Subtree ）：每个节点除开自身，将下一级节点当作新的根节点，从新的根节点往下所有节点的集合称为该节点的子树。上图中 B 及往后的节点是 A 的子树， F 又是 B 的子树（所以树是递归结构）；

分支节点（ Branch ）：能够延申出其他节点的节点（度不为 0 的节点）都称作分支节点，如上图中红色及蓝色标识的节点都属于分支节点；

终端节点、叶子节点（ Leaf ）：不包含任何分支节点的节点（度为 0 的节点）称为终端节点或者叶子节点。上图中绿色标识的节点属于叶子节点；

度（ Degree ）：一个节点的分支数量叫作该节点的度，如上图 E 有两个分支 K 和 L ，所以 E 的度是 2 。一棵树中所有节点的度的最大值就是这棵树的度，上图中度最大的节点是 J ，有 4 个度，所以这棵树的度也是 4 ；

层次（ Level ）：从树或者子树的顶层到最底层的顺序进行排序。在这个顺序中，每个节点都被视为位于树的某个层次上。最顶上可以视为第 0 层，也可以视作第 1 层。

深度、高度（Depth）：最大层次称为这棵树的深度或者高度。如图中的树从根节点开始向下，最多可经 A、D、J、O、S 这 5 个节点（ 5 个层次），所以这棵树的深度为 5 ；

父节点、双亲节点（ Parent ）：一个节点的上一级节点称为该节点的父节点或者双亲节点。如图中 E 是 K 的父节点，A 是 B 的父节点；

子节点（ Child ）：一个节点的下一级节点称为该节点的子节点。图中的 O、P、Q、R 都是 J 的子节点；

兄弟节点（ Sibling ）：与某个节点有同一个父节点的节点称为兄弟节点。如图 E、F 都是 G 的兄弟节点；

祖先节点（ Ancestry ）：某个节点上数若干级直到根节点，经过的这些节点都称为祖先节点。图中 A、C、H 都是 M 或者 N 的祖先节点；
子孙节点（ Descendant ）：一个节点往下的所有节点都称为该节点的子孙节点。如图中 I、J、O、P、Q、R、S 都是 D 的子孙节点；

堂兄弟节点（ Cousin ）：与某个节点同一层次除了自身和兄弟节点外其他所有节点称为该节点的堂兄弟节点。如图中 H、I、J 都是 E、F、G 的堂兄弟节点；

森林（ Forest ）：若干颗互不相交的树称为森林。图中剔除 A 节点后， B、C、D 子树则构成森林；

有序树（ Ordered Tree ）：一棵树中各子树按照一定规律排序不可互换，则称为有序树。如图中如果将这棵树的 A、B、C …… 当作一种顺序，那么可视为有序树；

无序树（ Unordered Tree ）：有序树之外的树都称作无序树。

1.3、树的存储方式

如上图的树结构，如果要在代码中定义其结构体，常规能想到的是除了定义一个储存数据的成员变量外，定义若干个子节点指针。而由于子节点的数量是不确定的，因此将其定义为数组。

typedef int DATATYPE;
typedef struct Node
{DATATYPE data;            //存储数据size_t childCount;        //子节点个数size_t capacity;          //已开辟空间大小struct Node* child[0];    //子节点指针数组
}Node;

若要找到图中 1-2-2 节点则执行：

root->child[0]->child[1]->child[1];

但这对于有序树这种不可随意交换节点位置的结构还好，如果是无序树，而且在经常需要交换节点的情况下，频繁挪动数组元素显得十分不灵活。因此，还有一种储存方式，每个节点仅储存第一个子节点和其下一个兄弟节点的指针。

在结构体创建上也显得简单，而且无需每次添加数据都检查空间：

typedef int DATATYPE;
typedef struct Node
{DATATYPE data;struct Node* sibling;struct Node* child;
}Node;

同样是找到 1-2-2 节点：

root->child->child->sibling->child->sibling;

看似更为复杂，但整个结构在增删数据或者交换数据的操作上跟之前的结构完全不是一个量级。具体过程这里就不展开赘述，实际上就是对链表和顺序表在增删数据或者交换数据操作上的区别。

2、二叉树（ Binary Tree ）

2.1、节点基本形态

二叉树是一种特殊的树，每个节点的子节点不超过 2 个，它的度最大为 2 。此外，二叉树是有序树。一般其节点的结构体类型如下：

typedef int DATATYPE;
typedef struct Node
{DATATYPE data;struct Node* left;struct Node* right;
}

因此，二叉树包含以下五种基本形态：

其中，由于二叉树是有序树，所以左分支形态和右分支形态不是同一种结构，代码的表现上也完全不同：

//空
root = NULL;
//无分支
root->left = NULL;
root->right = NULL;
//左分支
root->left = &nodeLeft;
root->right = NULL;
//右分支
root->left = NULL;
root->right = &nodeRight;
//双分支
root->left = &nodeLeft;
root->right = &nodeRight;

2.2、二叉树的特殊形态

2.2.1、斜二叉树

所有节点的左或者右节点全为空的二叉树称为斜二叉树。斜二叉树每一层有且只有一个节点，节点数等于树的深度。如图。

斜二叉树可看作是一种非环状单链表，使用上也与单链表无差异。

2.2.2、完全二叉树

如果二叉树的深度为 n ，根节点处于第 0 层，除了最底层节点，其余每一层中第 L 层节点个数 $C_{L}$ 都满足 $C_{L} = 2^{L}$ ，且底层最右侧节点满足其父节点的左子节点不为空，其堂兄弟节点的父节点度都为 2 ，则这类二叉树称为完全二叉树。如下图。

上面的描述可能有点过于抽象，可以观察图片，然后用另一种方式概括：

a、完全二叉树的叶子节点仅存在该二叉树的最底层和次底层；

b、最底层的叶子节点无空隙地紧密排列在左边部分，右边部分可以为空；

c、次底层的叶子节点无空隙地紧密排列在这一层右侧；

d、次底层节点的度为 1 时，该节点没有右子节点。

在同样节点数的二叉树中，不存在其他形态的二叉树深度小于完全二叉树。

2.2.3、满二叉树

满二叉树是一种特殊的完全二叉树，如图。

满二叉树的叶子节点只能出现在最下层，每个非叶子节点的分支节点度都为 2 。在所有同深度的二叉树中，满二叉树的节点最多。

2.3、二叉树规律

2.3.1、节点数规律

二叉树的叶子节点数量总是比度为 2 的节点数多 1 个。

根据上图可知，叶子节点数量增加总是伴随着度为 2 的节点数增加，而起初只有根节点时，叶子节点数为 1 ，度为 2 的节点数为 0 。因此无论如何增加节点，叶子节点数总是比度为 2 的节点数多 1 个。

2.3.2、完全二叉树标号规律

将完全二叉树节点如下图编号：

会发现完全二叉树左子节点编号是其 2 倍，右子节点编号是其 2 倍 +1 （重要性质，下一篇关于堆的内容会用到）。

2.3.3、完全二叉树深度

已知完全二叉树节点数为 n ，其深度为 $(int)log_{2}n+1$ 。

根据以下代码可以计算出完全二叉树的深度：

#include <math.h>
#include <stdio.h>int main()
{int nodeCount;scanf("%d", &nodeCount);int depth = (int)(log(nodeCount) / log(2)) + 1;printf("Depth = %d\n", depth);return 0;
}