文章目录
- Reinfocement Learning
- 六、随机近似与随机梯度下降(Stochastic Approximation & Stochastic Gradient Descent)
- 6.1 Robbins-Monro Algorithm
- 6.2 随机梯度下降
- 七、时序差分方法(Temporal-Difference Learning)
- 7.1 TD算法介绍
- 7.2 TD算法的收敛性
- 7.3 TD算法与MC算法的比较
- 7.4 Sarsa及其变种
- 7.5 Q-learning
- 7.6 on-policy learning & off-policy learning
- 7.7 summary
Reinfocement Learning
六、随机近似与随机梯度下降(Stochastic Approximation & Stochastic Gradient Descent)
6.1 Robbins-Monro Algorithm
Stochastic approximation (SA) 是指一大类求根和优化问题的随机迭代算法,与许多其他求根算法相比,SA 的强大之处在于它无需知道目标函数的表达式或其导数。Robbins-Monro算法是SA领域的开创工作。
假定我们想要此等式的根 w w w: g ( w ) = 0 g(w)=0 g(w)=0
当函数 g g g 的表达式已知或者它的导数已知的时候,求解当然很简单。但是当 g g g 未知的时候,问题就困难起来了。Robbins-Monro 算法是这样解决的:
w k + 1 = w k − a k g ∼ ( w k , η k ) w_{k+1}=w_k-a_k {\overset{\sim}{g}}(w_k,\eta_k) wk+1=wk−akg∼(wk,ηk)
其中 w k w_k wk 是对第 k k k 次根的估计, g ∼ ( w k , η k ) = g ( w k ) + η k {\overset{\sim}{g}}(w_k,\eta_k)=g(w_k)+\eta_k g∼(wk,ηk)=g(wk)+ηk 是第 k k k 个带有噪声(误差)的观测(输出), a k a_k ak 是正系数。
显然这个算法并不依赖于函数 g g g,但依赖于输入序列 w k w_k wk 和带有噪声输出序列 g ∼ ( w k , η k ) {\overset{\sim}{g}}(w_k,\eta_k) g∼(wk,ηk),框图如下:
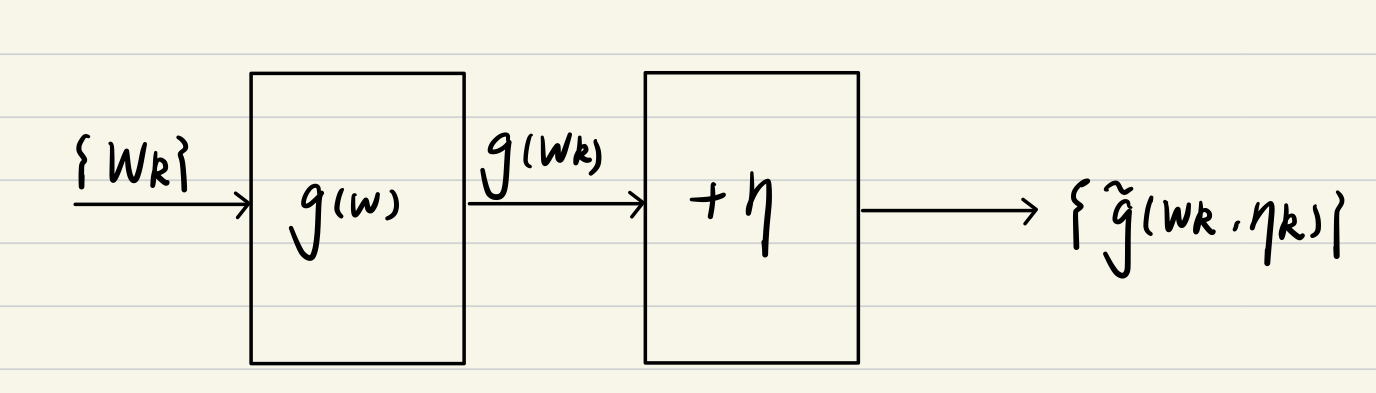
最终 w k + 1 w_{k+1} wk+1 能收敛到根 w ∗ w^* w∗。收敛性在此不做证明。
来看一个平均值求解的例子。如何求平均值,把所有数加起来除以个数当然能求得。但这样做的弊端是我必须要获取所有的数据后才能求其均值,如何使用迭代的方式求解呢?
我们可以假设 w k + 1 = 1 k ∑ k i = 1 x i w_{k+1}=\frac{1}{k}\underset{i=1}{\overset{k} \sum} x_i wk+1=k1i=1∑kxi,则 w k = 1 k − 1 ∑ k − 1 i = 1 x i w_{k}=\frac{1}{k-1}\underset{i=1}{\overset{k-1} \sum} x_i wk=k−11i=1∑k−1xi,所以 w k + 1 w_{k+1} wk+1 可以由 w k w_k wk 表示:
w k + 1 = 1 k ∑ k i = 1 x i = 1 k ( ∑ k − 1 i = 1 x i + x k ) = 1 k ( ( k − 1 ) w k + x k ) = w k − 1 k ( w k − x k ) w_{k+1}=\frac{1}{k}\underset{i=1}{\overset{k} \sum} x_i=\frac{1}{k}(\underset{i=1}{\overset{k-1} \sum}x_i+x_k)=\frac{1}{k}((k-1)w_k+x_k)=w_k-\frac{1}{k}(w_k-x_k) wk+1=k1i=1∑kxi=k1(i=1∑k−1xi+xk)=k1((k−1)wk+xk)=wk−k1(wk−xk)
就像这样:
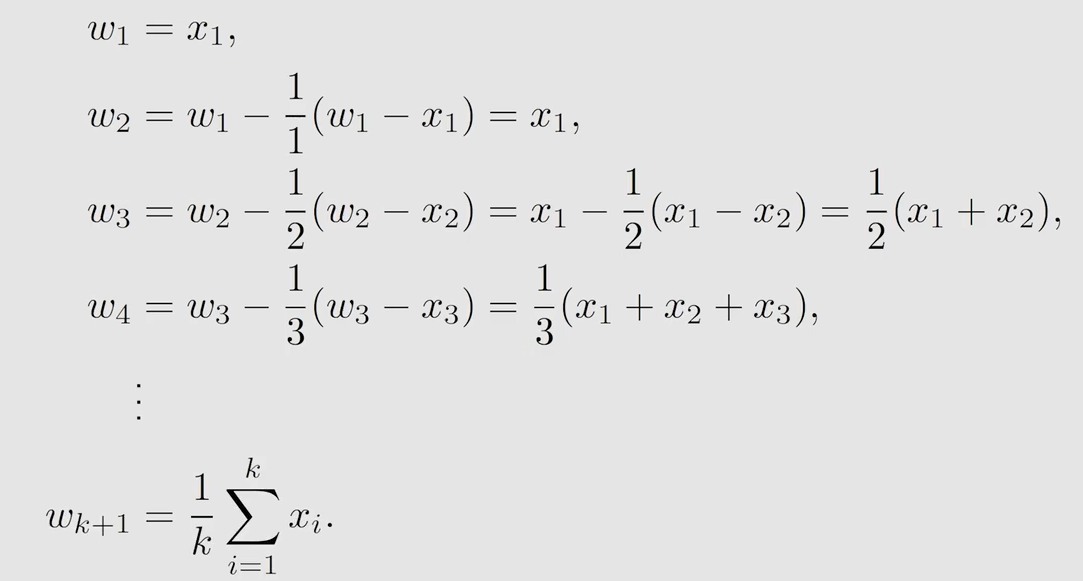
如果把 1 k \frac{1}{k} k1 变为 α k \alpha_k αk 还能成立吗?可以用上述的 Robbins-Monro Algorithm 来证明 w k + 1 w_{k+1} wk+1 仍然能收敛到期望。
问题转换为当 α k ≠ 1 k \alpha_k \neq \frac{1}{k} αk=k1 时, w k + 1 w_{k+1} wk+1 还能收敛到期望 E [ X ] \mathbb{E}[X] E[X] 吗?
我们有 w k + 1 = w k − α k ( w k − x k ) w_{k+1}=w_k-\alpha_k(w_k-x_k) wk+1=wk−αk(wk−xk)
建立如下函数 g ( w ) = w − E [ X ] g(w)=w-\mathbb{E}[X] g(w)=w−E[X],如果 g ( w ) = 0 g(w)=0 g(w)=0,根即为期望。
现输入一个 w w w,如何得到其噪音的观测呢?
g ∼ ( w , η ) = g ( w ) + η = ( w − E [ X ] ) + ( E [ X ] − x ) = w − x {\overset{\sim}{g}}(w,\eta)=g(w)+\eta=(w-\mathbb{E}[X])+(\mathbb{E}[X]-x)=w-x g∼(w,η)=g(w)+η=(w−E[X])+(E[X]−x)=w−x
现考虑 w k w_k wk 序列并带入到 Robbins-Monro 公式中得:
w k + 1 = w k − α k ( w k − x k ) w_{k+1}=w_k-\alpha_k(w_k-x_k) wk+1=wk−αk(wk−xk)
即得到证明:即使 α k ≠ 1 k \alpha_k \neq \frac{1}{k} αk=k1 时, w k + 1 w_{k+1} wk+1 仍能收敛到期望 E [ X ] \mathbb{E}[X] E[X] ?
6.2 随机梯度下降
Stochastic gradient descent(SGD)被广泛应用于机器学习和强化学习,但后面可以发现它实际上就是一种特殊的 Robbins-Monro 算法。
假设我们要求解一个最优化问题 w w w 何值时, J ( w ) J(w) J(w) 最小:
min w J ( w ) = E [ f ( w , X ) ] \underset{w}{\min}\quad J(w)=\mathbb{E}[f(w,X)] wminJ(w)=E[f(w,X)]
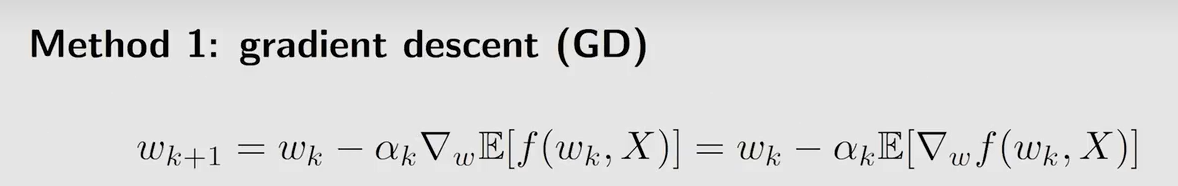
α k \alpha_k αk 是学习率(步长), ∇ \nabla ∇ 表示梯度,采用梯度下降的方法一定能找到一个局部极小值
期望很难求,用蒙特卡洛估计依靠数据近似期望
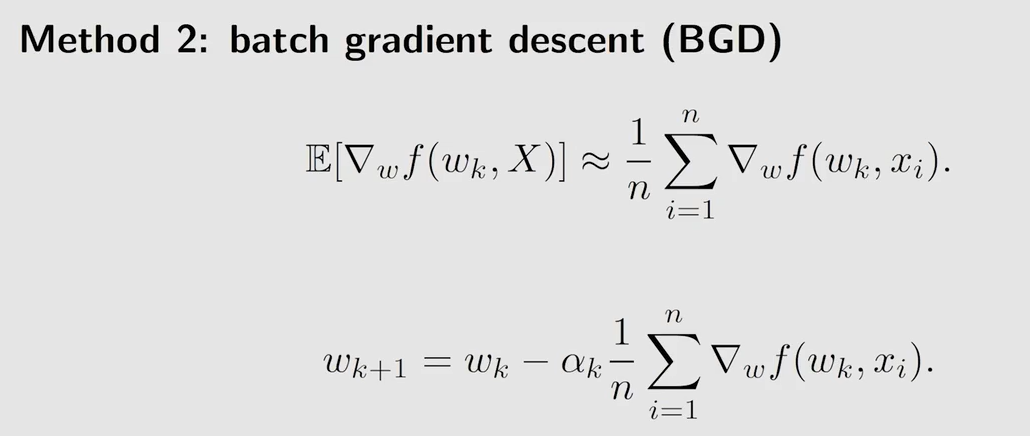
但每一次更新 w k w_k wk 时,都需要进行多次采样,现实中可能行不通
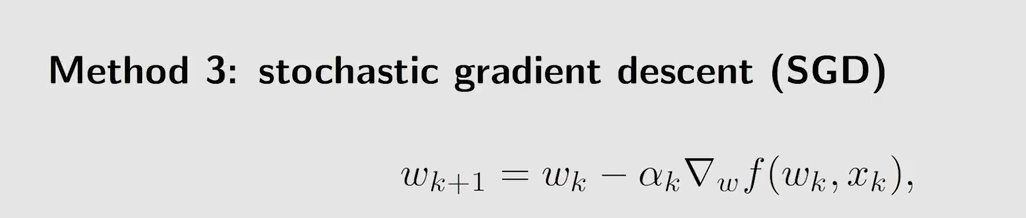
与 GD 相比使用随机梯度来代替真实的梯度,与 BGD 相比,使 n = 1 n=1 n=1,即采样一次。
例子:
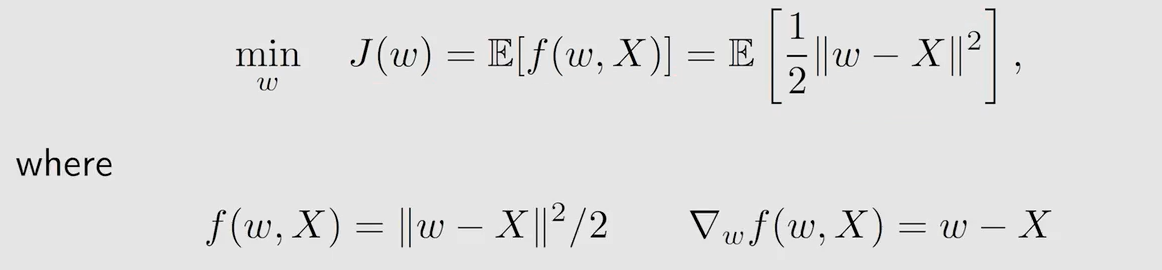

为什么 SGD 是可以收敛的呢?同样时使用 Robbins-Monro 证明。
现在有目标函数 J ( w ) = E [ f ( w , X ) ] J(w)=\mathbb{E}[f(w,X)] J(w)=E[f(w,X)]
我想让它取得最小值,那么一个必要条件时取得最小值时的梯度为0,即 ∇ w J ( w ) = E [ ∇ w f ( w , X ) ] = 0 \nabla_wJ(w)=\mathbb{E}[\nabla_w f(w,X)]=0 ∇wJ(w)=E[∇wf(w,X)]=0
令 g ( w ) = ∇ w J ( w ) = E [ ∇ w f ( w , X ) ] g(w)=\nabla_wJ(w)=\mathbb{E}[\nabla_w f(w,X)] g(w)=∇wJ(w)=E[∇wf(w,X)],此时变成了 g ( w ) = 0 g(w)=0 g(w)=0 的求根问题
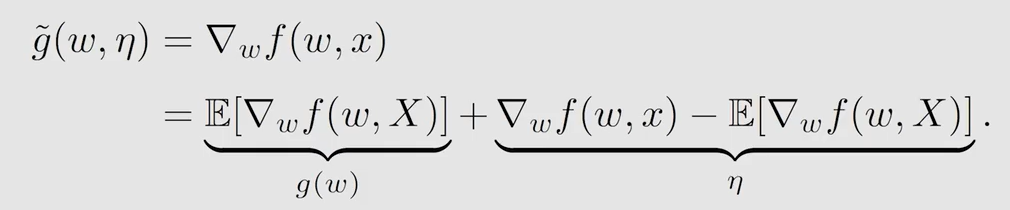
故
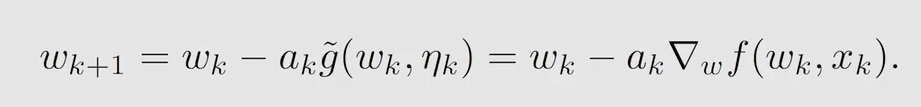
七、时序差分方法(Temporal-Difference Learning)
7.1 TD算法介绍
TD 算法是 m o d e l − f r e e model-free model−free 的算法
由给定的策略 π \pi π 在 t t t 时刻可以得到序列 { ( s t , r t + 1 , s t + 1 ) } t \{(s_t,r_{t+1},s_{t+1})\}_t {(st,rt+1,st+1)}t, s t s_t st 表示 t t t 时刻所在的状态
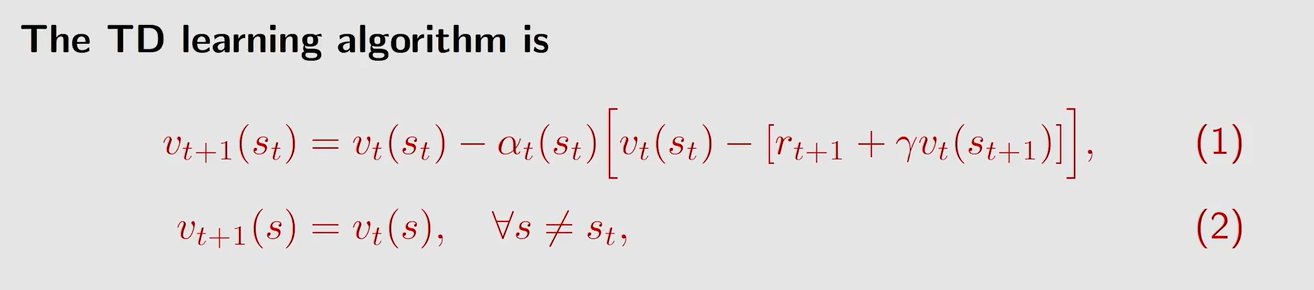
式中 v t v_t vt 代表在 t t t 时刻状态 s s s 的 s t a t e v a l u e state \ value state value (即 v π v_{\pi} vπ)的估计值,这个式子就是要用 v t v_t vt 来不断逼近 s t a t e v a l u e state \ value state value
( 1 ) (1) (1) 式表示更新当前状态 s t s_t st 的 s t a t e v a l u e state \ value state value 估计值 v t + 1 ( s t ) v_{t+1}(s_t) vt+1(st)
( 2 ) (2) (2) 式表示其余状态的的 s t a t e v a l u e state \ value state value 估计值不进行更新
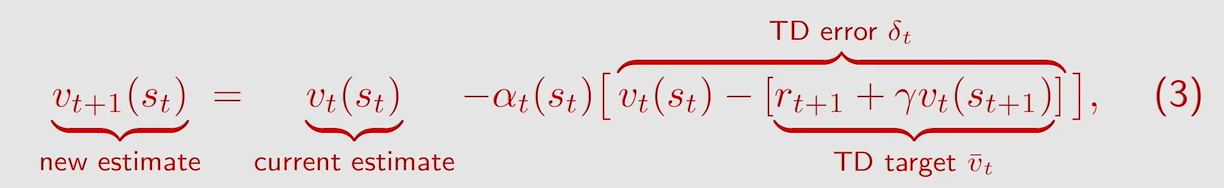
q u e s t i o n 1 question1 question1:为什么 v − t \overset{-}v_t v−t 被称作 T D t a r g e t TD \ target TD target?
a n s w e r 1 answer1 answer1:因为此算法是要把 v t ( s t ) v_t(s_t) vt(st) 朝着 v − t \overset{-}v_t v−t 的方向改进
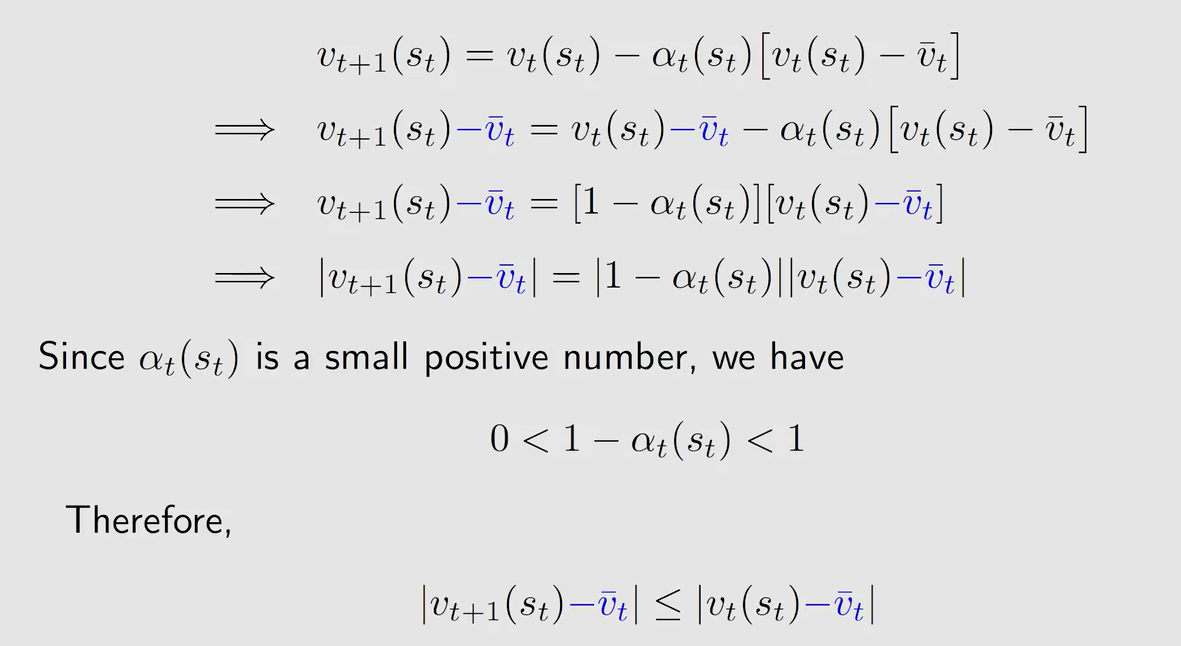
q u e s t i o n 2 question2 question2: T D e r r o r TD \ error TD error 是什么?
a n s w e r 2 answer2 answer2:
- 两个时刻的差值
- 描述了 v t v_t vt 与 v π v_{\pi} vπ 之间的误差
T D A l g o r i t h m p r o p e r t i e s TD \ Algorithm \ properties TD Algorithm properties:
- 对给定的策略进行 p o l i c y e v a l u a t i o n policy \ evaluation policy evaluation ,即计算 s t a t e v a l u e state \ value state value(不能估计 a c t i o n v a l u e action \ value action value,不能寻找最优策略)
- 核心思想就是对于给定的策略,我对状态 s s s 的 v π v_{\pi} vπ 有一个估计,这可能是不准确的,此时将得到的 { ( s t , r t + 1 , s t + 1 ) } t \{(s_t,r_{t+1},s_{t+1})\}_t {(st,rt+1,st+1)}t 与估计联系到一起,得到 T D e r r o r TD \ error TD error,这说明了此时的估计是不准确的,并利用 T D e r r o r TD \ error TD error 来改进当前的估计。
7.2 TD算法的收敛性
TD 算法其实是求解了这样一个贝尔曼公式:
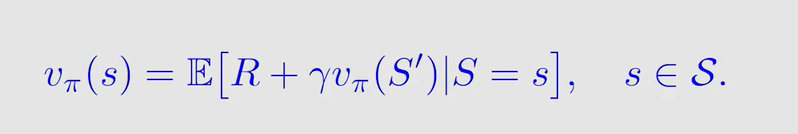
就是把原来的 G t + 1 G_{t+1} Gt+1 替换成了 v π ( S ′ ) v_{\pi}(S') vπ(S′) ,这是由 s t a t e v a l u e state \ value state value 最初始的定义得到的。
可以用 Robbins-Monro Algorithm 来求解这个公式,首先定义:
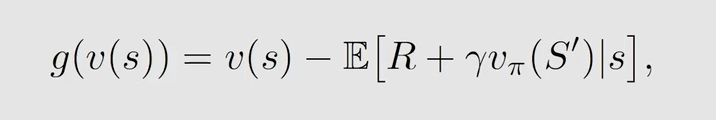
如果 g ( v ( s ) ) = 0 g(v(s))=0 g(v(s))=0,那么 v ( s ) = E [ R + γ v π ( S ′ ∣ s ) ] v(s)=\mathbb{E}[R+\gamma v_{\pi}(S'|s)] v(s)=E[R+γvπ(S′∣s)] 成立,就可以用 v ( s ) v(s) v(s) 来逼近 v π ( s ) v_{\pi}(s) vπ(s)。我们有大量 R , S ′ R,S' R,S′ 的数据采样 r , s ′ r,s' r,s′
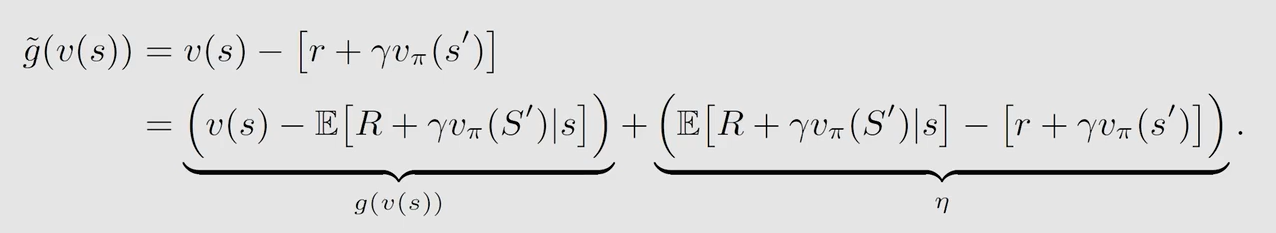
得到:
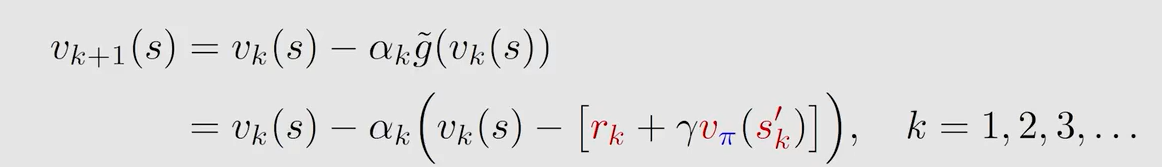
此式存在两个问题。
q u e s t i o n 1 question1 question1:式子是由 { ( s , r , s ′ ) } \{(s,r,s')\} {(s,r,s′)} 的得到的,如何确保它是按序的呢?
a n s w e r 1 answer1 answer1:将 { ( s , r , s ′ ) } \{(s,r,s')\} {(s,r,s′)} 替换为一个 t r a j e c t o r y trajectory trajectory 中的 { ( s t , r t + 1 , s t + 1 ) } \{(s_t,r_{t+1},s_{t+1})\} {(st,rt+1,st+1)}
q u e s t i o n 2 question2 question2:式中的 v π ( s k ′ ) v_{\pi}(s_k') vπ(sk′) 是不知道的
a n s w e r 2 answer2 answer2:用 v k ( s k ′ ) v_{k}(s_k') vk(sk′) 即 v π ( s k ′ ) v_{\pi}(s_k') vπ(sk′) 的估计值来代替 v π ( s k ′ ) v_{\pi}(s_k') vπ(sk′) ,仍能使得 v k ( s ) v_k(s) vk(s) 收敛
7.3 TD算法与MC算法的比较
| TD Learning | MC Learning |
|---|---|
| O n l i n e Online Online:能够在收到一个 r e w a r d reward reward 后立即更新 s t a t e / a c t i o n v a l u e state/action \ value state/action value | O f f l i n e Offline Offline:必须要等到一个 e p i s o d e episode episode 结束才能计算 r e t u r n return return |
| C o n t i n u i n g t a s k s Continuing \ tasks Continuing tasks:可以处理连续的任务( e p i s o d e episode episode 无限长) | E p i s o d i c t a s k s Episodic \ tasks Episodic tasks:只能处理一个 e p i s o d e episode episode 有 t e r m i n a l s t a t e terminal \ state terminal state 的任务 |
| B o o t s t r a p p i n g Bootstrapping Bootstrapping:更新 v a l u e value value 依赖于先前 v a l u e value value 的估计值 | N o n − b o o t s t r a p p i n g Non-bootstrapping Non−bootstrapping:可以直接估计 s t a t e / a c t i o n v a l u e state/action \ value state/action value |
| L o w e s t i m a t i o n v a r i a n c e Low \ estimation \ variance Low estimation variance:相较于 MC 有较少的随机变量,但是是有偏估计(由初始的估计造成) | H i g h e s t i m a t i o n v a r i a n c e High \ estimation \ variance High estimation variance:为估计 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a) 涉及到的随机变量较多,采样数量少的情况下方差较大,是无偏估计 |
7.4 Sarsa及其变种
S a r s a Sarsa Sarsa 可以给出给定策略 π \pi π 的 a c t i o n v a l u e action \ value action value
假设有集合 { ( s t , a t , r t + 1 , s t + 1 , a t + 1 ) } t \{(s_t,a_t,r_{t+1},s_{t+1},a_{t+1})\}_t {(st,at,rt+1,st+1,at+1)}t
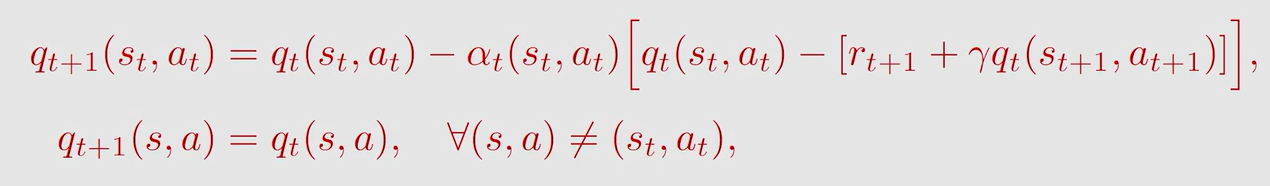
形式上跟 T D TD TD 算法是一样的,只是 T D TD TD 得到的是 s t a t e v a l u e state \ value state value 的估计值,而 S a r s a Sarsa Sarsa 是 a c i t o n v a l u e aciton \ value aciton value 的估计值
S a r s a Sarsa Sarsa 求解的是这样的贝尔曼公式:
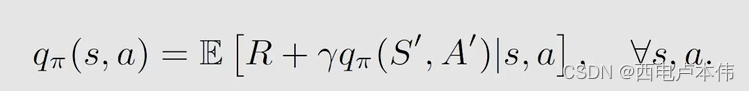
在求得 a c t i o n v a l u e action \ value action value 之后,使用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy 的策略进行 p o l i c y i m p r o v e m e n t policy \ improvement policy improvement。
算法存在的问题是:如果 e p i s o d e episode episode 不足以覆盖全部的 ( s , a ) (s,a) (s,a),那么可能找不到全局的最优策略。
E x p e c t e d S a r s a Expected \ Sarsa Expected Sarsa
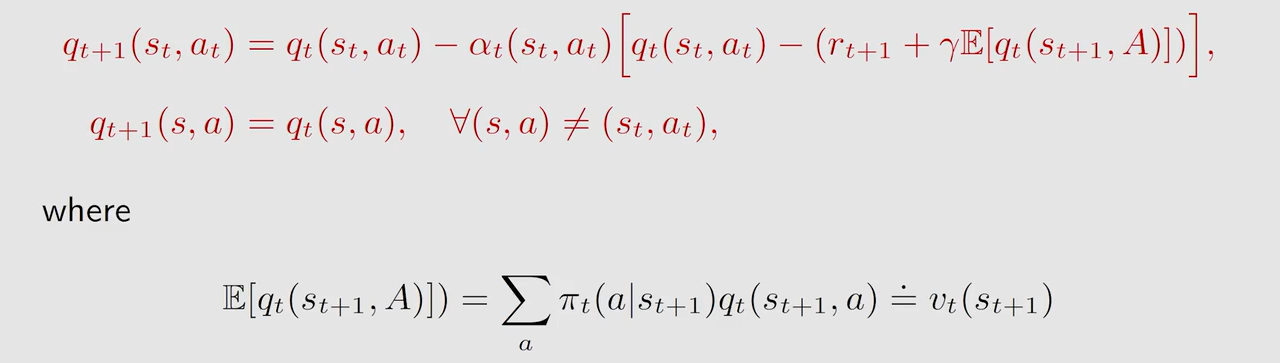
不需要再对 a t + 1 a_{t+1} at+1 进行采样, E x p e c t e d S a r s a Expected \ Sarsa Expected Sarsa 求解的是这样的贝尔曼公式:
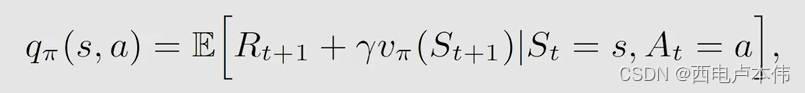
n − s t e p S a r s a n-step\ Sarsa n−step Sarsa 需要的集合为 { ( s t , a t , r t + 1 , s t + 1 , a t + 1 ) , . . . , r t + n , s t + n , a t + n } t \{(s_t,a_t,r_{t+1},s_{t+1},a_{t+1}),...,r_{t+n},s_{t+n},a_{t+n}\}_t {(st,at,rt+1,st+1,at+1),...,rt+n,st+n,at+n}t,而 M C MC MC 是需要整个的 e p i s o d e episode episode,即所有的 s t a t e − a c t i o n p a i r state-action \ pair state−action pair
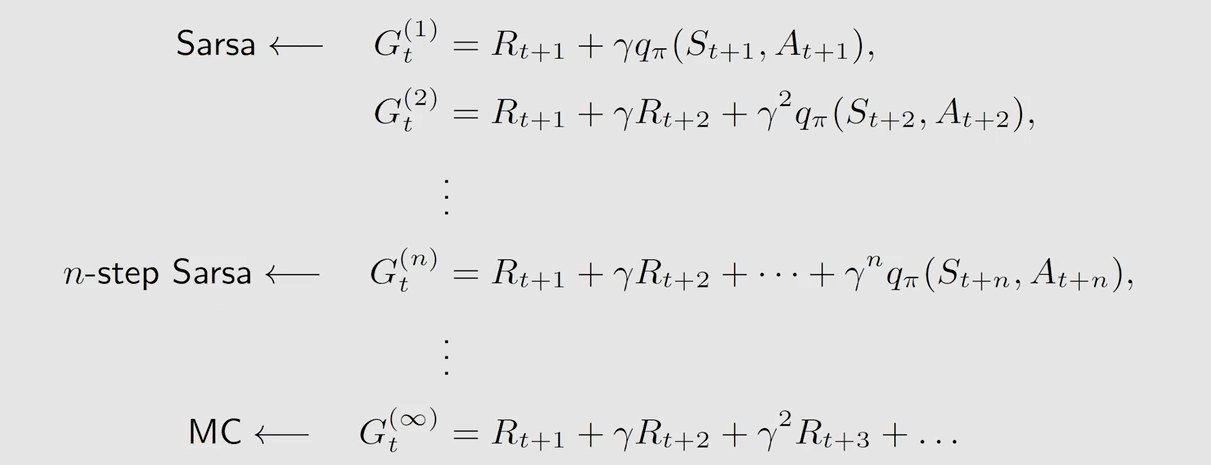
区别在于后面的 T D t a r g e t TD \ target TD target 不同
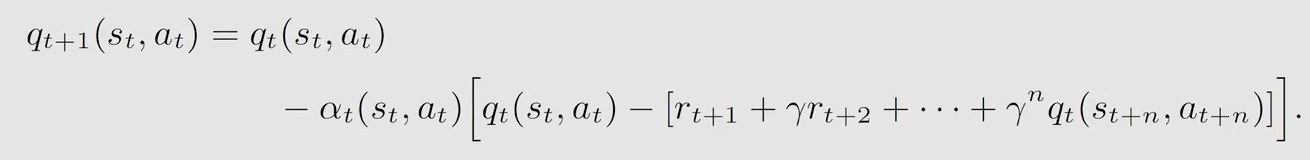
7.5 Q-learning
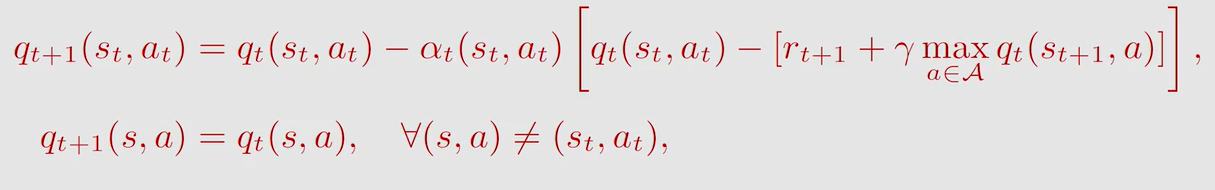
跟 S a r s a Sarsa Sarsa 相比也是 T D t a r g e t TD \ target TD target 不同, Q − l e a r n i n g Q-learning Q−learning 取的是让状态 s t + 1 s_{t+1} st+1 的 a c t i o n v a l u e action \ value action value 取得最大值时的动作 a a a,而 S a r s a Sarsa Sarsa 是随机采样一个 a a a
Q − l e a r n i n g Q-learning Q−learning 求解的是贝尔曼最优方程:
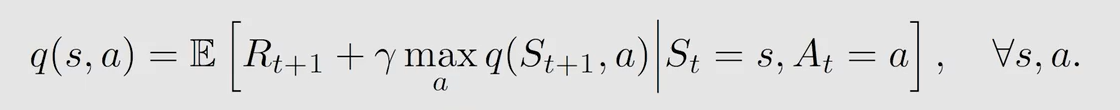
得到的值是最优的 a c t i o n v a l u e action \ value action value,当然对应的是最优策略
7.6 on-policy learning & off-policy learning
在 T D L e a r n i n g TD \ Learning TD Learning 中有两种策略:
- b e h a v i o r p o l i c y behavior \ policy behavior policy:用于生成 e x p e r i e n c e s a m p l e s experience \ samples experience samples(即前面所说的 { ( s t , a t , r t + 1 , s t + 1 , a t + 1 ) } t \{(s_t,a_t,r_{t+1},s_{t+1},a_{t+1})\}_t {(st,at,rt+1,st+1,at+1)}t 这样的序列)
- t a r g e t p o l i c y target \ policy target policy:持续向最优策略更新
由此引出 o n − p o l i c y on-policy on−policy 与 o f f − p o l i c y off-policy off−policy:
- o n − p o l i c y on-policy on−policy: b e h a v i o r p o l i c y behavior \ policy behavior policy 与 t a r g e t p o l i c y target \ policy target policy 相同,即用一个策略 π \pi π 与环境交互得到 e x p e r i e n c e experience experience 同时改进这个策略 π \pi π ,再用改进的策略 π ′ \pi' π′ 与环境交互然后再改进直到得到最优策略 π ∗ \pi^* π∗
- o f f − p o l i c y off-policy off−policy: b e h a v i o r p o l i c y behavior \ policy behavior policy 与 t a r g e t p o l i c y target \ policy target policy 不相同,即用一个策略 π \pi π 与环境交互得到 e x p e r i e n c e experience experience 同时改进另外一个策略 π ′ \pi' π′ ,再用策略 π \pi π 与环境交互然后再改进 π ′ \pi' π′ 直到得到最优策略 π ∗ \pi^* π∗
S a r s a Sarsa Sarsa 是 o n − p o l i c y on-policy on−policy: π t → e x p e r i e n c e → a c t i o n v a l u e e s t i m a t i o n → π t + 1 \pi_t \rightarrow experience \rightarrow action \ value \ estimation \rightarrow \pi_{t+1} πt→experience→action value estimation→πt+1, π t \pi_t πt 既是 b e h a v i o r p o l i c y behavior \ policy behavior policy 也是 t a r g e t p o l i c y target \ policy target policy
M o n t e − C a r l o Monte-Carlo Monte−Carlo 是 o n − p o l i c y on-policy on−policy: π t → e x p e r i e n c e / t r a j e c t o r y → a c t i o n v a l u e e s t i m a t i o n → π t + 1 \pi_t \rightarrow experience / trajectory \rightarrow action \ value \ estimation \rightarrow \pi_{t+1} πt→experience/trajectory→action value estimation→πt+1, π t \pi_t πt 既是 b e h a v i o r p o l i c y behavior \ policy behavior policy 也是 t a r g e t p o l i c y target \ policy target policy
Q − l e a r n i n g Q-learning Q−learning 是 o f f − p o l i c y off-policy off−policy: 由 s t s_t st 选择动作 a t a_t at 的 b e h a v i o r p o l i c y behavior \ policy behavior policy 可以是任意策略, t a r g e t p o l i c y target\ policy target policy 是根据最大 a c t i o n v a l u e action \ value action value 确定的最优策略
Q − l e a r n i n g Q-learning Q−learning 可以是 o n − p o l i c y on-policy on−policy 的,也可以是 o f f − p o l i c y off-policy off−policy 的

用更新的 π t + 1 \pi_{t+1} πt+1 继续生成 e x p e r i e n c e experience experience,在 p o l i c y i m p r o v e m e n t policy \ improvement policy improvement 阶段采用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy 是希望策略具有一定的探索性,希望能覆盖到所有的 ( s , a ) (s,a) (s,a)

用 π b \pi_b πb (此策略生成的 e p i s o d e episode episode 会对 Q − l e a r n i n g Q-learning Q−learning 的结果产生影响)来生成 e x p e r i e n c e experience experience,在 p o l i c y i m p r o v e m e n t policy \ improvement policy improvement 阶段采用 g r e e d y greedy greedy 是因为我不会用改进的策略来生成 e x p e r i e n c e experience experience,所以选最优的即可
7.7 summary
前面介绍的 T D TD TD 算法其实都可以用下面的式子统一表示:
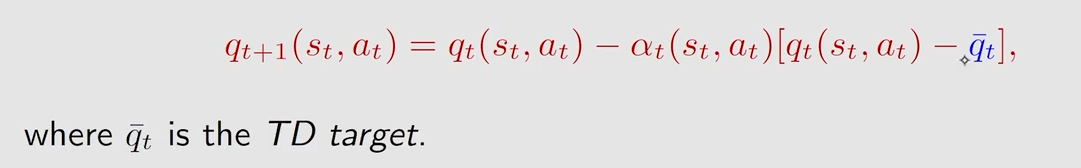
不同点在于 q t − \overset{-}{q_t} qt−:

所有的算法也可以看作是求解贝尔曼公式或者贝尔曼最优公式的随即近似算法:








)

:前缀和)




)




