引言：“生活中的模糊关系”

如果说，我们简单的将 温度<10度 的天气称为冷， 10度>温度> 25度 的天气称为温暖，将 温度>25度的天气称为热，这种模糊性就消除了，这在数学上没有任何问题，然而就这1度之差，就将“冷”变为“温暖”，“温暖”变为“热”，这又不符合我们日常的生活习惯
在企图用数学处理生活中的问题时，精确的数学语言和模糊的思维习惯产生了矛盾。 模糊逻辑就是用来解决这一矛盾的工具之一

模糊集合

模糊集合（fuzzy set）是对经典集合的扩充。下面先介绍集合论中的几个名词。

1. 论域：要讨论的全体对象，常用U、E等大写字母表示。
2. 元素：论域中的每个对象，常用a，b，c，x，y，z等小写字母表示。
3. 集合：论域中具有某种相同属性的确定的，可以彼此区别的元素的全体，常用A，B，C，X，Y，Z等表示，例如 A = { x ∣ f ( x ) > 0 } A=\{x|f(x)>0\} A={x∣f(x)>0}

模糊集合的定义

 设存在一个普通论域$U$，$U$到$[0,1]$区间的任一映射$f$都可以确定$U$的一个模糊集合，称为$U$上的模糊集合$A$。其中映射$f$叫做模糊集的隶属度函数，对于$U$上一个元素$u$，$f(u)$叫做$u$对于模糊集的隶属度，也可写作$A(u)$

模糊集合的表示法

模糊集合 : A ( u ) = { u ∣ f ( u ) } 模糊集合:A (u)= \{ u|f(u)\} 模糊集合:A(u)={u∣f(u)}

1. Zadeh表示法

   • 当论域为离散集合时，一个模糊集合可以表示为：
     $$A=\sum _{u\in U}\frac{f_A(u)}{u}$$
   • 当论域为连续集合时，一个模糊集合可以表示为：$$A=\underset{u}{\int }\frac{f_A(u)}{u}$$

   注意：这里仅仅是借用了求和与积分的符号，并不表示求和与积分，仅仅代表集合

2. 序数表示法

   • 对于一个模糊集合来说，如果给出了论域上所有的元素以及其对应的隶属度，就等于表示出了该集合。所以，序对表示法出现了。$$A=\{(u,f_a(u))|u\in U\}$$

$U$：论域、$u_A(u)$：隶属函数、$u$：元素

模糊集合表示法示例

如果加上，这篇文章篇幅过长了，劳烦看客移步：模糊集合表示法示例

隶属函数

本节多有借鉴：隶属函数的确定–Evanism_小风铃

$$隶属度函数：A_u(u)$$
 ：若对论域（研究的范围）U中的任一元素x，都有一个数A(x)∈[0，1]与之对应，则称A为U上的模糊集，A(x)称为x对A的隶属度。当x在U中变动时，A(x)就是一个函数，称为A的隶属函数。

常见的隶属度函数：

确定隶属函数常用的方法有以下三种：

• 模糊统计法
• 指派法
• 借用已有的客观尺度

---

模糊统计法

---

指派法
指派法通过已有的函数模型，将自己的实例放入对应的函数模型中完成隶属函数的确定。

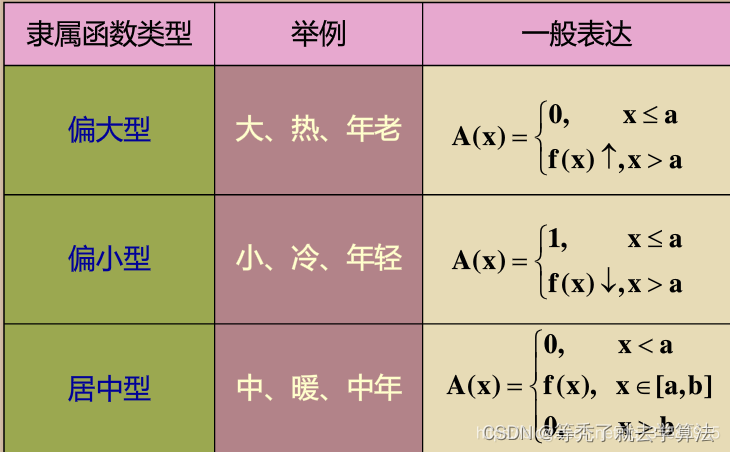
• 偏大型的f(x)常常为增函数，而偏小型的为减函数

---

借用已有的客观尺度

以上隶属函数选用,可以参照指派法

---

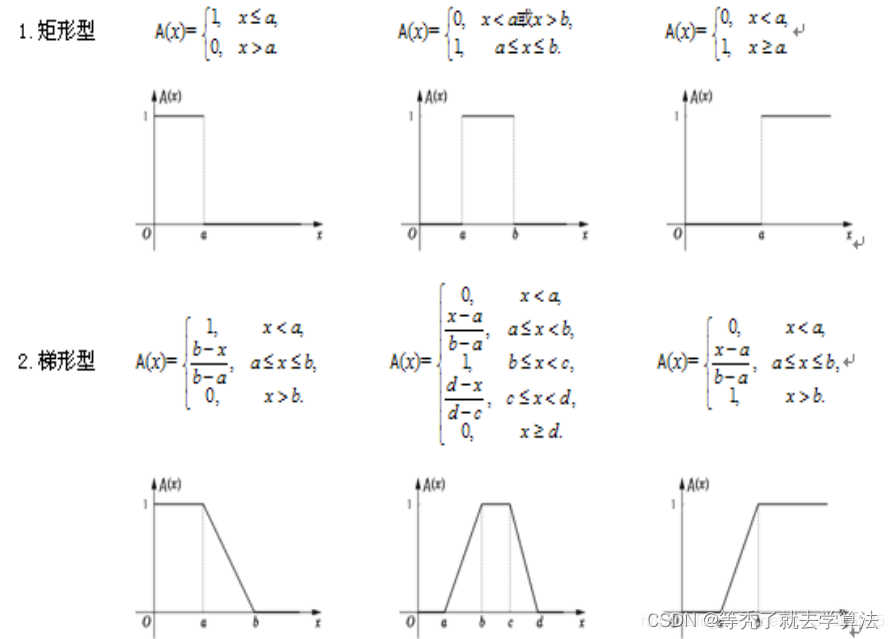
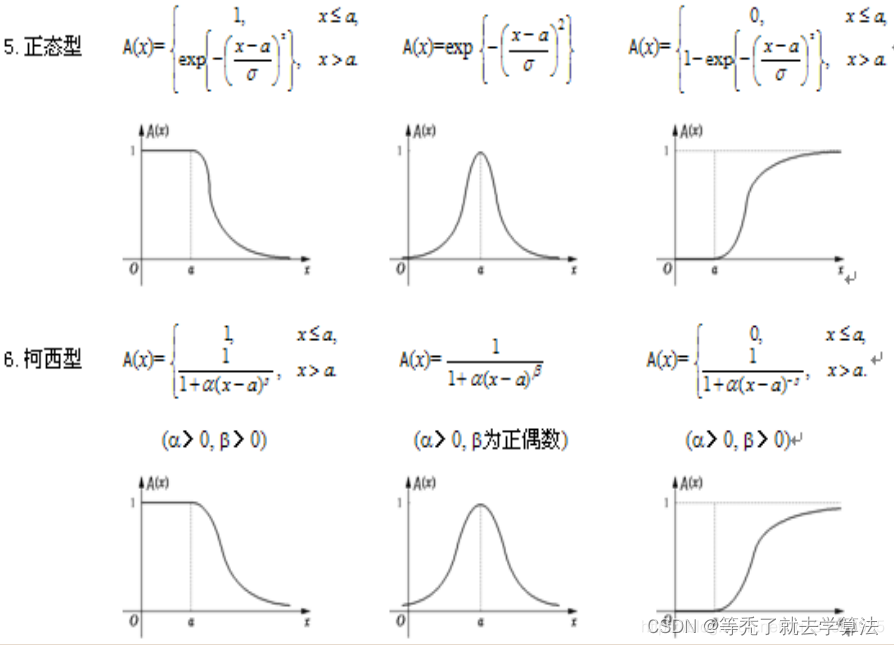
为了不让此篇博客篇幅过长，以上所有出现的隶属函数的JAVA实现和具体的使用方法，劳烦移步：【人工智能】模糊隶属函数

模糊规则

回到最初的问题：
step1：找出语言变量（冷，温暖，热，多，少，随性）的所对应区间（模糊集合）、论域（取值范围）

• （模糊规则）： 如果天气冷，所以多穿衣服。
• （变量$u_A$取值范围）：温度[-∞,+∞] ,但可以做出<10,[10,25],>25三个区间
• （变量$u_B$取值范围）：穿衣指数[1，10]，可以做出,[1,3],[3,6],[6,10]三个区间

这里穿衣指数仅仅是为了解题而假设出来，并没有实际含义
温度：<10：冷的区间； [10,25]:温暖的区间；>25：热的区间
穿衣指数：[1,3]:少的区间；[3,6]：随性区间；[6,10]：多的区间

step2：依据经验，使用合适的模糊隶属函数将模糊集合表示出来

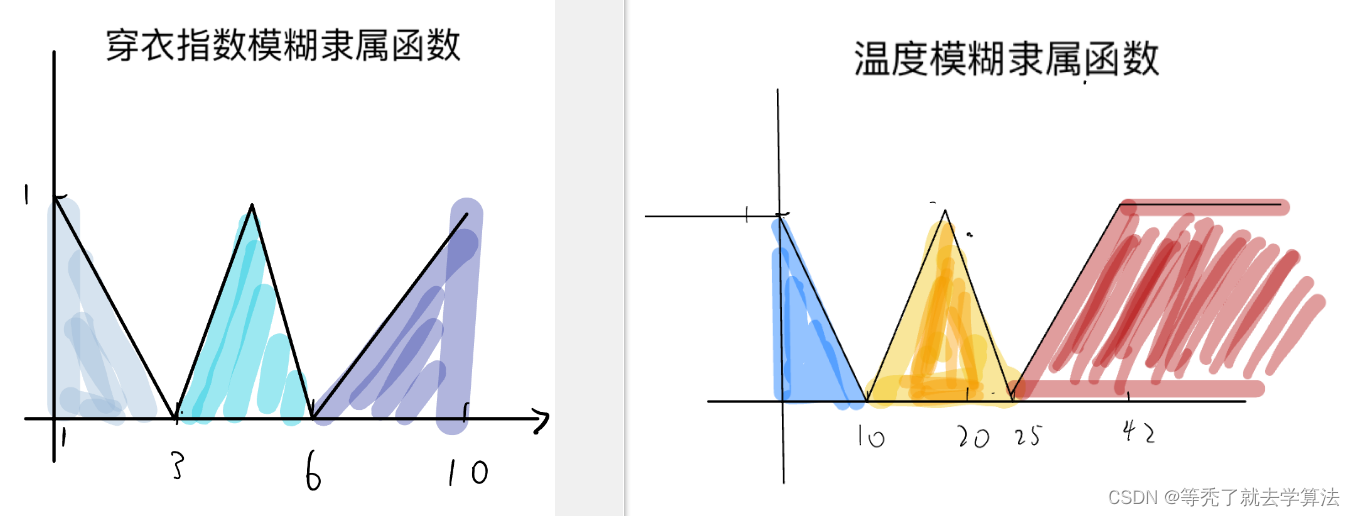
我所采用的是三角模糊隶属函数、和梯型模糊隶属函数，将其表示出来
可以得到，各自的隶属函数

这样，就可以得到任意一个温度，或者穿衣指数对其模糊集合的隶属度，

例如，$A(23)${冷“”–0，“温暖”–0.267，“热”–0} $B(4)${“少”–0 ，“随性”–0.67，“多”–0}

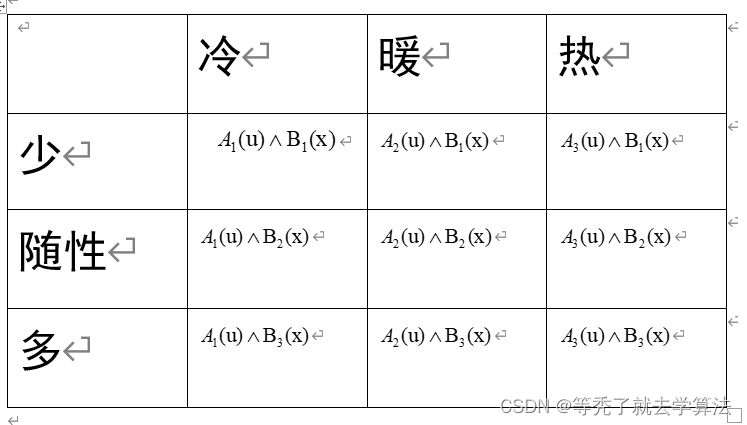
step3：将所得到的隶属函数，组合成模糊关系矩阵

那么我们将规则做一个矩阵化处理，得到模糊关系：

例如，$A(23)${冷“”–0，“温暖”–0.267，“热”–0} $B(4)${“少”–0 ，“随性”–0.67，“多”–0}
$A(23)\to B(4)$ ={0 0 0;0 0.267 0;0 0 0} ，
也就是说
大前提：如果温暖，则舒适随性
小前提：23，则4，
结论：置信度是0.267

模糊计算的流程

模糊计算的过程可以分为四个模块：
模糊规则库、模糊化、推理方法和去模糊化

模糊规则库是专家提供的模糊规则。模糊化是根据隶属度函数从具体的输入得到对模糊集隶属度的过程。推理方法是从模糊规则和输入对相关模糊集的隶属度得到模糊结论的方法。去模糊化就是将模糊结论转化为具体的、精确的输出的过程。

示例：如果加上篇幅过长，劳烦移步：模糊推理附录（2）