1.了解数据结构和算法

1.1 二分查找

        二分查找（Binary Search）是一种在有序数组中查找特定元素的搜索算法。它的基本思想是将数组分成两半，然后比较目标值与中间元素的大小关系，从而确定应该在左半部分还是右半部分继续查找。这个过程不断重复，直到找到目标值或确定它不存在于数组中。

1.1.1 二分查找的实现

（1）循环条件使用 "i <= j" 而不是 "i < j" 是因为，在二分查找的过程中，我们需要同时更新 i 和 j 的值。当 i 和 j 相等时，说明当前搜索范围只剩下一个元素，我们需要检查这个元素是否是我们要找的目标值。如果这个元素不是我们要找的目标值，那么我们可以确定目标值不存在于数组中。

如果我们将循环条件设置为 "i < j"，那么当 i 和 j 相等时，我们就无法进入循环来检查这个唯一的元素，这会导致我们无法准确地判断目标值是否存在。

因此，在二分查找的循环条件中，我们应该使用 "i <= j"，以确保我们在搜索范围内包含所有可能的元素。

（2）如果你使用 "i + j / 2" 来计算二分查找的中间值，可能会遇到整数溢出的问题。这是因为在 Java 中，整数除法（/）对整数操作时会向下取整，结果仍然是一个整数。例如，如果 i 和 j 都是很大的数，且它们相加结果大于 Integer.MAX_VALUE（即 2^31 - 1），那么直接将它们相加再除以 2 就会导致溢出，因为中间结果已经超出了 int 类型的最大值（会变成负数）。

public static void main(String[] args) {int[]arr={1,22,33,55,88,99,117,366,445,999};System.out.println(binarySearch( arr,1));//结果：0System.out.println(binarySearch( arr,22));//结果：1System.out.println(binarySearch( arr,33));//结果：2System.out.println(binarySearch( arr,55));//结果：3System.out.println(binarySearch( arr,88));//结果：4System.out.println(binarySearch( arr,99));//结果：5System.out.println(binarySearch( arr,117));//结果：6System.out.println(binarySearch( arr,366));//结果：7System.out.println(binarySearch( arr,445));//结果：8System.out.println(binarySearch( arr,999));//结果：9System.out.println(binarySearch( arr,1111));//结果：-1System.out.println(binarySearch( arr,-1));//结果：-1}/*** @Description* @Author LY* @Param [arr, target] 待查找升序数组，查找的值* @return int 找到返回索引，找不到返回-1* @Date 2023/12/8 16:38**/public static int binarySearch(int[] arr, int target){//设置 i跟j 初始值int i=0;int j= arr.length-1;//如果i>j，则表示并未找到该值while (i<=j){int m=(i+j)>>>1;
//            int m=(i+j)/2;if (target<arr[m]){//目标在左侧j=m-1;}else if(target>arr[m]){//目标在右侧i=m+1;}else{//相等return m;}}return -1;}

 1.1.2 二分查找改动版

        方法 binarySearchAdvanced 是一个优化版本的二分查找算法。它将数组范围从 0 到 arr.length 进行划分（改动1），并且在循环条件中使用 i < j 而不是 i <= j （改动2）。这种修改使得当目标值不存在于数组中时，可以更快地结束搜索。此外，在向左移动右边界时，只需将其设置为中间索引 m 而不是 m - 1 （改动3）。

        这些改动使 binarySearchAdvanced 在某些情况下可能比标准二分查找更快。然而，在实际应用中，这些差异通常很小，因为二分查找本身的复杂度已经很低（O(log n)）。

/*** @return int 找到返回索引，找不到返回-1* @Description 二分查找改动版* @Author LY* @Param [arr, target] 待查找升序数组，查找的值* @Date 2023/12/8 16:38**/public static int binarySearchAdvanced(int[] arr, int target) {int i = 0;
//        int j= arr.length-1;int j = arr.length;//改动1
//        while (i<=j){while (i < j) {//改动2int m = (i + j) >>> 1;if (target < arr[m]) {
//                j = m - 1;j = m; //改动3} else if (arr[m] < target) {i = m + 1;} else {return m;}}return -1;}

 1.2 线性查找

        线性查找（Linear Search）是一种简单的搜索算法，用于在无序数组或列表中查找特定元素。它的基本思想是从数组的第一个元素开始，逐一比较每个元素与目标值的大小关系，直到找到目标值或遍历完整个数组。

（1）初始化一个变量 index 为 -1，表示尚未找到目标值。
（2）从数组的第一个元素开始，使用循环依次访问每个元素：
（3）如果当前元素等于目标值，则将 index 设置为当前索引，并结束循环。

（4）返回 index。（如果找到了目标值返回其索引；否则返回 -1 表示未找到目标值）

 /*** @return int 找到返回索引，找不到返回-1* @Description 线性查找* @Author LY* @Param [arr, target] 待查找数组（可以不是升序），查找的值* @Date 2023/12/8 16:38**/public static int LinearSearch(int[] arr, int target) {int index=-1;for (int i = 0; i < arr.length; i++) {if(arr[i]==target){index=i;break;}}return index;}

1.3 衡量算法第一因素

时间复杂度：算法在最坏情况下所需的基本操作次数与问题规模之间的关系。

1.3.1 对比

假设每行代码执行时间都为t，数据为n个，且是最差的执行情况（执行最多次）：

二分查找：

二分查找执行时间为：	5L+4： 既5*floor(log_2(x)+1)+4
执行语句	执行次数
int i=0;	1
int j=arr.length-1;	1
return -1;	1
循环次数为：floor(log_2(n))+1，之后使用L代替
i<=j;	L+1
int m= (i+j)>>>1;	L
artget<arr[m]	L
arr[m]<artget	L
i=m+1;	L

线性查找：

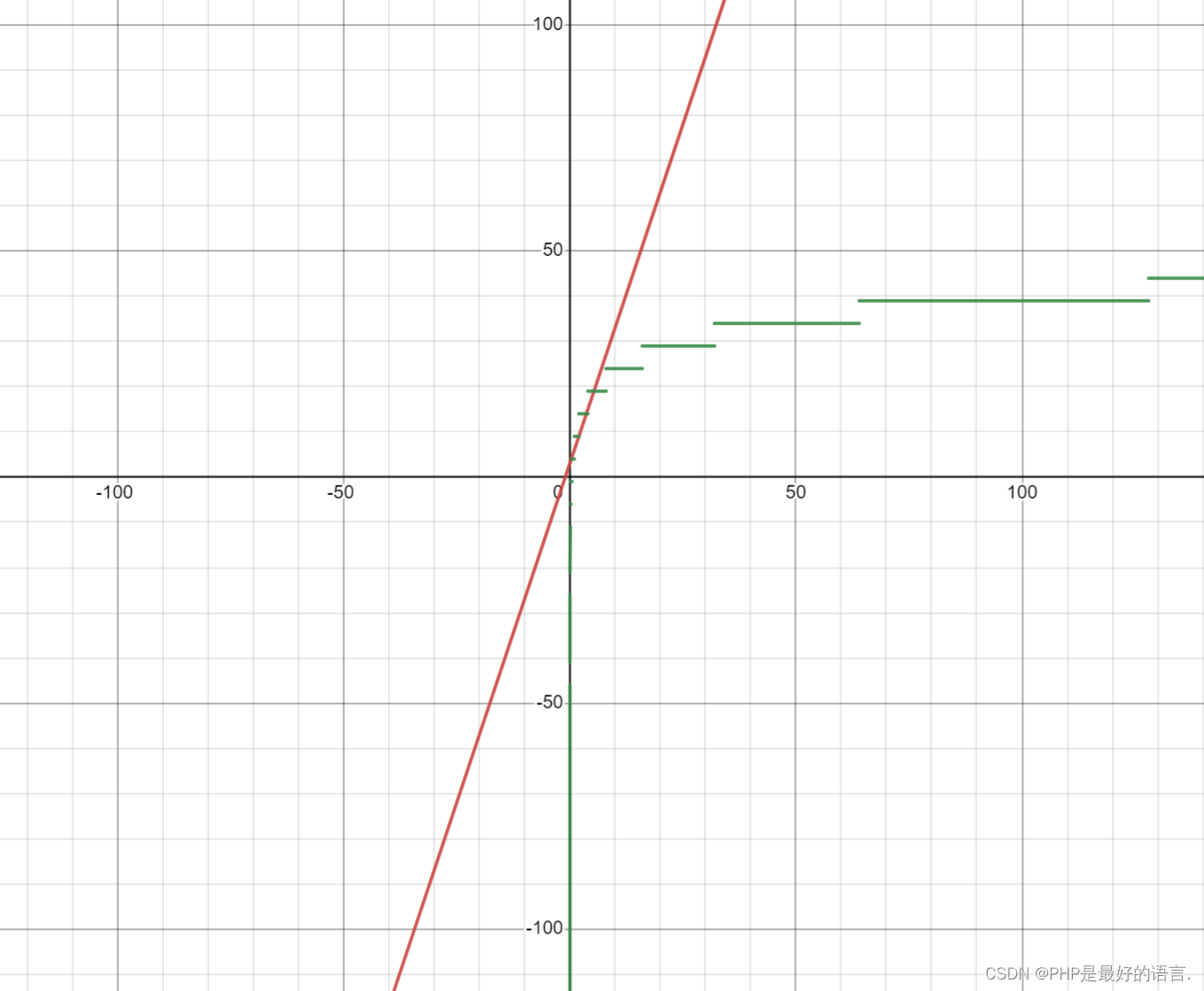
线性查找执行时间为：	3x+3
执行语句	执行次数
int i=0;	1
i<a.length;	x+1
i++;	x
arr[i]==target	x
return -1;	1

对比工具：Desmos | 图形计算器

对比结果：

随着数据规模增加，线性查找执行时间会逐渐超过二分查找。

1.3.2 时间复杂度

        计算机科学中，时间复杂度是用来衡量一个算法的执行，随着数据规模增大，而增长的时间成本（不依赖与环境因素）。

时间复杂度的标识：

        假设要出炉的数据规模是n，代码总执行行数用f(n)来表示：

                线性查找算法的函数：f(n)=3*n+3。

                二分查找算法函数：：f(n)=5*floor(log_2(x)+1)+4。

为了简化f(n)，应当抓住主要矛盾，找到一个变化趋势与之相近的表示法。

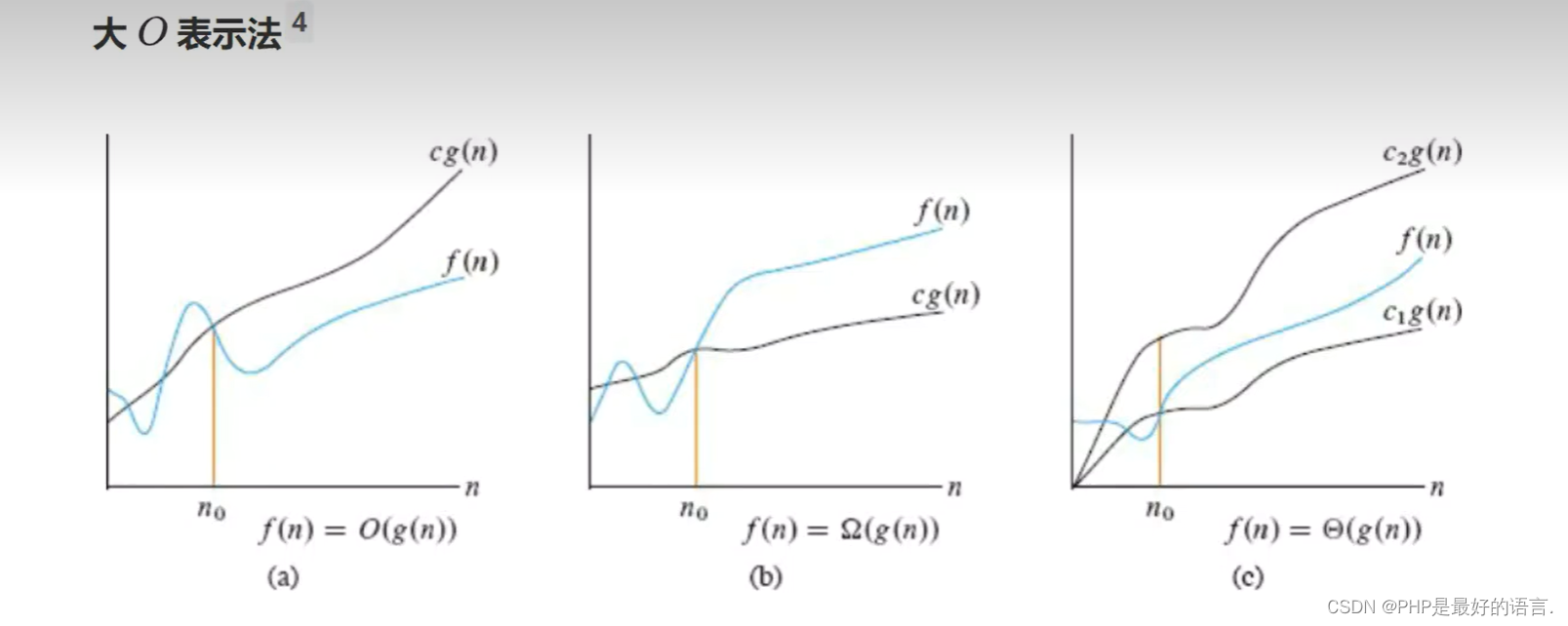
1.3.3 渐进上界

渐进上界代表算法执行的最差情况：

        以线性查找法为例：

                f(n)=3*n+3

                g(n)=n

        取c=4，在n0=3后，g(n)可以作为f(n)的渐进上界，因此大O表示法写作O(n)

        以二分查找为例：

                5*floor(log_2(n)+1)+4===》5*floor(log_2(n))+9

                g(n)=log_2(n)

                O(log_2(n))

1.3.4 常见大O表示法

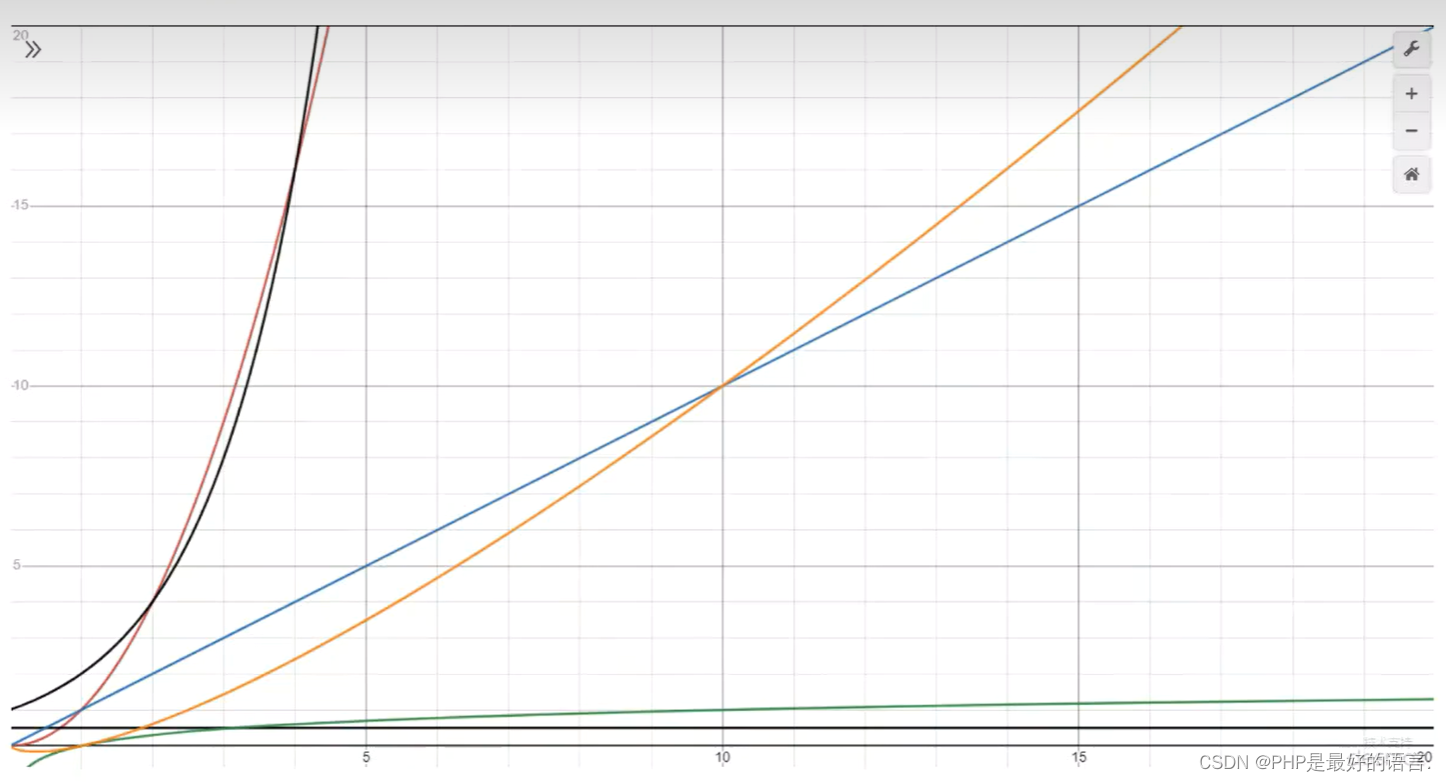
按时间复杂度，从低到高：

（1）黑色横线O(1)：常量时间复杂度，意味着算法时间并不随数据规模而变化。

（2）绿色O(log(n))：对数时间复杂度。

（3）蓝色O(n)：线性时间复杂度，算法时间与规模与数据规模成正比。

（4）橙色O(n*log(n))：拟线性时间复杂度。

（5）红色O(n^2)：平方时间复杂度。

（6）黑色向上O(2^n)：指数时间复杂度。

（7）O(n!)：这种时间复杂度非常大，通常意味着随着输入规模 n 的增加，算法所需的时间会呈指数级增长。因此，具有 O(n!) 时间复杂度的算法在实际应用中往往是不可行的，因为它们需要耗费大量的计算资源和时间。

1.4 衡量算法第二因素

空间复杂度：与时间复杂度类似，一般也用O衡量，一个算法随着数据规模增大，而增长的额外空间成本。

1.3.1 对比

以二分查找为例：

二分查找占用空间为：	4字节
执行语句	执行次数
int i=0;	4字节
int j=arr.length-1;	4字节
int m= (i+j)>>>1;	4字节
二分查找占用空间复杂度为：	O(1)

性能分析：

        时间复杂度：

                最坏情况：O(log(n))。

                最好情况：待查找元素在数组中央，O(1)。

        空间复杂度：需要常熟个数指针：i，j，m，额外占用空间是O(1)。

1.5 二分查找改进

在之前的二分查找算法中，如果数据在数组的最左侧，只需要执行L次 if 就可以了，但是如果数组在最右侧，那么需要执行L次 if 以及L次 else if，所以二分查找向左寻找元素，比向右寻找元素效率要高。

（1）左闭右开的区间，i指向的可能是目标，而j指向的不是目标。

（2）不在循环内找出，等范围内只剩下i时，退出循环，再循环外比较arr[i]与target。

（3）优点：循环内的平均比较次数减少了。

（4）缺点：时间复杂度：θ(log(n))。

1.6 二分查找相同元素

1.6.1 返回最左侧

当有两个数据相同时，上方的二分查找只会返回中间的元素，而我们想得到最左侧元素就需要对算法进行改进。（Leftmost）

 public static void main(String[] args) {int[] arr = {1, 22, 33, 55, 99, 99, 99, 366, 445, 999};System.out.println(binarySearchLeftMost1(arr, 99));//结果：4System.out.println(binarySearchLeftMost1(arr, 999));//结果：9System.out.println(binarySearchLeftMost1(arr, 998));//结果：-1}/*** @return int 找到相同元素返回返回最左侧查找元素索引，找不到返回-1* @Description 二分查找LeftMost* @Author LY* @Param [arr, target] 待查找升序数组，查找的值* @Date 2023/12/8 16:38**/public static int binarySearchLeftMost1(int[] arr, int target) {int i = 0;int j = arr.length - 1;int candidate = -1;while (i <= j) {int m = (i + j) >>> 1;if (target < arr[m]) {j = m - 1;} else if (arr[m] < target) {i = m + 1;} else {
//                return m;  查找到之后记录下来candidate=m;j=m-1;}}return candidate;}

1.6.2 返回最右侧

当有两个数据相同时，上方的二分查找只会返回中间的元素，而我们想得到最右侧元素就需要对算法进行改进。（Rightmost）

​public static void main(String[] args) {int[] arr = {1, 22, 33, 55, 99, 99, 99, 366, 445, 999};System.out.println(binarySearchRightMost1(arr, 99));//结果：6System.out.println(binarySearchRightMost1(arr, 999));//结果：9System.out.println(binarySearchRightMost1(arr, 998));//结果：-1}/*** @return int 找到相同元素返回返回最右侧侧查找元素索引，找不到返回-1* @Description 二分查找RightMost* @Author LY* @Param [arr, target] 待查找升序数组，查找的值* @Date 2023/12/8 16:38**/public static int binarySearchRightMost1(int[] arr, int target) {int i = 0;int j = arr.length - 1;int candidate = -1;while (i <= j) {int m = (i + j) >>> 1;if (target < arr[m]) {j = m - 1;} else if (arr[m] < target) {i = m + 1;} else {
//                return m;  查找到之后记录下来candidate=m;i = m + 1;}}return candidate;}​

1.6.3 优化

将leftMost优化后，可以在未找到目标值的情况下，返回大于等于目标值最靠左的一个索引。

/*** @return int 找到相同元素返回返回最左侧查找元素索引，找不到返回i* @Description 二分查找LeftMost* @Author LY* @Param [arr, target] 待查找升序数组，查找的值* @Date 2023/12/8 16:38**/public static int binarySearchLeftMost2(int[] arr, int target) {int i = 0;int j = arr.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target <= arr[m]) {j = m - 1;} else {i = m + 1;}}return i;}

将rightMost优化后，可以在未找到目标值的情况下，返回小于等于目标值最靠右的一个索引。

1.6.4 应用场景

1.6.4.1 查排名

（1）查找排名：
        在执行二分查找时，除了返回目标值是否存在于数组中，还可以记录查找过程中遇到的目标值的位置。如果找到了目标值，则直接返回该位置作为排名；如果没有找到目标值，但知道它应该插入到哪个位置才能保持数组有序，则可以返回这个位置作为排名。

         leftMost(target)+1
（2）查找前任（前驱）：
        如果目标值在数组中存在，并且不是数组的第一个元素，那么其前任就是目标值左边的一个元素。我们可以在找到目标值之后，再调用一次二分查找函数，这次查找的目标值设置为比当前目标值小一点的数。这样就可以找到目标值左侧最接近它的元素，即前任。

         leftMost(target)-1
（3）查找后任（后继）：
        如果目标值在数组中存在，并且不是数组的最后一个元素，那么其后任就是目标值右边的一个元素。类似地，我们可以在找到目标值之后，再调用一次二分查找函数，这次查找的目标值设置为比当前目标值大一点的数。这样就可以找到目标值右侧最接近它的元素，即后任。

         rightMost(target)+1

（3）最近邻居：

        前任和后任中，最接近目标值的一个元素。

1.6.4.2 条件查找元素

（1）小于某个值：0 ~ leftMost(target)-1

（2）小于等于某个值：0 ~ rightMost(target)

（3）大于某个值：rightMost(target)+1 ~ 无穷大

（4）大于等于某个值：leftMost(4) ~ 无穷大

（5）他们可以组合使用。