1. FFT理论相关知识
FFT(快速傅里叶变换)其本质就是DFT,只不过可以快速的计算出DFT结果,所以首先应该理解DFT,DFT(Discrete Fourier Transform) 离散傅里叶变换的缩写,FFT(Fast Fourier Transform)快速傅里叶变换的缩写,搞明白DFT之后,FFT就相对容易了。DFT(FFT)的作用是可以将信号从时域变换到频域,而且时域和频域都是离散的,通俗的说,可以求出一个信号由哪些正弦波叠加而成,求出的结果就是这些正弦波的幅度和相位.
1 .1 DFT
如图6-1所示,离散傅里叶变换可以将一个N点的输入信号变成两个N/2+1点的输出信号。输入信号含有已被分解的信号,而两个输出信号包含正弦波和余弦波的幅值信息。在时域x[ ]包含从0到N-l计N个样点。经过DFT变换之后,在频域产生两个信号:
其实部记作ReX[],虚部记作ImX[ ]。DFT变换是从时域变换到频域,而DFT逆变换与此相反,是从频域变换到时域.
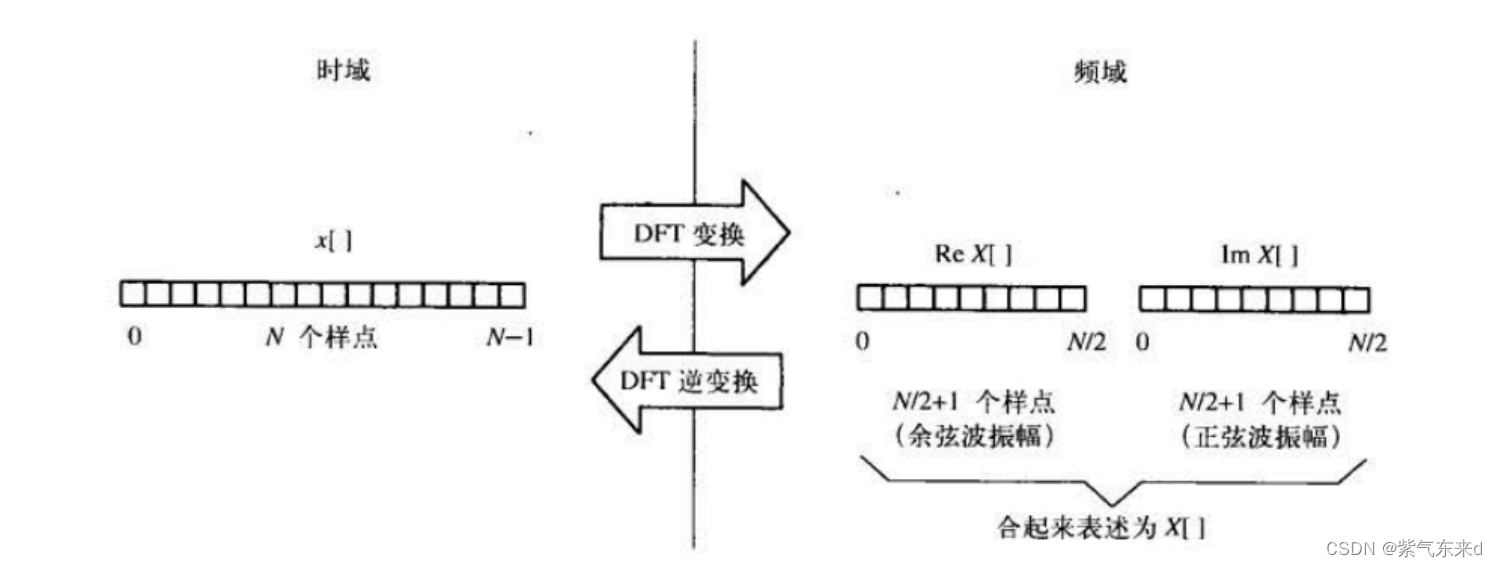
图6-1 实DFT变换
频域与时域描述的都是同一个信号,只是表述形式不同。如果已知其中的一个域,就能计算出另外一个域。通过给定的时域信号计算频域信号的过程就叫做分解、分析、正向DFT,或者简称为DFT。而通过给定的频域信号计算时域信号的过程就被称做合成或逆向DFT。无论分解还是合成都可以用方程式和计算机算法来描述。
时域的样点数常用变量N表示。虽然N可以是任意的正整数,但是通常选择2的k次方(k任意正整数),也就是128、256、512、1024等。这样选择的原因有以下两点:首先,数字数据存储使用二进制寻址方式,因此,2的k次方构成了一个信号的合理长度;其次,快速傅里叶变换(FFT)是计算DFT最有效的算法,它通常用N(N是2的k次方)进行运算。通常情况下,N值选在32和4096之间。在大多数的情况下,抽样序号是从0到N-1,而不是1到N。
DFT的标准算法——通过相关性计算 DFT。通过举例来说明此方法如何使用。假设我们现在要对一个64点的信号进行DFT计算,这意味着我们需要计算频域里实部的33个点和虚部的33个点。在这个例子中,我们只介绍如何计算单个样点的值,如ImX[3],即为从0点到63点之间含有3个完整周期的正弦波的幅值。同理可求得其余的频域值。
图6-2描述了如何使用相关性来计算ImX[3]。图6-2a和图6-2b是两个时域信号。
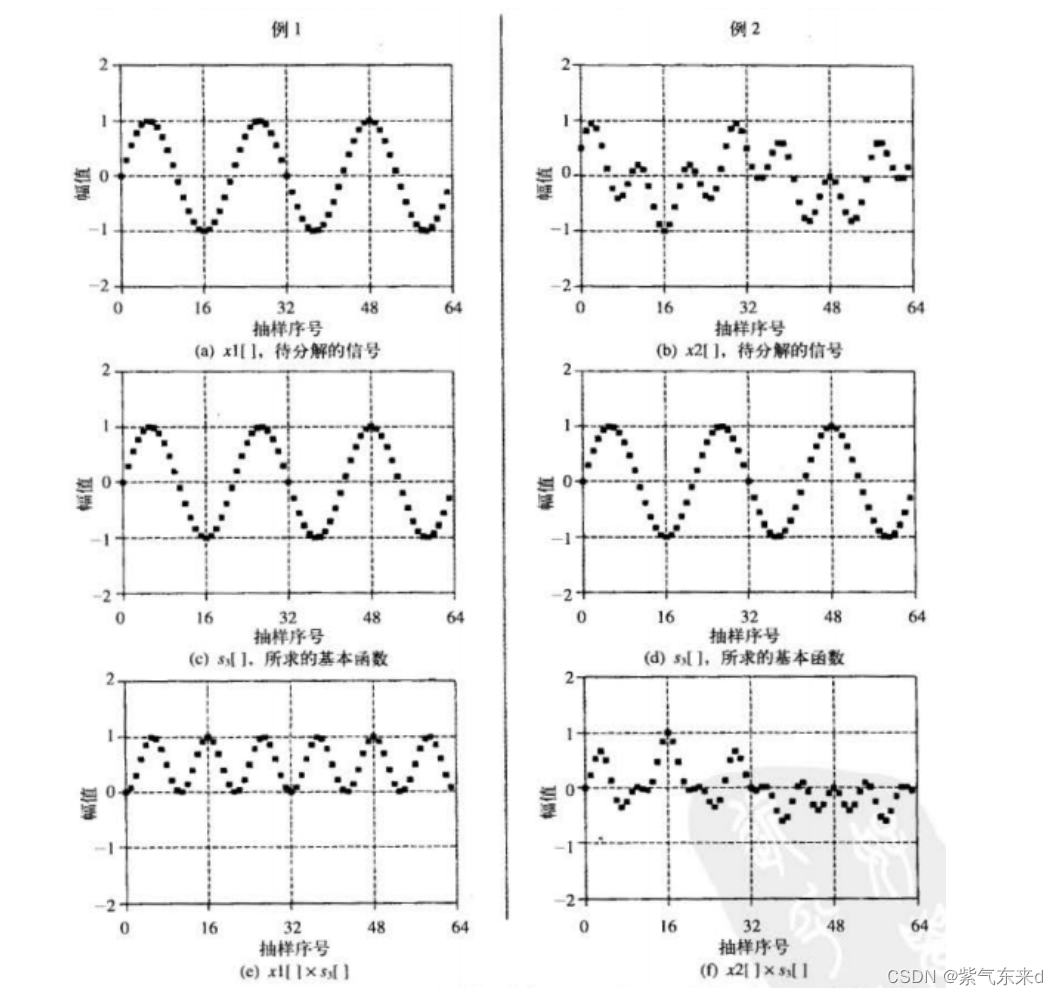
图6-2 通过相关性计算 ImX[3]
DFT的公式:
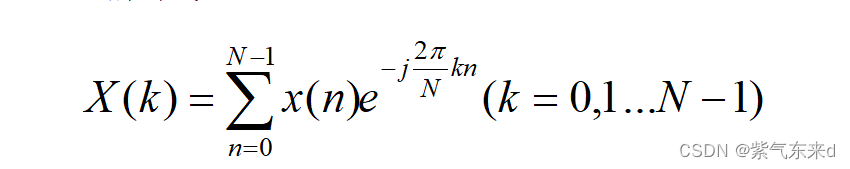
(6-1)
利用欧拉公式展开:
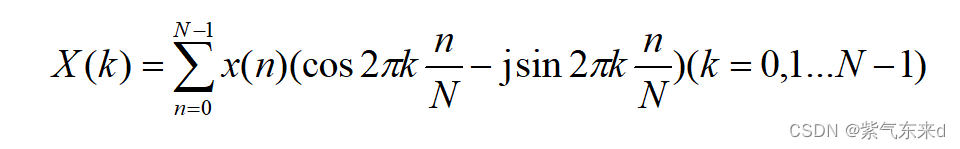
(6-2)
在计算机中可以这样展开:

(6-3)
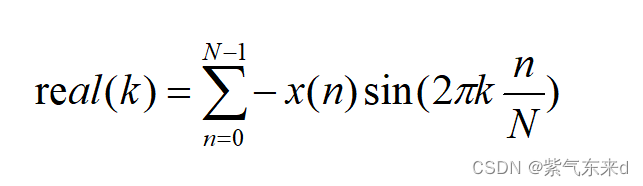
(6-4)
在python中实现的算法:
def DFT(Y,N):real = { }imag = { }ret = { }for k in range(N):real[k] = 0imag[k] = 0print(k)for n in range(N):real[k] = real[k] + Y[n] * np.cos(2 * np.pi * k * n / N)imag[k] = imag[k] - Y[n] * np.sin(2 * np.pi * k * n / N)ret[k] = np.sqrt( real[k]**2+imag[k]**2)return ret以上算法能够实现DFT功能了,从程序可以看出,该算法的时间复杂度是,在计算机中执行的速度太慢。所以接下来介绍比较快的算法FFT(快速傅里叶变换)。
1 .2 FFT
FFT变换首先把一个N点时域信号分解成N个时域信号,其中每个信号只包含一个点。第二步是计算出这N个时域信号相对应的N个频谱。最后,由这N个频谱合成一个频谱。如图6-3所示。FFT 分解。 一个 N 点信号被分解为 N个单点信号。每一步都使用交错分解,把偶数点和奇数点分开,如图6-4所示。

图1-3 FFT算法流程图

图1-4 FFT分解案例
FFT的最后一步是将N个频谱按照时域分解时重新排列的顺序进行组合。这就是此算法相对麻烦的地方。在第一步,8个频谱(每个频谱包含1点)被合成为4频谱(每个频谱包含2点),在第二步,4个频谱(每个频谱包含2点)被合成为2频谱(每个频谱包含4点),最后一步使得FFT的输出是一个8点的频谱。如图6-5所示。图6-6 是FFT运算的最基本元素,将两个复数点转换成另外两个复数点。

图1-5 FFT N=8点合成

图1-6 FFT蝶形运算最基本元素
1 .3 窗函数
如果连续时间信号 Xa(t) 在时域无限长,则离散化后的序列 X(n) 也是无限长的,而 DFT 只适用于有限长序列的计算,因此需要对 X(n) 加窗截断,使之成为有限长序列 XN(n),这个过程称为时域加窗(time-windowing)。设窗函数为Wn(N),则

(1-5)
有DFT的性质,时域上有两个序列相乘,在频域上是两个序列的离散时间傅里叶变换的卷积。
图1-7 原始信号

图1-8 窗函数

图1-9 加窗后的信号
使用不同的时间窗,它的时域形状和频域特征是不相同的。在这,介绍三种常见的窗函数的时域表达形式,以及它们的时域窗形状和频域特征。这三种窗分别是矩形窗、汉宁窗和平顶窗。它们的时域表达形式如下表所示,并且假设时间窗的范围为0≤t≤T,如果时间t的取值区间不同,窗函数的表达形式也会略有差异。

图1-10 几种窗函数
矩形窗、汉宁窗和平顶窗的时域形状和频域特征如下图所示,可以看出,窗函数不同,时域和频域都是不同的。

图1-11 几种窗函数的时域形状和频域特征
为了减少泄漏,可采用不同的窗函数来进行信号截取,因而,泄漏与窗函数的频谱特征相关的。窗函数的典型频谱特征如下图所示:
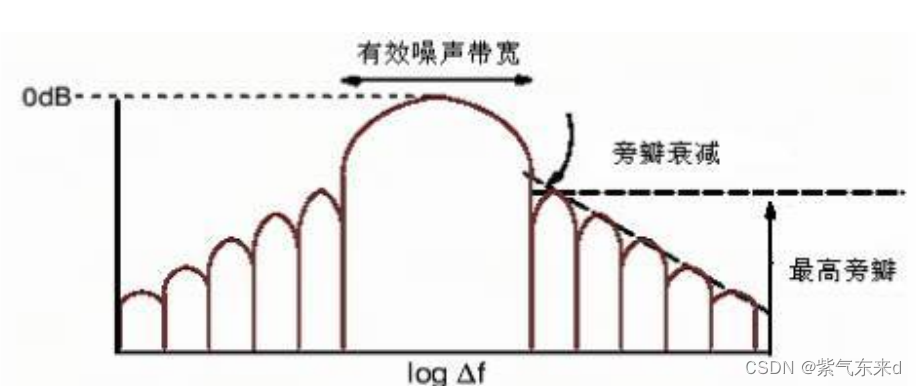
图1-12 几窗函数的典型频谱特征
代码请参考 一下代码在很多实际工程中用过,C语言实现快速傅立叶(FFT)(二)-CSDN博客



)














:弹幕列表)
