STL中sort的底层实现

文章目录

1、源码分析
2、算法优化
3、总结

在讲解STL中sort的底层原理之前，先引申出这样几个问题？

①STL中sort的底层是采用哪种或者哪几种排序？
②STL中sort会导致栈溢出吗？
③快速排序的时间复杂度是不稳定的 $log_2n$ ，最坏情况会变为n²，如何解决？
④STL中sort是如何控制递归深度的，如果已经到达了递归的深度，此时还没排完序该怎么办？

1、源码分析

C++STL中的sort默认会给我们提供两个接口，如下：

template <class RandomAccessIterator> void sort (RandomAccessIterator first, RandomAccessIterator last)
template <class RandomAccessIterator, class Compare> void sort (RandomAccessIterator first, RandomAccessIterator last, Compare comp)

第一个函数，有两个参数，分别表示迭代器的起始位置，和结束位置，它俩之间就是需要排序的区间

第二个函数，多了一个参数Compare comp，它比较的方式，可以是一个普通函数，或者是仿函数，或者是lambda表达式

如果我们不指定比较方式，默认采用升序排序

以下是vs2017的sort的源码，位置在\include\algorithm中

const int _ISORT_MAX = 32;	// maximum size for insertion sorttemplate<class _RanIt,class _Pr> inlinevoid _Sort_unchecked(_RanIt _First, _RanIt _Last, _Iter_diff_t<_RanIt> _Ideal, _Pr _Pred){	// order [_First, _Last), using _Pred_Iter_diff_t<_RanIt> _Count;while (_ISORT_MAX < (_Count = _Last - _First) && 0 < _Ideal){	// divide and conquer by quicksortauto _Mid = _Partition_by_median_guess_unchecked(_First, _Last, _Pred);// TRANSITION, VSO#433486_Ideal = (_Ideal >> 1) + (_Ideal >> 2);	// allow 1.5 log2(N) divisionsif (_Mid.first - _First < _Last - _Mid.second){	// loop on second half_Sort_unchecked(_First, _Mid.first, _Ideal, _Pred);_First = _Mid.second;}else{	// loop on first half_Sort_unchecked(_Mid.second, _Last, _Ideal, _Pred);_Last = _Mid.first;}}if (_ISORT_MAX < _Count){	// heap sort if too many divisions_Make_heap_unchecked(_First, _Last, _Pred);_Sort_heap_unchecked(_First, _Last, _Pred);}else if (2 <= _Count){_Insertion_sort_unchecked(_First, _Last, _Pred);	// small}}template<class _RanIt,class _Pr> inlinevoid sort(const _RanIt _First, const _RanIt _Last, _Pr _Pred){	// order [_First, _Last), using _Pred_Adl_verify_range(_First, _Last);  //用于检查区间的合法性const auto _UFirst = _Get_unwrapped(_First);const auto _ULast = _Get_unwrapped(_Last);_Sort_unchecked(_UFirst, _ULast, _ULast - _UFirst, _Pass_fn(_Pred));}template<class _RanIt> inlinevoid sort(const _RanIt _First, const _RanIt _Last){	// order [_First, _Last), using operator<_STD sort(_First, _Last, less<>());}

我们在调用sort时(没有传入第三个参数)，在algorithm中会去调用sort(const _RanIt _First, const _RanIt _Last)，在内部会调用sort(const _RanIt _First, const _RanIt _Last, _Pr _Pred)，进而会去调用_Sort_unchecked(_RanIt _First, _RanIt _Last, _Iter_diff_t<_RanIt> _Ideal, _Pr _Pred)

因此，主要调用的就是_Sort_unchecked函数：

void _Sort_unchecked(_RanIt _First, _RanIt _Last, _Iter_diff_t<_RanIt> _Ideal, _Pr _Pred)

_First：首元素的迭代器
_Last：末尾元素下一个位置的迭代器
_Ideal：递归层数
_Pred：指定的排序方式

在_Sort_unchecked函数中，如果需要排序的元素是否大于_ISORT_MAX(32)并且递归深度大于0，就进入while循环，通过_Partition_by_median_guess_unchecked函数选取一个mid，然后更新当前排序元素个数的递归深度，接着会递归调用_Sort_unchecked函数。

如果没有进入while循环，就说明但当前排序的元素个数小于等于_ISORT_MAX(32)，或者递归深度小于等于0，接着就判断当前排序的元素个数是否大于_ISORT_MAX(32)，如果是则说明递归深度小于等于0，因此就采用堆排序来控制递归深度

如果上述条件都没满足，则说明需要排序的元素小于等于32，大于2，此时采用插入排序来进行优化

递归的深度通过以下方式来控制，每次递归，递归的深度都会通过以下方式减少

_Ideal = (_Ideal >> 1) + (_Ideal >> 2);	// allow 1.5 log2(N) divisions

最多允许递归1.5*log2(N)层，比如需要排序的元素为1024，那么1.5*log2(1024)=15层，因此最多递归15层，如果需要排序的元素为512，那么最多递归8层

2、算法优化

在这里就不再过多赘述快排的原理，如果还有不知道的小伙伴，就看看我以往写的博客快速排序

因为快排需要选一个基准值用于比较，如果只是单纯的选择最左边的值或者选择最右边的，当将一个有序数列进行反向排序时(升序改为降序，降序改为升序)，那么时间复杂度必然为n²，为了防止这个问题，在_Guess_median_unchecked函数内还进行了优化，优化的方式就是三数取中

auto _Mid = _Partition_by_median_guess_unchecked(_First, _Last, _Pred);

template<class _RanIt,class _Pr> inlinepair<_RanIt, _RanIt>_Partition_by_median_guess_unchecked(_RanIt _First, _RanIt _Last, _Pr _Pred){	// partition [_First, _Last), using _Pred//这里取了一个中间值，但是在_Guess_median_unchecked内部会对该位置的数据进行优化_RanIt _Mid = _First + ((_Last - _First) >> 1);	// TRANSITION, VSO#433486_Guess_median_unchecked(_First, _Mid, _Last - 1, _Pred);_RanIt _Pfirst = _Mid;_RanIt _Plast = _Pfirst + 1;while (_First < _Pfirst&& !_DEBUG_LT_PRED(_Pred, *(_Pfirst - 1), *_Pfirst)&& !_Pred(*_Pfirst, *(_Pfirst - 1))){--_Pfirst;}while (_Plast < _Last&& !_DEBUG_LT_PRED(_Pred, *_Plast, *_Pfirst)&& !_Pred(*_Pfirst, *_Plast)){++_Plast;}_RanIt _Gfirst = _Plast;_RanIt _Glast = _Pfirst;for (;;){	// partitionfor (; _Gfirst < _Last; ++_Gfirst){if (_DEBUG_LT_PRED(_Pred, *_Pfirst, *_Gfirst)){}else if (_Pred(*_Gfirst, *_Pfirst)){break;}else if (_Plast != _Gfirst){_STD iter_swap(_Plast, _Gfirst);++_Plast;}else{++_Plast;}}for (; _First < _Glast; --_Glast){if (_DEBUG_LT_PRED(_Pred, *(_Glast - 1), *_Pfirst)){}else if (_Pred(*_Pfirst, *(_Glast - 1))){break;}else if (--_Pfirst != _Glast - 1){_STD iter_swap(_Pfirst, _Glast - 1);}}if (_Glast == _First && _Gfirst == _Last){return (pair<_RanIt, _RanIt>(_Pfirst, _Plast));}if (_Glast == _First){	// no room at bottom, rotate pivot upwardif (_Plast != _Gfirst){_STD iter_swap(_Pfirst, _Plast);}++_Plast;_STD iter_swap(_Pfirst, _Gfirst);++_Pfirst;++_Gfirst;}else if (_Gfirst == _Last){	// no room at top, rotate pivot downwardif (--_Glast != --_Pfirst){_STD iter_swap(_Glast, _Pfirst);}_STD iter_swap(_Pfirst, --_Plast);}else{_STD iter_swap(_Gfirst, --_Glast);++_Gfirst;}}}

这个Mid会返回两个值，[Mid.first，Mid.second]范围内是等于基准值的

选择基准值时，还调用函数_Guess_median_unchecked进行了优化，这个函数就是三数取中

template<class _RanIt,class _Pr> inlinevoid _Guess_median_unchecked(_RanIt _First, _RanIt _Mid, _RanIt _Last, _Pr _Pred){	// sort median element to middleusing _Diff = _Iter_diff_t<_RanIt>;const _Diff _Count = _Last - _First;if (40 < _Count){	// median of nineconst _Diff _Step = (_Count + 1) >> 3; // +1 can't overflow because range was made inclusive in callerconst _Diff _Two_step = _Step << 1; // note: intentionally discards low-order bit_Med3_unchecked(_First, _First + _Step, _First + _Two_step, _Pred);_Med3_unchecked(_Mid - _Step, _Mid, _Mid + _Step, _Pred);_Med3_unchecked(_Last - _Two_step, _Last - _Step, _Last, _Pred);_Med3_unchecked(_First + _Step, _Mid, _Last - _Step, _Pred);}else{_Med3_unchecked(_First, _Mid, _Last, _Pred);}}

这里首先会判断需要排序的元素个数_Count = _Last - _First如果大于40个，则会在if内部定义两个变量，_Step 和 _Two_step，分别表示从区间的起始位置开始的1/8位置处和1/4位置处，此时就有9个位置，_First，_First + _Step，_First + _Two_step，_Mid - _Step，_Mid，_Mid + _Step，_Last - _Two_step，_Last - _Step，_Last。如图所示：

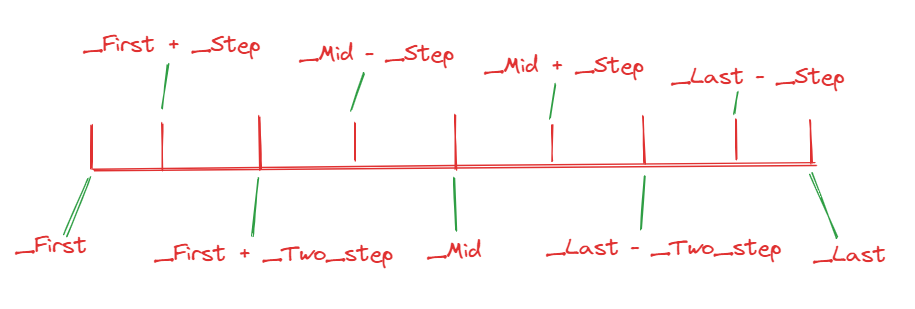
在这里插入图片描述

接着通过4组_Med3_unchecked函数，将该9个位置的数据，按照特定的排序规则排序(升序或者降序)

如果需要排序的元素个数大于40，则只需_Last，_Mid 和 _Last 位置所在的数据按照特定的排序规则排序(升序或者降序)

_Med3_unchecked函数

template<class _RanIt,class _Pr> inlinevoid _Med3_unchecked(_RanIt _First, _RanIt _Mid, _RanIt _Last, _Pr _Pred){	// sort median of three elements to middleif (_DEBUG_LT_PRED(_Pred, *_Mid, *_First)){_STD iter_swap(_Mid, _First);}if (_DEBUG_LT_PRED(_Pred, *_Last, *_Mid)){	// swap middle and last, then test first again_STD iter_swap(_Last, _Mid);if (_DEBUG_LT_PRED(_Pred, *_Mid, *_First)){_STD iter_swap(_Mid, _First);}}}

_DEBUG_LT_PRED这个宏的作用就是判断后两个参数，也就是位置所对应的数据是否按照特定的排序方式(_Pred)排序，如果不是的话，就通过iter_swap交换

通过_Guess_median_unchecked(_First, _Mid, _Last - 1, _Pred)这个函数，我们已经取得mid基准值，并且mid位置的数据一定大于等于_First，并且小于等于_Last - 1

接着会定义 _Pfirst 和 _Plast

_RanIt _Pfirst = _Mid;
_RanIt _Plast = _Pfirst + 1;

此时的位置关系图如下：

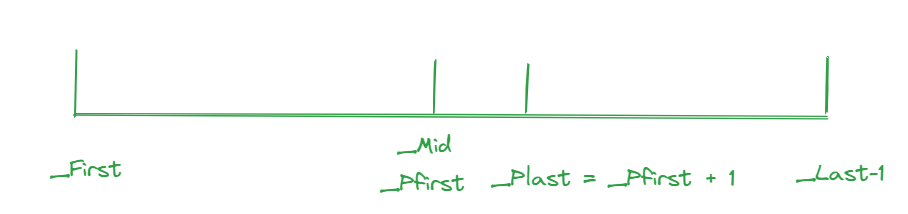
在这里插入图片描述

后面两个while是用来选等于基准值的数，最后_Pfirst的处等于基准值，而_Pfirst + 1一定不等于基准值

接着会定义_Gfirst 和 _Glast

_RanIt _Gfirst = _Plast;
_RanIt _Glast = _Pfirst;

位置关系如下：

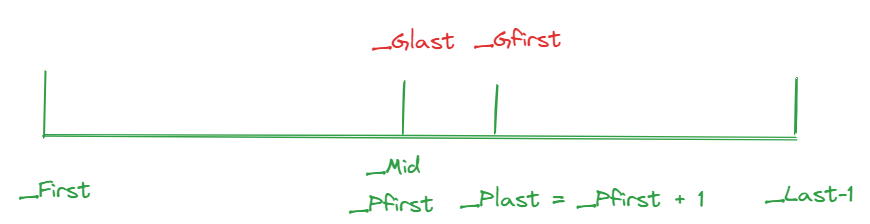
在这里插入图片描述

下面的两个for循环就是分别是_Gfirst出发向右走，_Glast出发向左走，以_Gfirst为例子，如果遇到大于基准值(_Pfirst)那么进行下一轮循环，如果小于，那么break，然后在下面和_Glast交换，如果是相等那么和_Plast交换并更新

3、总结

①STL中sort的底层是采用哪种或者哪几种排序？

采用三种排序
如果元素的个数小于等于32，那么就直接使用插入排序

如果元素的个数大于32，但是已经达到最大的递归深度，则采用堆排序
这里为什么采用堆排序，而不采用归并排序呢？因为堆排序不需要消耗额外的空间

如果元素的个数大于32，但还没达到最大的递归深度，则采用快速排序

STL中sort会导致栈溢出吗？

不会，因为对最大的递归深度做了限制，最大的深度不能超过1.5*log2(N)层

③快速排序的时间复杂度是不稳定的 $log_2n$ ，最坏情况会变为n²，如何解决？

sort快排进行了优化，即对基准值做了优化，如果基准值恰好是最大或者最小值那么快排的复杂度会达到n²，因此需要选择一个适中的基准值。如果元素个数大于40个，那么会将整个区间划分为8段，9个位置，对这个9个位置的数据进行排序，最终取出mid。如果元素个数小于等于40个，那么会将整个区间划分为2段，3个位置，对这个3个位置的数据进行排序，最终取出mid。

④STL中sort是如何控制递归深度的，如果已经到达了递归的深度，此时还没排完序该怎么办？

通过这行代码控制递归深度

_Ideal = (_Ideal >> 1) + (_Ideal >> 2);	// allow 1.5 log2(N) divisions

最大的深度不能超过1.5*log2(N)层，如果超过了最大递归深度，则采用堆排序